Euclidische algoritmen (basis en uitgebreid)
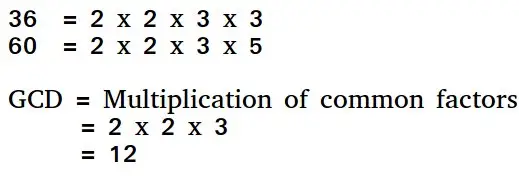
Het Euclidische algoritme is een manier om de grootste gemene deler van twee positieve gehele getallen te vinden. GCD van twee getallen is het grootste getal dat beide getallen deelt. Een eenvoudige manier om GCD te vinden is door beide getallen te ontbinden en gemeenschappelijke priemfactoren te vermenigvuldigen.
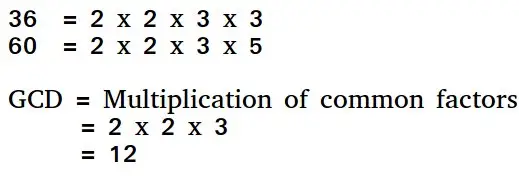
Basis Euclidisch algoritme voor GCD:
Het algoritme is gebaseerd op de onderstaande feiten.
- Als we een kleiner getal aftrekken van een groter getal (we verkleinen een groter getal), verandert GCD niet. Dus als we herhaaldelijk de grootste van twee aftrekken, eindigen we met GCD.
- Als we nu in plaats van aftrekken het kleinere getal delen, stopt het algoritme wanneer we de rest 0 vinden.
Hieronder staat een recursieve functie om ggd te evalueren met behulp van het algoritme van Euclides:
C
// C program to demonstrate Basic Euclidean Algorithm> #include> // Function to return gcd of a and b> int> gcd(> int> a,> int> b)> {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> }> // Driver code> int> main()> {> > int> a = 10, b = 15;> > > // Function call> > printf> (> 'GCD(%d, %d) = %d
'> , a, b, gcd(a, b));> > a = 35, b = 10;> > printf> (> 'GCD(%d, %d) = %d
'> , a, b, gcd(a, b));> > a = 31, b = 2;> > printf> (> 'GCD(%d, %d) = %d
'> , a, b, gcd(a, b));> > return> 0;> }> |
CPP
// C++ program to demonstrate> // Basic Euclidean Algorithm> #include> using> namespace> std;> // Function to return> // gcd of a and b> int> gcd(> int> a,> int> b)> {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> }> // Driver Code> int> main()> {> > int> a = 10, b = 15;> > > // Function call> > cout < <> 'GCD('> < < a < <> ', '> < < b < <> ') = '> < < gcd(a, b)> > < < endl;> > a = 35, b = 10;> > cout < <> 'GCD('> < < a < <> ', '> < < b < <> ') = '> < < gcd(a, b)> > < < endl;> > a = 31, b = 2;> > cout < <> 'GCD('> < < a < <> ', '> < < b < <> ') = '> < < gcd(a, b)> > < < endl;> > return> 0;> }> |
Java
// Java program to demonstrate Basic Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> > // extended Euclidean Algorithm> > public> static> int> gcd(> int> a,> int> b)> > {> > if> (a ==> 0> )> > return> b;> > return> gcd(b % a, a);> > }> > // Driver code> > public> static> void> main(String[] args)> > {> > int> a => 10> , b => 15> , g;> > > // Function call> > g = gcd(a, b);> > System.out.println(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a => 35> ;> > b => 10> ;> > g = gcd(a, b);> > System.out.println(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a => 31> ;> > b => 2> ;> > g = gcd(a, b);> > System.out.println(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > }> }> // Code Contributed by Mohit Gupta_OMG> |
Python3
# Python3 program to demonstrate Basic Euclidean Algorithm> # Function to return gcd of a and b> def> gcd(a, b):> > if> a> => => 0> :> > return> b> > return> gcd(b> %> a, a)> # Driver code> if> __name__> => => '__main__'> :> > a> => 10> > b> => 15> > print> (> 'gcd('> , a,> ','> , b,> ') = '> , gcd(a, b))> > a> => 35> > b> => 10> > print> (> 'gcd('> , a,> ','> , b,> ') = '> , gcd(a, b))> > a> => 31> > b> => 2> > print> (> 'gcd('> , a,> ','> , b,> ') = '> , gcd(a, b))> # Code Contributed By Mohit Gupta_OMG> |
C#
// C# program to demonstrate Basic Euclidean Algorithm> using> System;> class> GFG {> > public> static> int> gcd(> int> a,> int> b)> > {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> > }> > // Driver Code> > static> public> void> Main()> > {> > int> a = 10, b = 15, g;> > g = gcd(a, b);> > Console.WriteLine(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a = 35;> > b = 10;> > g = gcd(a, b);> > Console.WriteLine(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a = 31;> > b = 2;> > g = gcd(a, b);> > Console.WriteLine(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > }> }> // This code is contributed by ajit> |
PHP
// php program to demonstrate Basic Euclidean Algorithm> // PHP program to demonstrate // Basic Euclidean Algorithm // Function to return // gcd of a and b function gcd($a, $b) { if ($a == 0) return $b; return gcd($b % $a, $a); } // Driver Code $a = 10; $b = 15; // Function call echo 'GCD(',$a,',' , $b,') = ', gcd($a, $b); echo '
'; $a = 35; $b = 10; echo 'GCD(',$a ,',',$b,') = ', gcd($a, $b); echo '
'; $a = 31; $b = 2; echo 'GCD(',$a ,',', $b,') = ', gcd($a, $b); // This code is contributed by m_kit ?>> |
Javascript
// JavaScript program to demonstrate> // Basic Euclidean Algorithm> // Function to return> // gcd of a and b> function> gcd( a, b)> {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> }> // Driver Code> > let a = 10, b = 15;> > document.write(> 'GCD('> + a +> ', '> > + b +> ') = '> + gcd(a, b) +> ' '> );> > > a = 35, b = 10;> > document.write(> 'GCD('> + a +> ', '> > + b +> ') = '> + gcd(a, b) +> ' '> );> > > a = 31, b = 2;> > document.write(> 'GCD('> + a +> ', '> > + b +> ') = '> + gcd(a, b) +> ' '> );> // This code contributed by aashish1995> |
Uitvoer
GCD(10, 15) = 5 GCD(35, 10) = 5 GCD(31, 2) = 1
Tijdcomplexiteit: O(Logmin(a, b))
Hulpruimte: O(Logboek (min(a,b))
Uitgebreid Euclidisch algoritme:
Uitgebreid Euclidisch algoritme vindt ook gehele coëfficiënten x en y zodat: ax + by = ggd(a, b)
Voorbeelden:
Invoer: a = 30, b = 20
Uitgang: ggd = 10, x = 1, y = -1
(Merk op dat 30*1 + 20*(-1) = 10)Invoer: a = 35, b = 15
Uitgang: ggd = 5, x = 1, y = -2
(Merk op dat 35*1 + 15*(-2) = 5)
Het uitgebreide Euclidische algoritme werkt de resultaten van ggd(a, b) bij met behulp van de resultaten berekend door de recursieve aanroep ggd(b%a, a). Laat de waarden van x en y, berekend door de recursieve aanroep, x zijn 1 en j 1 . x en y worden bijgewerkt met behulp van de onderstaande expressies.
Aanbevolen praktijk Uitgebreid Euclidisch algoritme Probeer het!bijl + door = ggd(a, b)
ggd(a, b) = ggd(b%a, a)
ggd(b%a, a) = (b%a)x 1 + is 1
bijl + door = (b%a)x 1 + is 1
bijl + door = (b – [b/a] * a)x 1 + is 1
bijl + door = a(j 1 – [b/a] * x 1 ) + bx 1Vergelijking van LHS en RHS,
x = y 1 – ?b/a? * X 1
y = x 1
Hieronder vindt u een implementatie van de bovenstaande aanpak:
C++
// C++ program to demonstrate working of> // extended Euclidean Algorithm> #include> using> namespace> std;> // Function for extended Euclidean Algorithm> int> gcdExtended(> int> a,> int> b,> int> *x,> int> *y)> {> > // Base Case> > if> (a == 0)> > {> > *x = 0;> > *y = 1;> > return> b;> > }> > int> x1, y1;> // To store results of recursive call> > int> gcd = gcdExtended(b%a, a, &x1, &y1);> > // Update x and y using results of> > // recursive call> > *x = y1 - (b/a) * x1;> > *y = x1;> > return> gcd;> }> // Driver Code> int> main()> {> > int> x, y, a = 35, b = 15;> > int> g = gcdExtended(a, b, &x, &y);> > cout < <> 'GCD('> < < a < <> ', '> < < b> > < <> ') = '> < < g < < endl;> > return> 0;> }> |
C
// C program to demonstrate working of extended> // Euclidean Algorithm> #include> // C function for extended Euclidean Algorithm> int> gcdExtended(> int> a,> int> b,> int> *x,> int> *y)> {> > // Base Case> > if> (a == 0)> > {> > *x = 0;> > *y = 1;> > return> b;> > }> > int> x1, y1;> // To store results of recursive call> > int> gcd = gcdExtended(b%a, a, &x1, &y1);> > // Update x and y using results of recursive> > // call> > *x = y1 - (b/a) * x1;> > *y = x1;> > return> gcd;> }> // Driver Program> int> main()> {> > int> x, y;> > int> a = 35, b = 15;> > int> g = gcdExtended(a, b, &x, &y);> > printf> (> 'gcd(%d, %d) = %d'> , a, b, g);> > return> 0;> }> |
Java
// Java program to demonstrate working of extended> // Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> > // extended Euclidean Algorithm> > public> static> int> gcdExtended(> int> a,> int> b,> int> x,> > int> y)> > {> > // Base Case> > if> (a ==> 0> ) {> > x => 0> ;> > y => 1> ;> > return> b;> > }> > int> x1 => 1> ,> > y1 => 1> ;> // To store results of recursive call> > int> gcd = gcdExtended(b % a, a, x1, y1);> > // Update x and y using results of recursive> > // call> > x = y1 - (b / a) * x1;> > y = x1;> > return> gcd;> > }> > // Driver Program> > public> static> void> main(String[] args)> > {> > int> x => 1> , y => 1> ;> > int> a => 35> , b => 15> ;> > int> g = gcdExtended(a, b, x, y);> > System.out.print(> 'gcd('> + a +> ' , '> + b> > +> ') = '> + g);> > }> }> |
Python3
# Python program to demonstrate working of extended> # Euclidean Algorithm> # function for extended Euclidean Algorithm> def> gcdExtended(a, b):> > # Base Case> > if> a> => => 0> :> > return> b,> 0> ,> 1> > gcd, x1, y1> => gcdExtended(b> %> a, a)> > # Update x and y using results of recursive> > # call> > x> => y1> -> (b> /> /> a)> *> x1> > y> => x1> > return> gcd, x, y> # Driver code> a, b> => 35> ,> 15> g, x, y> => gcdExtended(a, b)> print> (> 'gcd('> , a,> ','> , b,> ') = '> , g)> |
C#
// C# program to demonstrate working> // of extended Euclidean Algorithm> using> System;> class> GFG> {> > > // extended Euclidean Algorithm> > public> static> int> gcdExtended(> int> a,> int> b,> > int> x,> int> y)> > {> > // Base Case> > if> (a == 0)> > {> > x = 0;> > y = 1;> > return> b;> > }> > // To store results of> > // recursive call> > int> x1 = 1, y1 = 1;> > int> gcd = gcdExtended(b % a, a, x1, y1);> > // Update x and y using> > // results of recursive call> > x = y1 - (b / a) * x1;> > y = x1;> > return> gcd;> > }> > > // Driver Code> > static> public> void> Main ()> > {> > int> x = 1, y = 1;> > int> a = 35, b = 15;> > int> g = gcdExtended(a, b, x, y);> > Console.WriteLine(> 'gcd('> + a +> ' , '> +> > b +> ') = '> + g);> > }> }> |
PHP
// PHP program to demonstrate // working of extended // Euclidean Algorithm // PHP function for // extended Euclidean // Algorithm function gcdExtended($a, $b, $x, $y) { // Base Case if ($a == 0) { $x = 0; $y = 1; return $b; } // To store results // of recursive call $gcd = gcdExtended($b % $a, $a, $x, $y); // Update x and y using // results of recursive // call $x = $y - floor($b / $a) * $x; $y = $x; return $gcd; } // Driver Code $x = 0; $y = 0; $a = 35; $b = 15; $g = gcdExtended($a, $b, $x, $y); echo 'gcd(',$a; echo ', ' , $b, ')'; echo ' = ' , $g; ?>> |
Javascript
> // Javascript program to demonstrate> // working of extended> // Euclidean Algorithm> // Javascript function for> // extended Euclidean> // Algorithm> function> gcdExtended(a, b,> > x, y)> {> > // Base Case> > if> (a == 0)> > {> > x = 0;> > y = 1;> > return> b;> > }> > // To store results> > // of recursive call> > let gcd = gcdExtended(b % a,> > a, x, y);> > // Update x and y using> > // results of recursive> > // call> > x = y - (b / a) * x;> > y = x;> > return> gcd;> }> // Driver Code> let x = 0;> let y = 0;> let a = 35;> let b = 15;> let g = gcdExtended(a, b, x, y);> document.write(> 'gcd('> + a);> document.write(> ', '> + b +> ')'> );> document.write(> ' = '> + g);> > |
Uitgang:
gcd(35, 15) = 5
Tijdcomplexiteit: O(log N)
Hulpruimte: O(log N)
Hoe werkt het uitgebreide algoritme?
Zoals hierboven te zien zijn, zijn x en y resultaten voor invoer a en b,
a.x + b.y = ggd —-(1)
En x 1 en j 1 zijn resultaten voor invoer b%a en a
(b%a).x 1 + a.j 1 = gcd
Als we b%a = (b – (?b/a?).a) hierboven plaatsen,
wij krijgen navolging. Merk op dat ?b/a? is verdieping(b/a)(b – (?b/a?).a).x 1 + a.j 1 = gcd
Bovenstaande vergelijking kan ook worden geschreven zoals hieronder
b.x 1 + een.(en 1 – (?b/a?).x 1 ) = ggd —(2)
Na het vergelijken van de coëfficiënten van ‘a’ en ‘b’ in (1) en
(2), we krijgen het volgende,
x = y 1 – ?b/a? * X 1
y = x 1
Hoe is uitgebreid algoritme nuttig?
Het uitgebreide Euclidische algoritme is vooral handig wanneer a en b coprime zijn (of ggd is 1). Omdat x de modulaire multiplicatieve inverse is van a modulo b, en y de modulaire multiplicatieve inverse is van b modulo a. In het bijzonder is de berekening van de modulaire multiplicatieve inverse een essentiële stap in de RSA-encryptiemethode met publieke sleutels.