Segments minimum dans un affichage à sept segments
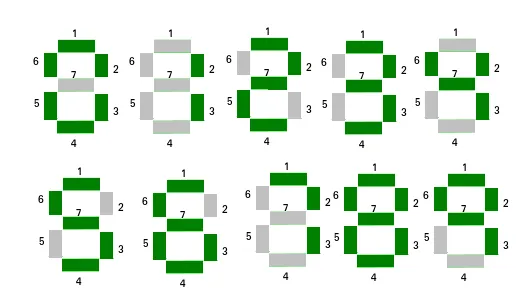
Un affichage à sept segments peut être utilisé pour afficher des chiffres. Étant donné un éventail de n nombres naturels. La tâche consiste à trouver le nombre dans le tableau qui utilise le nombre minimum de segments pour afficher le nombre. Si plusieurs nombres ont un nombre minimum de segments, le nombre ayant le plus petit index est affiché.

Exemples :
Saisir : arr[] = { 1 2 3 4 5 }.
Sortir : 1
Explication: L'élément qui utilise le nombre minimum de segments est 1 (c'est-à-dire 2 segments)Saisir : arr[] = { 489 206 745 123 756 }.
Sortir : 745
Explication: L'élément avec le plus petit indice qui utilise le nombre minimum de segments est 745 (soit 12 segments)
L'idée est de précalculer le nombre de segments utilisés par les chiffres de 0 à 9 et de le stocker. Maintenant, pour chaque élément du tableau, additionnez le nombre de segments utilisés par chaque chiffre. Recherchez ensuite l’élément qui utilise le nombre minimum de segments.
C++Le nombre de segments utilisés par chiffre :
0 -> 6
1 -> 2
2 -> 5
3 -> 5
4 -> 4
5 -> 5
6 -> 6
7 -> 3
8 -> 7
9 -> 6
#include using namespace std ; // Precomputed values of segment used by digit 0 to 9. const int seg [ 10 ] = { 6 2 5 5 4 5 6 3 7 6 }; // Return the number of segments used by x. int computeSegment ( int x ) { if ( x == 0 ) return seg [ 0 ]; int count = 0 ; // Finding sum of the segment used by // each digit of a number. while ( x ) { count += seg [ x % 10 ]; x /= 10 ; } return count ; } int elementMinSegment ( vector < int > arr int n ) { // Initialising the minimum segment and minimum // number index. int minseg = computeSegment ( arr [ 0 ]); int minindex = 0 ; // Finding and comparing segment used // by each number arr[i]. for ( int i = 1 ; i < n ; i ++ ) { int temp = computeSegment ( arr [ i ]); // If arr[i] used less segment then update // minimum segment and minimum number. if ( temp < minseg ) { minseg = temp ; minindex = i ; } } return arr [ minindex ]; } int main () { vector < int > arr = { 489 206 745 123 756 }; int n = arr . size (); cout < < elementMinSegment ( arr n ) < < endl ; return 0 ; }
Java import java.io.* ; class GFG { // Precomputed values of segment // used by digit 0 to 9. static int [] seg = { 6 2 5 5 4 5 6 3 7 6 }; // Return the number of segments used by x. static int computeSegment ( int x ) { if ( x == 0 ) return seg [ 0 ] ; int count = 0 ; // Finding sum of the segment used by // each digit of a number. while ( x > 0 ) { count += seg [ x % 10 ] ; x /= 10 ; } return count ; } static int elementMinSegment ( int [] arr int n ) { // Initialising the minimum segment // and minimum number index. int minseg = computeSegment ( arr [ 0 ] ); int minindex = 0 ; // Finding and comparing segment used // by each number arr[i]. for ( int i = 1 ; i < n ; i ++ ) { int temp = computeSegment ( arr [ i ] ); // If arr[i] used less segment then update // minimum segment and minimum number. if ( temp < minseg ) { minseg = temp ; minindex = i ; } } return arr [ minindex ] ; } static public void main ( String [] args ) { int [] arr = { 489 206 745 123 756 }; int n = arr . length ; System . out . println ( elementMinSegment ( arr n )); } }
Python # Precomputed values of segment # used by digit 0 to 9. seg = [ 6 2 5 5 4 5 6 3 7 6 ] # Return the number of # segments used by x. def computeSegment ( x ): if ( x == 0 ): return seg [ 0 ] count = 0 # Finding sum of the segment # used by each digit of a number. while ( x ): count += seg [ x % 10 ] x = x // 10 return count # function to return minimum sum index def elementMinSegment ( arr n ): # Initialising the minimum # segment and minimum number index. minseg = computeSegment ( arr [ 0 ]) minindex = 0 # Finding and comparing segment # used by each number arr[i]. for i in range ( 1 n ): temp = computeSegment ( arr [ i ]) # If arr[i] used less segment # then update minimum segment # and minimum number. if ( temp < minseg ): minseg = temp minindex = i return arr [ minindex ] # Driver Code arr = [ 489 206 745 123 756 ] n = len ( arr ) # function print required answer print ( elementMinSegment ( arr n )) # This code is contributed by # Sanjit_Prasad
C# using System ; class GFG { // Precomputed values of segment // used by digit 0 to 9. static int [] seg = new int [ 10 ]{ 6 2 5 5 4 5 6 3 7 6 }; // Return the number of segments used by x. static int computeSegment ( int x ) { if ( x == 0 ) return seg [ 0 ]; int count = 0 ; // Finding sum of the segment used by // each digit of a number. while ( x > 0 ) { count += seg [ x % 10 ]; x /= 10 ; } return count ; } static int elementMinSegment ( int [] arr int n ) { // Initialising the minimum segment // and minimum number index. int minseg = computeSegment ( arr [ 0 ]); int minindex = 0 ; // Finding and comparing segment used // by each number arr[i]. for ( int i = 1 ; i < n ; i ++ ) { int temp = computeSegment ( arr [ i ]); // If arr[i] used less segment then update // minimum segment and minimum number. if ( temp < minseg ) { minseg = temp ; minindex = i ; } } return arr [ minindex ]; } static public void Main () { int [] arr = { 489 206 745 123 756 }; int n = arr . Length ; Console . WriteLine ( elementMinSegment ( arr n )); } }
JavaScript // Precomputed values of segment // used by digit 0 to 9. let seg = [ 6 2 5 5 4 5 6 3 7 6 ]; // Return the number of segments used by x. function computeSegment ( x ) { if ( x == 0 ) return seg [ 0 ]; let count = 0 ; // Finding sum of the segment used by // each digit of a number. while ( x > 0 ) { count += seg [ x % 10 ]; x = parseInt ( x / 10 10 ); } return count ; } function elementMinSegment ( arr n ) { // Initialising the minimum segment // and minimum number index. let minseg = computeSegment ( arr [ 0 ]); let minindex = 0 ; // Finding and comparing segment used // by each number arr[i]. for ( let i = 1 ; i < n ; i ++ ) { let temp = computeSegment ( arr [ i ]); // If arr[i] used less segment then update // minimum segment and minimum number. if ( temp < minseg ) { minseg = temp ; minindex = i ; } } return arr [ minindex ]; } // Driver code let arr = [ 489 206 745 123 756 ]; let n = arr . length ; console . log ( elementMinSegment ( arr n ));
Sortir
745
Complexité temporelle : O(n * log 10 n)
Espace auxiliaire : O(10)


![Comment vérifier qui a consulté les faits saillants d'Instagram [2024]](https://techcodeview.com/img/how/24/how-check-who-viewed-instagram-highlights.webp)