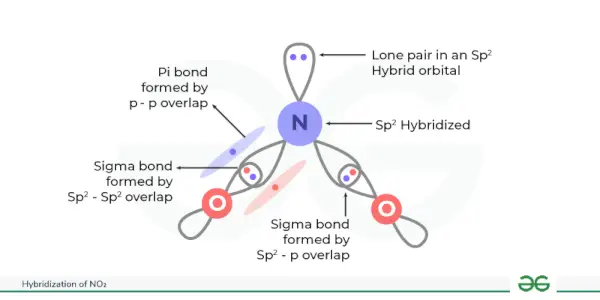
a ² – b ² formula iekšā Algebra ir matemātikas pamatformula, ko izmanto dažādu algebrisko problēmu risināšanai. a ² – b ² formulu sauc arī par kvadrātformulas atšķirību, jo šī formula palīdz mums atrast atšķirību starp diviem kvadrātiem, faktiski neaprēķinot kvadrātus. Tālāk pievienotajā attēlā parādīta a formula ² – b ²

Šajā rakstā mēs uzzināsim a ² – b ² formula, a ² – b ² identitāte, piemēri un citi detalizēti.

Satura rādītājs

• Kas ir a2-b2 formula?
• Kvadrātu atšķirības formula
• a2 – b2 kvadrātveida formulas pierādījums
• (a + b)2 un (a – b)2 formula
• a2 – b2 Identitāte

Kas ir a ² – b ² Formula?

a ² – b ² formula algebrā ir pamatformula algebras problēmu risināšanai. To izmanto arī trigonometrisko, diferenciālo un citu problēmu risināšanai. Šī formula norāda, ka starpība starp diviem skaitļiem kvadrātā ir vienāda ar divu skaitļu summas un starpības reizinājumu, t.i.

a ² – b ² = (a + b).(a – b)

a ² – b ² Formulas definīcija

Formula a ² – b ² ļauj noteikt dispersiju starp divu skaitļu kvadrātiem bez nepieciešamības aprēķināt faktiskās kvadrātu vērtības. Izteiciens a ² – b ² formula ir šāda: a ² – b ² = (a + b).(a – b)

Kvadrātu atšķirības formula

Divu kvadrātu starpību aprēķina, izmantojot standarta algebrisko identitāti a ² – b ² . Piemēram, mums ir doti divi mainīgie, a un b, tad to kvadrātu starpība tiek aprēķināta, izmantojot formulu, a ² – b ² = (a+b).(a–b)

Būtībā kvadrātu atšķirības formula saka, ka jebkuriem diviem algebriskajiem mainīgajiem a un b izteiksme a ² – b ² ir vienāds ar mainīgo lielumu summas un starpības reizinājumu. Šo identitāti plaši izmanto, lai vienkāršotu sarežģītas algebriskas izteiksmes.

a ² – b ² Kvadrātveida formulas pierādījums

a ² – b ² identitāti var pierādīt, vienkāršojot identitātes RHS. A ² – b ² formula ir dota kā,

a ² – b ² = (a–b) (a + b)

Šī formula ir pierādīta kā

RHS = (a+b) (a–b)

⇒ RHS = a (a–b) + b (a–b)

⇒ RHS = a ² – ab + ba – b ²

⇒ RHS = a ² – ab + ab – b ²

⇒ RHS = a ² – b ²

⇒ RHS = LHS

Līdz ar to pierādīts.

a ² + b ² Formula

A ² + b ² formula ir algebriskā formula, ko izmanto, lai atrastu divu skaitļu kvadrātu summu. Kvadrātveida formulas summa tiek dota kā

a ² + b ² = (a + b) ² – 2ab

A ² + b ² formula tiek izmantota dažādu algebrisko uzdevumu risināšanai. Tālāk ir pievienotas dažādas citas svarīgas algebriskas formulas,

(a + b) ² un (a–b) ² Formula

(a + b) ² formula ir dota kā,

(a + b) ² = a ² + b ² + 2ab

(a–b) ² formula ir dota kā,

(a–b) ² = a ² + b ² – 2ab

a ² – b ² Identitāte

a ² – b ² identitāte ir viena no algebriskās identitātes ko izmanto, lai atrastu atšķirību starp divu skaitļu kvadrātiem. Šai identitātei ir dažādas lietojumprogrammas, un tā tiek dota kā

a ² – b ² = (a – b).(a + b)

Lasīt vairāk,

• Algebras formula
• Matemātikas pamatformula
• Algebriskā izteiksme

Piemēri uz a ² – b ² Formula

1. piemērs: vienkāršojiet x ² – 16

Risinājums:

= x ² – 16

= x ² - 4 ²

Mēs to zinām, a ² – b ² = (a+b) (a–b)

Ņemot vērā,

• a = x
• b = 4

= (x + 4) (x - 4)

2. piemērs: vienkāršojiet 9 g ² – 144

Risinājums:

= 9 gadi ² – 144

= (3 g.) ² – (12) ²

Mēs to zinām, a ² – b ² = (a+b)(a–b)

Ņemot vērā,

• a = 3 gadi
• b = 12

= (3 g + 12) (3 g. – 12)

3. piemērs: vienkāršošana (3x + 2) ² – (3x – 2) ²

Risinājums:

Mēs to zinām,

a ² – b ² = (a+b)(a–b)

Ņemot vērā,

• a = 3x + 2
• b = 3x – 2

(3x + 2) ² – (3x – 2) ²

= (3x + 2 + 3x - 2) (3x + 2 - (3x - 2))

= 6x (3x + 2 - 3x + 2)

= 6x(4)

= 24x

4. piemērs. Vienkāršojiet un ² – 100

Risinājums:

= un ² – 100

= un ² – (10) ²

Mēs to zinām,

a ² – b ² = (a+b)(a–b)

Ņemot vērā,

• a = un
• b = 10

= (y +10)(y –10)

5. piemērs. Novērtējiet (x + 6) (x – 6)

Risinājums:

Mēs to zinām,

(a+b) (a–b) = a ² – b ²

Ņemot vērā,

• a = x
• b = 6

(x + 6) (x - 6)

= x ² – 6 ²

= x ² – 36

6. piemērs. Novērtējiet (y + 13) (y – 13)

Risinājums:

Mēs to zinām,

(a+b) (a–b) = a ² – b ²

Ņemot vērā,

• a = un
• b = 13

(y + 13). (y - 13)

= un ² – (13) ²

= un ² – 169

7. piemērs. Novērtējiet (x + y + z). (x + y – z)

Risinājums:

Mēs to zinām,

(a+b) (a–b) = a ² – b ²

Ņemot vērā,

• a = x + y
• b = z

(x + y + z) (x + y - z)

= (x + y) ² - Ar ²

= x ² + un ² + 2xy – z ²

(a ² – b ² ) Formula – Darba lapa

Q1. Vienkāršojiet 15 ² – 14 ² izmantojot a ² – b ² identitāte.

Q2. Vienkāršojiet 11 ² – 7 ² izmantojot a ² – b ² identitāte.

Q3. Atrisiniet 23 ² – 9 ² izmantojot a ² – b ² identitāte.

Q4. Atrisiniet 9 ² – 7 ² izmantojot a ² – b ² identitāte.

a ² – b ² Formula – FAQ

1. Kas ir a ² − b ² ?

a ² – b ² formula ir formula, ko izmanto, lai atrastu atšķirību starp diviem kvadrātiem, faktiski neatrodot kvadrātu. A ² – b ² formula ir,

a ² – b ² = (a + b) (a–b)

2. Kas ir a likums ² b ² Formula?

a likums ² b ² formulas ir,

• a ² – b ² = (a + b) (a–b)
• a ² + b ² = (a + b) ² – 2ab

3. Kas ir a ² b ² Formula, ko izmanto?

a ² b ² formulas tiek izmantotas dažādu algebrisko uzdevumu risināšanai, tās tiek izmantotas arī trigonometrisko, aprēķinu un integrācijas uzdevumu vienkāršošanai.

4. Kas ir a ² b ² Formula?

Ir divi a ² b ² formulas, kas ir, a ² + b ² un a ² – b ² paplašināšanas formula a ² b ² formulas ir dotas kā

• a ² – b ² = (a + b) (a–b)
• a ² + b ² = (a + b) ² – 2ab

5. Kad ir a ² – b ² Formula tiek izmantota?

a ² – b ² formula tiek izmantota, lai atrastu atšķirību starp divu skaitļu kvadrātiem, faktiski neatrodot kvadrātus. Šo formulu izmanto arī dažādu algebrisko, trigonometrisko un citu uzdevumu risināšanai.