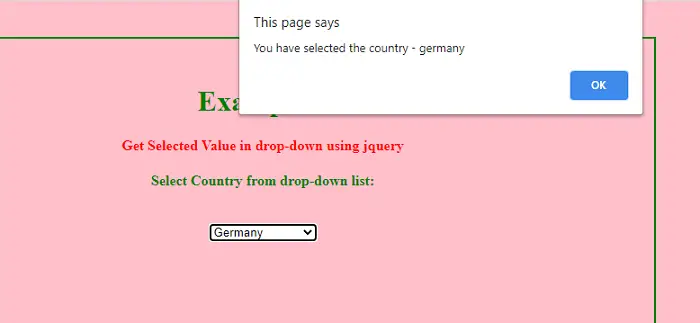
Kas yra nuo 10 iki 4 laipsnio?

Matematikoje rodikliai ir laipsniai naudojami, kai skaičius padauginamas iš savęs iš tam tikro skaičiaus kartų. Pavyzdžiui, 4 × 4 × 4= 64. Tai taip pat galima parašyti trumpąja forma kaip 4 3 = 64. Čia, 4 3 reiškia, kad skaičius 4 padauginamas iš savęs iš trijų kartų, o trumpoji – 4 3 yra eksponentinė išraiška. Skaičius 4 yra bazinis skaičius, o skaičius 3 yra eksponentas, o pateiktą eksponentinę išraišką skaitome kaip 4, pakeltą iki 3 laipsnio. Eksponentinėje išraiškoje bazė yra koeficientas, dauginamas pakartotinai iš savęs, tuo tarpu eksponentas yra koeficiento pasirodymo kartų skaičius.
Rodiklių ir galių apibrėžimas
Jei skaičius padauginamas iš savęs n kartų , gauta išraiška yra žinoma kaip n-oji galia nurodyto skaičiaus. Tarp eksponento ir galios yra labai plona skirtumo linija. Rodiklis yra skaičius, kiek kartų tam tikras skaičius buvo padaugintas iš savęs, o laipsnis yra bazinio skaičiaus sandauga, padidinta iki eksponento. Eksponentinės skaičių formos pagalba galime patogiau išreikšti itin didelius ir mažus skaičius. Pavyzdžiui, 100000000 gali būti išreikštas kaip 1 × 10 8 , o 0,0000000000013 galima išreikšti kaip 13 × 10 -13 . Tai palengvina skaičių skaitymą, padeda išlaikyti jų tikslumą ir sutaupo laiko.

Rodiklių ir galių taisyklės
Rodiklių ir laipsnių taisyklės paaiškina, kaip sudėti, atimti, dauginti ir padalyti rodiklius, taip pat kaip išspręsti įvairių rūšių matematines lygtis, apimančias eksponentus ir laipsnius.
| Produkto eksponentų įstatymas | a m × a n =a (m+ n) |
|---|---|
| Rodiklių koeficiento taisyklė | a m /a n =a (m-n) |
| Galios taisyklės galia | (a m ) n = a mn |
| Produkto taisyklės galia | a m × b m = (ab) m |
| Dalinio taisyklės galia | a m /b m = (a/b) m |
| Nulinio eksponento taisyklė | a 0 = 1 |
| Neigiamojo laipsnio taisyklė | a -m = 1/a m |
| Trupmeninių rodiklių taisyklė | a (m/n) = n √a m |
1 taisyklė: Produkto eksponentų įstatymas
Pagal šį dėsnį, kai laipsniai su tomis pačiomis bazėmis dauginami, rodikliai sumuojami.
Produkto rodiklių dėsnis: a m × a n =a (m+ n)
2 taisyklė: Rodiklių koeficiento taisyklė
Pagal šį dėsnį, norėdami padalinti du eksponentus su tomis pačiomis bazėmis, turime atimti eksponentus.
Rodiklio koeficiento taisyklė: a m /a n =a (m–n)
3 taisyklė: galios taisyklės galia
Pagal šį dėsnį, jei eksponentinis skaičius pakeliamas į kitą laipsnį, tai laipsniai dauginami.
Galios taisyklės galia: (a m ) n =a (m × n)
4 taisyklė: gaminio taisyklės galia
Pagal šį dėsnį turime padauginti skirtingas bazes ir pakelti tą patį eksponentą į bazių sandaugą.
Gaminio taisyklės galia: a m × b m =(a × b) m .
5 taisyklė: Dalinio taisyklės galia
Pagal šį dėsnį turime padalyti skirtingus pagrindus ir pakelti tą patį rodiklį į bazių koeficientą.
Dalinio taisyklės galia: a m ÷ b m =(a/b) m
6 taisyklė: Nulinio eksponento taisyklė
Pagal šį dėsnį, jei bazės, pakeltos iki nulio laipsnio, reikšmė yra 1.
Nulinio eksponento taisyklė: a 0 =1
7 taisyklė: neigiamo laipsnio taisyklė
Pagal šį dėsnį, jei rodiklis yra neigiamas, tai keičiant eksponentą į teigiamą, atsižvelgiant į eksponentinį skaičių atvirkštinę vertę.
Neigiamojo laipsnio taisyklė: a -m = 1/a m
8 taisyklė: trupmeninio rodiklio taisyklė
Pagal šį dėsnį, kai turime trupmeninį rodiklį, tada susidaro radikalai.
Trupmeninio rodiklio taisyklė: a (1/n) = n √a
a (m/n) = n √a m
Ką reiškia 10 iki 4 laipsnio?
Sprendimas:
Apskaičiuokime 10 reikšmę iki 4 vidurkio, ty 10 4
Žinome, kad pagal eksponentų galios taisyklę,
a m = a × a × a… m kartų
Taigi galime parašyti 10 4 kaip 10 × 10 × 10 × 10 = 10 000
Todėl,
10 reikšmė pakelta iki 4 laipsnio, ty 10 4 yra 10 000.
Pavyzdinės problemos
1 uždavinys: Raskite 3 reikšmę 6 .
Sprendimas:
Pateikta išraiška yra 3 6 .
Pateiktos eksponentinės išraiškos pagrindas yra 3, o eksponentas yra 6, t.
Taigi, išplėtus 3 6 , gauname 3 6 = 3 × 3 × 3 × 3 × 3 × 3 = 729
Vadinasi, 3 vertė 6 yra 729.
2 uždavinys: nustatykite (12) išraiškos eksponentą ir laipsnį 5 .
Sprendimas:
Pateikta išraiška yra 12 5 .
Pateiktos eksponentinės išraiškos pagrindas yra 12, o eksponentas yra 5, t.
3 problema: įvertinkite (2/7) -5 × (2/7) 7 .
Sprendimas:
Duota: (2/7) -5 × (2/7) 7
Mes žinome, kad a m × a n = a (m + n)
Taigi, (2/7) -5 × (2/7) 7 = (2/7) (-5+7)
= (2/7) 2 = 4/49
Taigi (2/7) -5 × (2/7) 7 = 4/49
4 uždavinys: raskite x reikšmę duotoje išraiškoje: 5 3x-2 = 625.
Sprendimas:
Atsižvelgiant į 5 3x-2 = 625.
5 3x-2 = 5 4
Palyginę panašios bazės eksponentus, gauname
⇒ 3x -2 = 4
⇒ 3x = 4 + 2 = 6
⇒ x = 6/3 = 2
Taigi x reikšmė yra 2.
5 uždavinys: raskite k reikšmę pateiktoje išraiškoje: (-2/3) 4 23) - penkiolika = (23) 7k+3
Sprendimas:
Atsižvelgiant į
(-23) 4 23) - penkiolika = (23) 7k+3
23) 4 23) - penkiolika = (23) 7k+3 {Nuo (-x) 4 = x 4 }
Mes žinome, kad a m × a n = a (m + n)
23) 4-15 = (2/3)7k+3
23) -vienuolika = (23) 7k+3
Palyginę panašios bazės eksponentus, gauname
⇒ -11 = 7k +3
⇒ 7k = -11-3 = -14
⇒ k = -14/7 = -2
Vadinasi, k reikšmė yra -2.