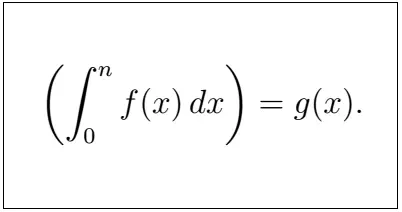Spausdinimo maksimali suma didinanti seka


Maksimalios sumos didinimo posekos problema yra rasti didžiausią tam tikros sekos sumos poseką, kad visi posekos elementai būtų surūšiuoti didėjančia tvarka.
Pavyzdžiai:
Input: [1 101 2 3 100 4 5]
Output: [1 2 3 100]
Input: [3 4 5 10]
Output: [3 4 5 10]
Input: [10 5 4 3]
Output: [10]
Input: [3 2 6 4 5 1]
Output: [3 4 5]Ankstesniame įraše aptarėme didžiausios sumos didinimo posekos problemą. Tačiau įrašas apėmė tik kodą, susijusį su didžiausios didėjančios eilės sumos radimu, bet ne su posekos konstravimu. Šiame įraše aptarsime, kaip sukurti pačią maksimalią sumą didinančią seką.
Tegul arr[0..n-1] yra įvesties masyvas. Mes apibrėžiame vektorių L taip, kad pats L[i] yra vektorius, kuriame saugoma arr[0..i] maksimali suma didėjanti seka, kuri baigiasi arr[i]. Todėl indeksui i L[i] gali būti rekursyviai parašytas kaip
L[0] = {arr[0]}
L[i] = {MaxSum(L[j])} + arr[i] where j < i and arr[j] < arr[i]
= arr[i] if there is no j such that arr[j] < arr[i]
Pavyzdžiui, masyvui [3 2 6 4 5 1]L[0]: 3
L[1]: 2
L[2]: 3 6
L[3]: 3 4
L[4]: 3 4 5
L[5]: 1C++
Žemiau yra aukščiau pateiktos idėjos įgyvendinimas -Java/* Dynamic Programming solution to construct Maximum Sum Increasing Subsequence */ #include#include using namespace std ; // Utility function to calculate sum of all // vector elements int findSum ( vector < int > arr ) { int sum = 0 ; for ( int i : arr ) sum += i ; return sum ; } // Function to construct Maximum Sum Increasing // Subsequence void printMaxSumIS ( int arr [] int n ) { // L[i] - The Maximum Sum Increasing // Subsequence that ends with arr[i] vector < vector < int > > L ( n ); // L[0] is equal to arr[0] L [ 0 ]. push_back ( arr [ 0 ]); // start from index 1 for ( int i = 1 ; i < n ; i ++ ) { // for every j less than i for ( int j = 0 ; j < i ; j ++ ) { /* L[i] = {MaxSum(L[j])} + arr[i] where j < i and arr[j] < arr[i] */ if (( arr [ i ] > arr [ j ]) && ( findSum ( L [ i ]) < findSum ( L [ j ]))) L [ i ] = L [ j ]; } // L[i] ends with arr[i] L [ i ]. push_back ( arr [ i ]); // L[i] now stores Maximum Sum Increasing // Subsequence of arr[0..i] that ends with // arr[i] } vector < int > res = L [ 0 ]; // find max for ( vector < int > x : L ) if ( findSum ( x ) > findSum ( res )) res = x ; // max will contain result for ( int i : res ) cout < < i < < ' ' ; cout < < endl ; } // Driver Code int main () { int arr [] = { 3 2 6 4 5 1 }; int n = sizeof ( arr ) / sizeof ( arr [ 0 ]); // construct and print Max Sum IS of arr printMaxSumIS ( arr n ); return 0 ; } Python/* Dynamic Programming solution to construct Maximum Sum Increasing Subsequence */ import java.util.* ; class GFG { // Utility function to calculate sum of all // vector elements static int findSum ( Vector < Integer > arr ) { int sum = 0 ; for ( int i : arr ) sum += i ; return sum ; } // Function to construct Maximum Sum Increasing // Subsequence static void printMaxSumIs ( int [] arr int n ) { // L[i] - The Maximum Sum Increasing // Subsequence that ends with arr[i] @SuppressWarnings ( 'unchecked' ) Vector < Integer >[] L = new Vector [ n ] ; for ( int i = 0 ; i < n ; i ++ ) L [ i ] = new Vector <> (); // L[0] is equal to arr[0] L [ 0 ] . add ( arr [ 0 ] ); // start from index 1 for ( int i = 1 ; i < n ; i ++ ) { // for every j less than i for ( int j = 0 ; j < i ; j ++ ) { /* * L[i] = {MaxSum(L[j])} + arr[i] where j < i and arr[j] < arr[i] */ if (( arr [ i ] > arr [ j ] ) && ( findSum ( L [ i ] ) < findSum ( L [ j ] ))) { for ( int k : L [ j ] ) if ( ! L [ i ] . contains ( k )) L [ i ] . add ( k ); } } // L[i] ends with arr[i] L [ i ] . add ( arr [ i ] ); // L[i] now stores Maximum Sum Increasing // Subsequence of arr[0..i] that ends with // arr[i] } Vector < Integer > res = new Vector <> ( L [ 0 ] ); // res = L[0]; // find max for ( Vector < Integer > x : L ) if ( findSum ( x ) > findSum ( res )) res = x ; // max will contain result for ( int i : res ) System . out . print ( i + ' ' ); System . out . println (); } // Driver Code public static void main ( String [] args ) { int [] arr = { 3 2 6 4 5 1 }; int n = arr . length ; // construct and print Max Sum IS of arr printMaxSumIs ( arr n ); } } // This code is contributed by // sanjeev2552C## Dynamic Programming solution to construct # Maximum Sum Increasing Subsequence */ # Utility function to calculate sum of all # vector elements def findSum ( arr ): summ = 0 for i in arr : summ += i return summ # Function to construct Maximum Sum Increasing # Subsequence def printMaxSumIS ( arr n ): # L[i] - The Maximum Sum Increasing # Subsequence that ends with arr[i] L = [[] for i in range ( n )] # L[0] is equal to arr[0] L [ 0 ] . append ( arr [ 0 ]) # start from index 1 for i in range ( 1 n ): # for every j less than i for j in range ( i ): # L[i] = {MaxSum(L[j])} + arr[i] # where j < i and arr[j] < arr[i] if (( arr [ i ] > arr [ j ]) and ( findSum ( L [ i ]) < findSum ( L [ j ]))): for e in L [ j ]: if e not in L [ i ]: L [ i ] . append ( e ) # L[i] ends with arr[i] L [ i ] . append ( arr [ i ]) # L[i] now stores Maximum Sum Increasing # Subsequence of arr[0..i] that ends with # arr[i] res = L [ 0 ] # find max for x in L : if ( findSum ( x ) > findSum ( res )): res = x # max will contain result for i in res : print ( i end = ' ' ) # Driver Code arr = [ 3 2 6 4 5 1 ] n = len ( arr ) # construct and prMax Sum IS of arr printMaxSumIS ( arr n ) # This code is contributed by Mohit KumarJavaScript/* Dynamic Programming solution to construct Maximum Sum Increasing Subsequence */ using System ; using System.Collections.Generic ; class GFG { // Utility function to calculate sum of all // vector elements static int findSum ( List < int > arr ) { int sum = 0 ; foreach ( int i in arr ) sum += i ; return sum ; } // Function to construct Maximum Sum Increasing // Subsequence static void printMaxSumIs ( int [] arr int n ) { // L[i] - The Maximum Sum Increasing // Subsequence that ends with arr[i] List < int > [] L = new List < int > [ n ]; for ( int i = 0 ; i < n ; i ++ ) L [ i ] = new List < int > (); // L[0] is equal to arr[0] L [ 0 ]. Add ( arr [ 0 ]); // start from index 1 for ( int i = 1 ; i < n ; i ++ ) { // for every j less than i for ( int j = 0 ; j < i ; j ++ ) { /* * L[i] = {MaxSum(L[j])} + arr[i] where j < i and arr[j] < arr[i] */ if (( arr [ i ] > arr [ j ]) && ( findSum ( L [ i ]) < findSum ( L [ j ]))) { foreach ( int k in L [ j ]) if ( ! L [ i ]. Contains ( k )) L [ i ] . Add ( k ); } } // L[i] ends with arr[i] L [ i ]. Add ( arr [ i ]); // L[i] now stores Maximum Sum Increasing // Subsequence of arr[0..i] that ends with // arr[i] } List < int > res = new List < int > ( L [ 0 ]); // res = L[0]; // find max foreach ( List < int > x in L ) if ( findSum ( x ) > findSum ( res )) res = x ; // max will contain result foreach ( int i in res ) Console . Write ( i + ' ' ); Console . WriteLine (); } // Driver Code public static void Main ( String [] args ) { int [] arr = { 3 2 6 4 5 1 }; int n = arr . Length ; // construct and print Max Sum IS of arr printMaxSumIs ( arr n ); } } // This code is contributed by PrinciRaj1992
' ); } // Driver Code let arr = [ 3 2 6 4 5 1 ]; let n = arr . length ; // construct and print Max Sum IS of arr printMaxSumIs ( arr n ); // This code is contributed by unknown2108 < /script>
Išvestis3 4 5
Aukščiau pateiktą DP sprendimą galime optimizuoti pašalindami funkciją findSum (). Vietoj to galime išlaikyti kitą vektorių / masyvą, kad išsaugotume didžiausios sumos didėjančios posekos sumą, kuri baigiasi arr[i].Laiko sudėtingumas dinaminio programavimo sprendimas yra O(n 2 ).
Pagalbinė erdvė programos naudojamas O (n 2 ).2 metodas: ( Naudojant Dinaminis programavimas naudojant O(N) erdvę
Aukščiau pateiktas metodas apėmė, kaip sukurti didžiausią sumą didinančią seką O(N 2 ) laikas ir O(N 2 ) erdvė. Taikydami šį metodą optimizuosime erdvės sudėtingumą ir sukursime maksimalią sumą didinančią seką O(N) 2 ) laikas ir O(N) erdvė.
- Tegul arr[0..n-1] yra įvesties masyvas.
- Mes apibrėžiame porų L vektorių taip, kad L[i] pirmiausia išsaugotų arr[0..i] didžiausios sumos didinimo seką, kuri baigiasi arr[i], o L[i].second saugo ankstesnio elemento, naudoto sumai generuoti, indeksą.
- Kadangi pirmasis elementas neturi ankstesnio elemento, jo indeksas L[0] būtų -1.
Pavyzdžiui
array = [3 2 6 4 5 1]
L[0]: {3 -1}
L[1]: {2 1}
L[2]: {9 0}
L[3]: {7 0}
L[4]: {12 3}
L[5]: {1 5}Kaip matome aukščiau, maksimalios sumos didinimo posekos reikšmė yra 12. Norėdami sukurti tikrąją poseką, naudosime indeksą, saugomą L[i].second. Toliau pateikiami posekos kūrimo žingsniai:
- Vektoriniame rezultate išsaugokite elemento, kuriame buvo rasta didžiausios sumos didinimo posekos, reikšmę (ty currIndex = 4). Taigi į rezultato vektorių įtrauksime arr[currIndex].
- Atnaujinkite currIndex į L[currIndex].second ir kartokite 1 veiksmą, kol currIndex nebus -1 arba nepasikeis (ty currIndex == previousIndex).
- Rodyti rezultatų vektoriaus elementus atvirkštine tvarka.
Žemiau pateikiamas aukščiau pateiktos idėjos įgyvendinimas:
C++14 /* Dynamic Programming solution to construct Maximum Sum Increasing Subsequence */ #include using namespace std ; // Function to construct and print the Maximum Sum // Increasing Subsequence void constructMaxSumIS ( vector < int > arr int n ) { // L[i] stores the value of Maximum Sum Increasing // Subsequence that ends with arr[i] and the index of // previous element used to construct the Subsequence vector < pair < int int > > L ( n ); int index = 0 ; for ( int i : arr ) { L [ index ] = { i index }; index ++ ; } // Set L[0].second equal to -1 L [ 0 ]. second = -1 ; // start from index 1 for ( int i = 1 ; i < n ; i ++ ) { // for every j less than i for ( int j = 0 ; j < i ; j ++ ) { if ( arr [ i ] > arr [ j ] and L [ i ]. first < arr [ i ] + L [ j ]. first ) { L [ i ]. first = arr [ i ] + L [ j ]. first ; L [ i ]. second = j ; } } } int maxi = INT_MIN currIndex track = 0 ; for ( auto p : L ) { if ( p . first > maxi ) { maxi = p . first ; currIndex = track ; } track ++ ; } // Stores the final Subsequence vector < int > result ; // Index of previous element // used to construct the Subsequence int prevoiusIndex ; while ( currIndex >= 0 ) { result . push_back ( arr [ currIndex ]); prevoiusIndex = L [ currIndex ]. second ; if ( currIndex == prevoiusIndex ) break ; currIndex = prevoiusIndex ; } for ( int i = result . size () - 1 ; i >= 0 ; i -- ) cout < < result [ i ] < < ' ' ; } // Driver Code int main () { vector < int > arr = { 1 101 2 3 100 4 5 }; int n = arr . size (); // Function call constructMaxSumIS ( arr n ); return 0 ; }
Java // Dynamic Programming solution to construct // Maximum Sum Increasing Subsequence import java.util.* ; import java.awt.Point ; class GFG { // Function to construct and print the Maximum Sum // Increasing Subsequence static void constructMaxSumIS ( List < Integer > arr int n ) { // L.get(i) stores the value of Maximum Sum Increasing // Subsequence that ends with arr.get(i) and the index of // previous element used to construct the Subsequence List < Point > L = new ArrayList < Point > (); int index = 0 ; for ( int i : arr ) { L . add ( new Point ( i index )); index ++ ; } // Set L[0].second equal to -1 L . set ( 0 new Point ( L . get ( 0 ). x - 1 )); // Start from index 1 for ( int i = 1 ; i < n ; i ++ ) { // For every j less than i for ( int j = 0 ; j < i ; j ++ ) { if ( arr . get ( i ) > arr . get ( j ) && L . get ( i ). x < arr . get ( i ) + L . get ( j ). x ) { L . set ( i new Point ( arr . get ( i ) + L . get ( j ). x j )); } } } int maxi = - 100000000 currIndex = 0 track = 0 ; for ( Point p : L ) { if ( p . x > maxi ) { maxi = p . x ; currIndex = track ; } track ++ ; } // Stores the final Subsequence List < Integer > result = new ArrayList < Integer > (); // Index of previous element // used to construct the Subsequence int prevoiusIndex ; while ( currIndex >= 0 ) { result . add ( arr . get ( currIndex )); prevoiusIndex = L . get ( currIndex ). y ; if ( currIndex == prevoiusIndex ) break ; currIndex = prevoiusIndex ; } for ( int i = result . size () - 1 ; i >= 0 ; i -- ) System . out . print ( result . get ( i ) + ' ' ); } // Driver Code public static void main ( String [] s ) { List < Integer > arr = new ArrayList < Integer > (); arr . add ( 1 ); arr . add ( 101 ); arr . add ( 2 ); arr . add ( 3 ); arr . add ( 100 ); arr . add ( 4 ); arr . add ( 5 ); int n = arr . size (); // Function call constructMaxSumIS ( arr n ); } } // This code is contributed by rutvik_56
Python # Dynamic Programming solution to construct # Maximum Sum Increasing Subsequence import sys # Function to construct and print the Maximum Sum # Increasing Subsequence def constructMaxSumIS ( arr n ) : # L[i] stores the value of Maximum Sum Increasing # Subsequence that ends with arr[i] and the index of # previous element used to construct the Subsequence L = [] index = 0 for i in arr : L . append ([ i index ]) index += 1 # Set L[0].second equal to -1 L [ 0 ][ 1 ] = - 1 # start from index 1 for i in range ( 1 n ) : # for every j less than i for j in range ( i ) : if ( arr [ i ] > arr [ j ] and L [ i ][ 0 ] < arr [ i ] + L [ j ][ 0 ]) : L [ i ][ 0 ] = arr [ i ] + L [ j ][ 0 ] L [ i ][ 1 ] = j maxi currIndex track = - sys . maxsize 0 0 for p in L : if ( p [ 0 ] > maxi ) : maxi = p [ 0 ] currIndex = track track += 1 # Stores the final Subsequence result = [] while ( currIndex >= 0 ) : result . append ( arr [ currIndex ]) prevoiusIndex = L [ currIndex ][ 1 ] if ( currIndex == prevoiusIndex ) : break currIndex = prevoiusIndex for i in range ( len ( result ) - 1 - 1 - 1 ) : print ( result [ i ] end = ' ' ) arr = [ 1 101 2 3 100 4 5 ] n = len ( arr ) # Function call constructMaxSumIS ( arr n ) # This code is contributed by divyeshrabadiya07
C# /* Dynamic Programming solution to construct Maximum Sum Increasing Subsequence */ using System ; using System.Collections.Generic ; class GFG { // Function to construct and print the Maximum Sum // Increasing Subsequence static void constructMaxSumIS ( List < int > arr int n ) { // L[i] stores the value of Maximum Sum Increasing // Subsequence that ends with arr[i] and the index of // previous element used to construct the Subsequence List < Tuple < int int >> L = new List < Tuple < int int >> (); int index = 0 ; foreach ( int i in arr ) { L . Add ( new Tuple < int int > ( i index )); index ++ ; } // Set L[0].second equal to -1 L [ 0 ] = new Tuple < int int > ( L [ 0 ]. Item1 - 1 ); // start from index 1 for ( int i = 1 ; i < n ; i ++ ) { // for every j less than i for ( int j = 0 ; j < i ; j ++ ) { if ( arr [ i ] > arr [ j ] && L [ i ]. Item1 < arr [ i ] + L [ j ]. Item1 ) { L [ i ] = new Tuple < int int > ( arr [ i ] + L [ j ]. Item1 j ); } } } int maxi = Int32 . MinValue currIndex = 0 track = 0 ; foreach ( Tuple < int int > p in L ) { if ( p . Item1 > maxi ) { maxi = p . Item1 ; currIndex = track ; } track ++ ; } // Stores the final Subsequence List < int > result = new List < int > (); // Index of previous element // used to construct the Subsequence int prevoiusIndex ; while ( currIndex >= 0 ) { result . Add ( arr [ currIndex ]); prevoiusIndex = L [ currIndex ]. Item2 ; if ( currIndex == prevoiusIndex ) break ; currIndex = prevoiusIndex ; } for ( int i = result . Count - 1 ; i >= 0 ; i -- ) Console . Write ( result [ i ] + ' ' ); } static void Main () { List < int > arr = new List < int > ( new int [] { 1 101 2 3 100 4 5 }); int n = arr . Count ; // Function call constructMaxSumIS ( arr n ); } } // This code is contributed by divyesh072019
JavaScript < script > // Dynamic Programming solution to construct // Maximum Sum Increasing Subsequence // Function to construct and print the Maximum Sum // Increasing Subsequence function constructMaxSumIS ( arr n ){ // L[i] stores the value of Maximum Sum Increasing // Subsequence that ends with arr[i] and the index of // previous element used to construct the Subsequence let L = [] let index = 0 for ( let i of arr ){ L . push ([ i index ]) index += 1 } // Set L[0].second equal to -1 L [ 0 ][ 1 ] = - 1 // start from index 1 for ( let i = 1 ; i < n ; i ++ ){ // for every j less than i for ( let j = 0 ; j < i ; j ++ ){ if ( arr [ i ] > arr [ j ] && L [ i ][ 0 ] < arr [ i ] + L [ j ][ 0 ]){ L [ i ][ 0 ] = arr [ i ] + L [ j ][ 0 ] L [ i ][ 1 ] = j } } } let maxi = Number . MIN_VALUE currIndex = 0 track = 0 for ( let p of L ){ if ( p [ 0 ] > maxi ){ maxi = p [ 0 ] currIndex = track } track += 1 } // Stores the final Subsequence let result = [] while ( currIndex >= 0 ){ result . push ( arr [ currIndex ]) let prevoiusIndex = L [ currIndex ][ 1 ] if ( currIndex == prevoiusIndex ) break currIndex = prevoiusIndex } for ( let i = result . length - 1 ; i >= 0 ; i -- ) document . write ( result [ i ] ' ' ) } let arr = [ 1 101 2 3 100 4 5 ] let n = arr . length // Function call constructMaxSumIS ( arr n ) // This code is contributed by shinjanpatra < /script>
Išvestis
1 2 3 100
Laiko sudėtingumas: O (N 2 )
Erdvės sudėtingumas: O(N)