n-arinio medžio LCA | Nuolatinė užklausa O(1)
Mes matėme įvairius metodus su skirtingu laiko sudėtingumu, kaip apskaičiuoti LCA n-ariame medyje:
1 būdas: Naivus metodas (skaičiuojant kelią nuo šaknies iki mazgo) | O(n) vienai užklausai
2 būdas: Naudojant Sqrt Decomposition | O (sqrt H)
3 būdas: Naudojant Sparse Matrix DP metodą | O (prisijungti)
Išstudijuokime kitą metodą, kurio užklausos laikas yra greitesnis nei visi pirmiau minėti metodai. Taigi mūsų tikslas bus apskaičiuoti LCA pastovus laikas ~ O(1) . Pažiūrėkime, kaip galime tai pasiekti.
4 būdas: Minimalios diapazono užklausos naudojimas
Mes aptarėme LCA ir RMQ dvejetainiam medžiui . Čia aptariame LCA problemą į RMQ problemos konvertavimą n-ariniam medžiui.
Pre-requisites:- LCA in Binary Tree using RMQ RMQ using sparse table
Pagrindinė koncepcija: Taikydami šį metodą, sumažinsime savo LCA problemą iki RMQ (minimalios užklausos diapazono) problemos per statinį masyvą. Kai tai padarysime, minimalaus diapazono užklausas susiesime su reikiamomis LCA užklausomis.
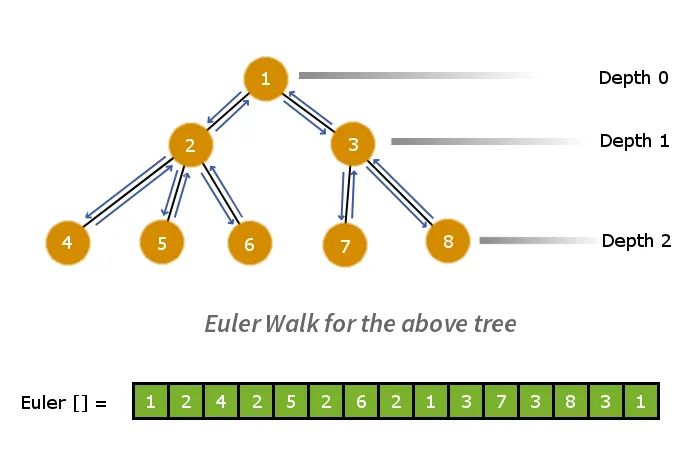
Pirmasis žingsnis bus išskaidyti medį į plokščią linijinį masyvą. Norėdami tai padaryti, galime pritaikyti Eulerio eiseną. Eulerio ėjimas leis iš anksto užsakyti grafiką. Taigi atliksime Eulerio ėjimą ant medžio ir išsaugosime mazgus masyve, kai juos aplankysime. Šis procesas sumažina medį > 
Dabar pamąstykime bendrai: apsvarstykite bet kuriuos du medžio mazgus. Bus tiksliai vienas kelias, jungiantis abu mazgus, o mazgas, kurio gylio reikšmė kelyje yra mažiausia, bus dviejų nurodytų mazgų LCA.
Dabar paimkite bet kuriuos du skirtingus mazgus in ir v Eulerio eisenos masyve. Dabar visi elementai kelyje nuo u iki v bus tarp mazgų u ir v indekso Eulerio eigos masyve. Todėl mums tereikia apskaičiuoti mazgą, kurio gylis tarp mazgo u ir mazgo v indekso yra minimalus eulerio masyve.
Tam palaikysime kitą masyvą, kuriame bus visų mazgų gylis, atitinkantis jų padėtį Eulerio eigos masyve, kad galėtume jame pritaikyti savo RMQ algoritmą.
Žemiau pateikta Eulerio eigos matrica, lygiagreti jos gylio takelių masyvai.

Pavyzdys: Apsvarstykite du mazgus mazgas 6 ir mazgas 7 eulerio masyve. Norėdami apskaičiuoti 6 ir 7 mazgų LCA, žiūrime į mažiausią gylio reikšmę visiems mazgams tarp 6 ir 7 mazgų.
Todėl mazgas 1 turi mažiausią gylio vertė = 0 taigi tai yra 6 ir 7 mazgų LCA.

Įgyvendinimas: -
We will be maintaining three arrays 1) Euler Path 2) Depth array 3) First Appearance Index
Eulerio kelias ir gylio masyvas yra tokie patys, kaip aprašyta aukščiau
Pirmojo pasirodymo indeksas FAI[]: Pirmosios išvaizdos indekso masyve bus saugomas kiekvieno Eulerio kelio masyvo mazgo pirmosios pozicijos indeksas. FAI[i] = Pirmasis i-ojo mazgo pasirodymas Euler Walk masyve.
Aukščiau pateikto metodo įgyvendinimas pateiktas žemiau:
Įgyvendinimas:
C++ // C++ program to demonstrate LCA of n-ary tree // in constant time. #include 'bits/stdc++.h' using namespace std ; #define sz 101 vector < int > adj [ sz ]; // stores the tree vector < int > euler ; // tracks the eulerwalk vector < int > depthArr ; // depth for each node corresponding // to eulerwalk int FAI [ sz ]; // stores first appearance index of every node int level [ sz ]; // stores depth for all nodes in the tree int ptr ; // pointer to euler walk int dp [ sz ][ 18 ]; // sparse table int logn [ sz ]; // stores log values int p2 [ 20 ]; // stores power of 2 void buildSparseTable ( int n ) { // initializing sparse table memset ( dp -1 sizeof ( dp )); // filling base case values for ( int i = 1 ; i < n ; i ++ ) dp [ i -1 ][ 0 ] = ( depthArr [ i ] > depthArr [ i -1 ]) ? i -1 : i ; // dp to fill sparse table for ( int l = 1 ; l < 15 ; l ++ ) for ( int i = 0 ; i < n ; i ++ ) if ( dp [ i ][ l -1 ] != -1 and dp [ i + p2 [ l -1 ]][ l -1 ] != -1 ) dp [ i ][ l ] = ( depthArr [ dp [ i ][ l -1 ]] > depthArr [ dp [ i + p2 [ l -1 ]][ l -1 ]]) ? dp [ i + p2 [ l -1 ]][ l -1 ] : dp [ i ][ l -1 ]; else break ; } int query ( int l int r ) { int d = r - l ; int dx = logn [ d ]; if ( l == r ) return l ; if ( depthArr [ dp [ l ][ dx ]] > depthArr [ dp [ r - p2 [ dx ]][ dx ]]) return dp [ r - p2 [ dx ]][ dx ]; else return dp [ l ][ dx ]; } void preprocess () { // memorizing powers of 2 p2 [ 0 ] = 1 ; for ( int i = 1 ; i < 18 ; i ++ ) p2 [ i ] = p2 [ i -1 ] * 2 ; // memorizing all log(n) values int val = 1 ptr = 0 ; for ( int i = 1 ; i < sz ; i ++ ) { logn [ i ] = ptr -1 ; if ( val == i ) { val *= 2 ; logn [ i ] = ptr ; ptr ++ ; } } } /** * Euler Walk ( preorder traversal) * converting tree to linear depthArray * Time Complexity : O(n) * */ void dfs ( int cur int prev int dep ) { // marking FAI for cur node if ( FAI [ cur ] == -1 ) FAI [ cur ] = ptr ; level [ cur ] = dep ; // pushing root to euler walk euler . push_back ( cur ); // incrementing euler walk pointer ptr ++ ; for ( auto x : adj [ cur ]) { if ( x != prev ) { dfs ( x cur dep + 1 ); // pushing cur again in backtrack // of euler walk euler . push_back ( cur ); // increment euler walk pointer ptr ++ ; } } } // Create Level depthArray corresponding // to the Euler walk Array void makeArr () { for ( auto x : euler ) depthArr . push_back ( level [ x ]); } int LCA ( int u int v ) { // trivial case if ( u == v ) return u ; if ( FAI [ u ] > FAI [ v ]) swap ( u v ); // doing RMQ in the required range return euler [ query ( FAI [ u ] FAI [ v ])]; } void addEdge ( int u int v ) { adj [ u ]. push_back ( v ); adj [ v ]. push_back ( u ); } int main ( int argc char const * argv []) { // constructing the described tree int numberOfNodes = 8 ; addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 2 4 ); addEdge ( 2 5 ); addEdge ( 2 6 ); addEdge ( 3 7 ); addEdge ( 3 8 ); // performing required precalculations preprocess (); // doing the Euler walk ptr = 0 ; memset ( FAI -1 sizeof ( FAI )); dfs ( 1 0 0 ); // creating depthArray corresponding to euler[] makeArr (); // building sparse table buildSparseTable ( depthArr . size ()); cout < < 'LCA(67) : ' < < LCA ( 6 7 ) < < ' n ' ; cout < < 'LCA(64) : ' < < LCA ( 6 4 ) < < ' n ' ; return 0 ; }
Java // Java program to demonstrate LCA of n-ary // tree in constant time. import java.util.ArrayList ; import java.util.Arrays ; class GFG { static int sz = 101 ; @SuppressWarnings ( 'unchecked' ) // Stores the tree static ArrayList < Integer >[] adj = new ArrayList [ sz ] ; // Tracks the eulerwalk static ArrayList < Integer > euler = new ArrayList <> (); // Depth for each node corresponding static ArrayList < Integer > depthArr = new ArrayList <> (); // to eulerwalk // Stores first appearance index of every node static int [] FAI = new int [ sz ] ; // Stores depth for all nodes in the tree static int [] level = new int [ sz ] ; // Pointer to euler walk static int ptr ; // Sparse table static int [][] dp = new int [ sz ][ 18 ] ; // Stores log values static int [] logn = new int [ sz ] ; // Stores power of 2 static int [] p2 = new int [ 20 ] ; static void buildSparseTable ( int n ) { // Initializing sparse table for ( int i = 0 ; i < sz ; i ++ ) { for ( int j = 0 ; j < 18 ; j ++ ) { dp [ i ][ j ] = - 1 ; } } // Filling base case values for ( int i = 1 ; i < n ; i ++ ) dp [ i - 1 ][ 0 ] = ( depthArr . get ( i ) > depthArr . get ( i - 1 )) ? i - 1 : i ; // dp to fill sparse table for ( int l = 1 ; l < 15 ; l ++ ) for ( int i = 0 ; i < n ; i ++ ) if ( dp [ i ][ l - 1 ] != - 1 && dp [ i + p2 [ l - 1 ]][ l - 1 ] != - 1 ) dp [ i ][ l ] = ( depthArr . get ( dp [ i ][ l - 1 ] ) > depthArr . get ( dp [ i + p2 [ l - 1 ]][ l - 1 ] )) ? dp [ i + p2 [ l - 1 ]][ l - 1 ] : dp [ i ][ l - 1 ] ; else break ; } static int query ( int l int r ) { int d = r - l ; int dx = logn [ d ] ; if ( l == r ) return l ; if ( depthArr . get ( dp [ l ][ dx ] ) > depthArr . get ( dp [ r - p2 [ dx ]][ dx ] )) return dp [ r - p2 [ dx ]][ dx ] ; else return dp [ l ][ dx ] ; } static void preprocess () { // Memorizing powers of 2 p2 [ 0 ] = 1 ; for ( int i = 1 ; i < 18 ; i ++ ) p2 [ i ] = p2 [ i - 1 ] * 2 ; // Memorizing all log(n) values int val = 1 ptr = 0 ; for ( int i = 1 ; i < sz ; i ++ ) { logn [ i ] = ptr - 1 ; if ( val == i ) { val *= 2 ; logn [ i ] = ptr ; ptr ++ ; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs ( int cur int prev int dep ) { // Marking FAI for cur node if ( FAI [ cur ] == - 1 ) FAI [ cur ] = ptr ; level [ cur ] = dep ; // Pushing root to euler walk euler . add ( cur ); // Incrementing euler walk pointer ptr ++ ; for ( Integer x : adj [ cur ] ) { if ( x != prev ) { dfs ( x cur dep + 1 ); // Pushing cur again in backtrack // of euler walk euler . add ( cur ); // Increment euler walk pointer ptr ++ ; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr () { for ( Integer x : euler ) depthArr . add ( level [ x ] ); } static int LCA ( int u int v ) { // Trivial case if ( u == v ) return u ; if ( FAI [ u ] > FAI [ v ] ) { int temp = u ; u = v ; v = temp ; } // Doing RMQ in the required range return euler . get ( query ( FAI [ u ] FAI [ v ] )); } static void addEdge ( int u int v ) { adj [ u ] . add ( v ); adj [ v ] . add ( u ); } // Driver code public static void main ( String [] args ) { for ( int i = 0 ; i < sz ; i ++ ) { adj [ i ] = new ArrayList <> (); } // Constructing the described tree int numberOfNodes = 8 ; addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 2 4 ); addEdge ( 2 5 ); addEdge ( 2 6 ); addEdge ( 3 7 ); addEdge ( 3 8 ); // Performing required precalculations preprocess (); // Doing the Euler walk ptr = 0 ; Arrays . fill ( FAI - 1 ); dfs ( 1 0 0 ); // Creating depthArray corresponding to euler[] makeArr (); // Building sparse table buildSparseTable ( depthArr . size ()); System . out . println ( 'LCA(67) : ' + LCA ( 6 7 )); System . out . println ( 'LCA(64) : ' + LCA ( 6 4 )); } } // This code is contributed by sanjeev2552
Python3 # Python program to demonstrate LCA of n-ary tree # in constant time. from typing import List # stores the tree adj = [[] for _ in range ( 101 )] # tracks the eulerwalk euler = [] # depth for each node corresponding to eulerwalk depthArr = [] # stores first appearance index of every node FAI = [ - 1 ] * 101 # stores depth for all nodes in the tree level = [ 0 ] * 101 # pointer to euler walk ptr = 0 # sparse table dp = [[ - 1 ] * 18 for _ in range ( 101 )] # stores log values logn = [ 0 ] * 101 # stores power of 2 p2 = [ 0 ] * 20 def buildSparseTable ( n : int ): # initializing sparse table for i in range ( n ): dp [ i ][ 0 ] = i - 1 if depthArr [ i ] > depthArr [ i - 1 ] else i # dp to fill sparse table for l in range ( 1 15 ): for i in range ( n ): if dp [ i ][ l - 1 ] != - 1 and dp [ i + p2 [ l - 1 ]][ l - 1 ] != - 1 : dp [ i ][ l ] = dp [ i + p2 [ l - 1 ]][ l - 1 ] if depthArr [ dp [ i ][ l - 1 ] ] > depthArr [ dp [ i + p2 [ l - 1 ]][ l - 1 ]] else dp [ i ][ l - 1 ] else : break def query ( l : int r : int ) -> int : d = r - l dx = logn [ d ] if l == r : return l if depthArr [ dp [ l ][ dx ]] > depthArr [ dp [ r - p2 [ dx ]][ dx ]]: return dp [ r - p2 [ dx ]][ dx ] else : return dp [ l ][ dx ] def preprocess (): global ptr # memorizing powers of 2 p2 [ 0 ] = 1 for i in range ( 1 18 ): p2 [ i ] = p2 [ i - 1 ] * 2 # memorizing all log(n) values val = 1 ptr = 0 for i in range ( 1 101 ): logn [ i ] = ptr - 1 if val == i : val *= 2 logn [ i ] = ptr ptr += 1 def dfs ( cur : int prev : int dep : int ): global ptr # marking FAI for cur node if FAI [ cur ] == - 1 : FAI [ cur ] = ptr level [ cur ] = dep # pushing root to euler walk euler . append ( cur ) # incrementing euler walk pointer ptr += 1 for x in adj [ cur ]: if x != prev : dfs ( x cur dep + 1 ) # pushing cur again in backtrack # of euler walk euler . append ( cur ) # increment euler walk pointer ptr += 1 # Create Level depthArray corresponding # to the Euler walk Array def makeArr (): global depthArr for x in euler : depthArr . append ( level [ x ]) def LCA ( u : int v : int ) -> int : # trivial case if u == v : return u if FAI [ u ] > FAI [ v ]: u v = v u # doing RMQ in the required range return euler [ query ( FAI [ u ] FAI [ v ])] def addEdge ( u v ): adj [ u ] . append ( v ) adj [ v ] . append ( u ) # constructing the described tree numberOfNodes = 8 addEdge ( 1 2 ) addEdge ( 1 3 ) addEdge ( 2 4 ) addEdge ( 2 5 ) addEdge ( 2 6 ) addEdge ( 3 7 ) addEdge ( 3 8 ) # performing required precalculations preprocess () # doing the Euler walk ptr = 0 FAI = [ - 1 ] * ( numberOfNodes + 1 ) dfs ( 1 0 0 ) # creating depthArray corresponding to euler[] makeArr () # building sparse table buildSparseTable ( len ( depthArr )) print ( 'LCA(67) : ' LCA ( 6 7 )) print ( 'LCA(64) : ' LCA ( 6 4 ))
C# // C# program to demonstrate LCA of n-ary // tree in constant time. using System ; using System.Collections.Generic ; public class GFG { static int sz = 101 ; // Stores the tree static List < int > [] adj = new List < int > [ sz ]; // Tracks the eulerwalk static List < int > euler = new List < int > (); // Depth for each node corresponding static List < int > depthArr = new List < int > (); // to eulerwalk // Stores first appearance index of every node static int [] FAI = new int [ sz ]; // Stores depth for all nodes in the tree static int [] level = new int [ sz ]; // Pointer to euler walk static int ptr ; // Sparse table static int [] dp = new int [ sz 18 ]; // Stores log values static int [] logn = new int [ sz ]; // Stores power of 2 static int [] p2 = new int [ 20 ]; static void buildSparseTable ( int n ) { // Initializing sparse table for ( int i = 0 ; i < sz ; i ++ ) { for ( int j = 0 ; j < 18 ; j ++ ) { dp [ i j ] = - 1 ; } } // Filling base case values for ( int i = 1 ; i < n ; i ++ ) dp [ i - 1 0 ] = ( depthArr [ i ] > depthArr [ i - 1 ]) ? i - 1 : i ; // dp to fill sparse table for ( int l = 1 ; l < 15 ; l ++ ) for ( int i = 0 ; i < n ; i ++ ) if ( dp [ i l - 1 ] != - 1 && dp [ i + p2 [ l - 1 ] l - 1 ] != - 1 ) dp [ i l ] = ( depthArr [ dp [ i l - 1 ]] > depthArr [ dp [ i + p2 [ l - 1 ] l - 1 ]]) ? dp [ i + p2 [ l - 1 ] l - 1 ] : dp [ i l - 1 ]; else break ; } static int query ( int l int r ) { int d = r - l ; int dx = logn [ d ]; if ( l == r ) return l ; if ( depthArr [ dp [ l dx ]] > depthArr [ dp [ r - p2 [ dx ] dx ]]) return dp [ r - p2 [ dx ] dx ]; else return dp [ l dx ]; } static void preprocess () { // Memorizing powers of 2 p2 [ 0 ] = 1 ; for ( int i = 1 ; i < 18 ; i ++ ) p2 [ i ] = p2 [ i - 1 ] * 2 ; // Memorizing all log(n) values int val = 1 ptr = 0 ; for ( int i = 1 ; i < sz ; i ++ ) { logn [ i ] = ptr - 1 ; if ( val == i ) { val *= 2 ; logn [ i ] = ptr ; ptr ++ ; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs ( int cur int prev int dep ) { // Marking FAI for cur node if ( FAI [ cur ] == - 1 ) FAI [ cur ] = ptr ; level [ cur ] = dep ; // Pushing root to euler walk euler . Add ( cur ); // Incrementing euler walk pointer ptr ++ ; foreach ( int x in adj [ cur ]) { if ( x != prev ) { dfs ( x cur dep + 1 ); euler . Add ( cur ); ptr ++ ; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr () { foreach ( int x in euler ) depthArr . Add ( level [ x ]); } static int LCA ( int u int v ) { // Trivial case if ( u == v ) return u ; if ( FAI [ u ] > FAI [ v ]) { int temp = u ; u = v ; v = temp ; } // Doing RMQ in the required range return euler [ query ( FAI [ u ] FAI [ v ])]; } static void addEdge ( int u int v ) { adj [ u ]. Add ( v ); adj [ v ]. Add ( u ); } // Driver Code static void Main ( string [] args ) { int sz = 9 ; adj = new List < int > [ sz ]; for ( int i = 0 ; i < sz ; i ++ ) { adj [ i ] = new List < int > (); } // Constructing the described tree int numberOfNodes = 8 ; addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 2 4 ); addEdge ( 2 5 ); addEdge ( 2 6 ); addEdge ( 3 7 ); addEdge ( 3 8 ); // Performing required precalculations preprocess (); // Doing the Euler walk ptr = 0 ; Array . Fill ( FAI - 1 ); dfs ( 1 0 0 ); // Creating depthArray corresponding to euler[] makeArr (); // Building sparse table buildSparseTable ( depthArr . Count ); Console . WriteLine ( 'LCA(67) : ' + LCA ( 6 7 )); Console . WriteLine ( 'LCA(64) : ' + LCA ( 6 4 )); } } // This code is contributed by Prince Kumar
JavaScript let adj = []; for ( let _ = 0 ; _ < 101 ; _ ++ ) { adj . push ([]); } // tracks the eulerwalk let euler = []; // depth for each node corresponding to eulerwalk let depthArr = []; // stores first appearance index of every node let FAI = new Array ( 101 ). fill ( - 1 ); // stores depth for all nodes in the tree let level = new Array ( 101 ). fill ( 0 ); // pointer to euler walk let ptr = 0 ; // sparse table let dp = []; for ( let _ = 0 ; _ < 101 ; _ ++ ) { dp . push ( new Array ( 18 ). fill ( - 1 )); } // stores log values let logn = new Array ( 101 ). fill ( 0 ); // stores power of 2 let p2 = new Array ( 20 ). fill ( 0 ); function buildSparseTable ( n ) { // initializing sparse table for ( let i = 0 ; i < n ; i ++ ) { dp [ i ][ 0 ] = i - 1 >= 0 && depthArr [ i ] > depthArr [ i - 1 ] ? i - 1 : i ; } // dp to fill sparse table for ( let l = 1 ; l < 15 ; l ++ ) { for ( let i = 0 ; i < n ; i ++ ) { if ( dp [ i ][ l - 1 ] !== - 1 && dp [ i + p2 [ l - 1 ]][ l - 1 ] !== - 1 ) { dp [ i ][ l ] = depthArr [ dp [ i ][ l - 1 ]] > depthArr [ dp [ i + p2 [ l - 1 ]][ l - 1 ]] ? dp [ i + p2 [ l - 1 ]][ l - 1 ] : dp [ i ][ l - 1 ]; } else { break ; } } } } function query ( l r ) { let d = r - l ; let dx = logn [ d ]; if ( l === r ) { return l ; } if ( depthArr [ dp [ l ][ dx ]] > depthArr [ dp [ r - p2 [ dx ]][ dx ]]) { return dp [ r - p2 [ dx ]][ dx ]; } else { return dp [ l ][ dx ]; } } function preprocess () { // memorizing powers of 2 p2 [ 0 ] = 1 ; for ( let i = 1 ; i < 18 ; i ++ ) { p2 [ i ] = p2 [ i - 1 ] * 2 ; } // memorizing all log(n) values let val = 1 ; ptr = 0 ; for ( let i = 1 ; i < 101 ; i ++ ) { logn [ i ] = ptr - 1 ; if ( val === i ) { val *= 2 ; logn [ i ] = ptr ; ptr += 1 ; } } } function dfs ( cur prev dep ) { // marking FAI for cur node if ( FAI [ cur ] === - 1 ) { FAI [ cur ] = ptr ; } level [ cur ] = dep ; // pushing root to euler walk euler . push ( cur ); // incrementing euler walk pointer ptr += 1 ; for ( let x of adj [ cur ]) { if ( x !== prev ) { dfs ( x cur dep + 1 ); // pushing cur again in backtrack // of euler walk euler . push ( cur ); // increment euler walk pointer ptr += 1 ; } } } // Create Level depthArray corresponding // to the Euler walk Array function makeArr () { for ( let x of euler ) { depthArr . push ( level [ x ]); } } function LCA ( u v ) { // trivial case if ( u === v ) { return u ; } if ( FAI [ u ] > FAI [ v ]) { [ u v ] = [ v u ]; } // doing RMQ in the required range return euler [ query ( FAI [ u ] FAI [ v ])]; } function addEdge ( u v ) { adj [ u ]. push ( v ); adj [ v ]. push ( u ); } // constructing the described tree let numberOfNodes = 8 ; addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 2 4 ); addEdge ( 2 5 ); addEdge ( 2 6 ); addEdge ( 3 7 ); addEdge ( 3 8 ); // performing required precalculations preprocess (); // doing the Euler walk ptr = 0 ; FAI = new Array ( numberOfNodes + 1 ). fill ( - 1 ); dfs ( 1 0 0 ); // creating depthArray corresponding to euler[] makeArr (); // building sparse table buildSparseTable ( depthArr . length ); console . log ( 'LCA(67) : ' LCA ( 6 7 )); console . log ( 'LCA(64) : ' LCA ( 6 4 ));
Išvestis
LCA(67) : 1 LCA(64) : 2
Pastaba: Mes iš anksto apskaičiuojame visą reikiamą 2 galią ir taip pat iš anksto apskaičiuojame visas reikalingas log vertes, kad užtikrintume pastovų vienos užklausos laiko sudėtingumą. Priešingu atveju, jei atliktume kiekvienos užklausos operacijos žurnalo skaičiavimą, mūsų laiko sudėtingumas nebūtų buvęs pastovus.
Laiko sudėtingumas: Konvertavimo iš LCA į RMQ procesą atlieka Euler Walk, kuris užtrunka O(n) laiko.
Išankstinis retosios lentelės apdorojimas RMQ užtrunka O (nlogn) laiko, o atsakymas į kiekvieną užklausą yra nuolatinis procesas. Todėl bendras laiko sudėtingumas yra O(nlogn) – išankstinis apdorojimas ir O(1) kiekvienai užklausai.
Pagalbinė erdvė: O(n+s)
Sukurti viktoriną