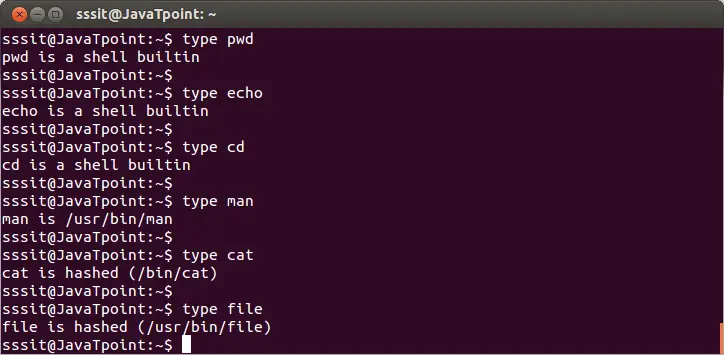
주어진 삼각형의 모든 각도 찾기

2D 평면에서 삼각형의 세 꼭지점 모두의 좌표가 주어지면 작업은 세 각도를 모두 찾는 것입니다.
예:
Input : A = (0 0) B = (0 1) C = (1 0) Output : 90 45 45
이 문제를 해결하기 위해 아래에서 사용합니다. 코사인의 법칙 .

c^2 = a^2 + b^2 - 2(a)(b)(cos beta)
다시 정리한 후
beta = acos( ( a^2 + b^2 - c^2 ) / (2ab) )
삼각법에서 코사인 법칙(코사인 공식 또는 코사인 법칙이라고도 함)은 삼각형 변의 길이를 각 각도 중 하나의 코사인과 연관시킵니다.
First calculate the length of all the sides. Then apply above formula to get all angles in radian. Then convert angles from radian into degrees.
다음은 위 단계의 구현입니다.
// Code to find all three angles // of a triangle given coordinate // of all three vertices #include #include // for pair #include // for math functions using namespace std ; #define PI 3.1415926535 // returns square of distance b/w two points int lengthSquare ( pair < int int > X pair < int int > Y ) { int xDiff = X . first - Y . first ; int yDiff = X . second - Y . second ; return xDiff * xDiff + yDiff * yDiff ; } void printAngle ( pair < int int > A pair < int int > B pair < int int > C ) { // Square of lengths be a2 b2 c2 int a2 = lengthSquare ( B C ); int b2 = lengthSquare ( A C ); int c2 = lengthSquare ( A B ); // length of sides be a b c float a = sqrt ( a2 ); float b = sqrt ( b2 ); float c = sqrt ( c2 ); // From Cosine law float alpha = acos (( b2 + c2 - a2 ) / ( 2 * b * c )); float beta = acos (( a2 + c2 - b2 ) / ( 2 * a * c )); float gamma = acos (( a2 + b2 - c2 ) / ( 2 * a * b )); // Converting to degree alpha = alpha * 180 / PI ; beta = beta * 180 / PI ; gamma = gamma * 180 / PI ; // printing all the angles cout < < 'alpha : ' < < alpha < < endl ; cout < < 'beta : ' < < beta < < endl ; cout < < 'gamma : ' < < gamma < < endl ; } // Driver code int main () { pair < int int > A = make_pair ( 0 0 ); pair < int int > B = make_pair ( 0 1 ); pair < int int > C = make_pair ( 1 0 ); printAngle ( A B C ); return 0 ; }
Java // Java Code to find all three angles // of a triangle given coordinate // of all three vertices import java.awt.Point ; import static java.lang.Math.PI ; import static java.lang.Math.sqrt ; import static java.lang.Math.acos ; class Test { // returns square of distance b/w two points static int lengthSquare ( Point p1 Point p2 ) { int xDiff = p1 . x - p2 . x ; int yDiff = p1 . y - p2 . y ; return xDiff * xDiff + yDiff * yDiff ; } static void printAngle ( Point A Point B Point C ) { // Square of lengths be a2 b2 c2 int a2 = lengthSquare ( B C ); int b2 = lengthSquare ( A C ); int c2 = lengthSquare ( A B ); // length of sides be a b c float a = ( float ) sqrt ( a2 ); float b = ( float ) sqrt ( b2 ); float c = ( float ) sqrt ( c2 ); // From Cosine law float alpha = ( float ) acos (( b2 + c2 - a2 ) / ( 2 * b * c )); float betta = ( float ) acos (( a2 + c2 - b2 ) / ( 2 * a * c )); float gamma = ( float ) acos (( a2 + b2 - c2 ) / ( 2 * a * b )); // Converting to degree alpha = ( float ) ( alpha * 180 / PI ); betta = ( float ) ( betta * 180 / PI ); gamma = ( float ) ( gamma * 180 / PI ); // printing all the angles System . out . println ( 'alpha : ' + alpha ); System . out . println ( 'betta : ' + betta ); System . out . println ( 'gamma : ' + gamma ); } // Driver method public static void main ( String [] args ) { Point A = new Point ( 0 0 ); Point B = new Point ( 0 1 ); Point C = new Point ( 1 0 ); printAngle ( A B C ); } }
Python3 # Python3 code to find all three angles # of a triangle given coordinate # of all three vertices import math # returns square of distance b/w two points def lengthSquare ( X Y ): xDiff = X [ 0 ] - Y [ 0 ] yDiff = X [ 1 ] - Y [ 1 ] return xDiff * xDiff + yDiff * yDiff def printAngle ( A B C ): # Square of lengths be a2 b2 c2 a2 = lengthSquare ( B C ) b2 = lengthSquare ( A C ) c2 = lengthSquare ( A B ) # length of sides be a b c a = math . sqrt ( a2 ); b = math . sqrt ( b2 ); c = math . sqrt ( c2 ); # From Cosine law alpha = math . acos (( b2 + c2 - a2 ) / ( 2 * b * c )); betta = math . acos (( a2 + c2 - b2 ) / ( 2 * a * c )); gamma = math . acos (( a2 + b2 - c2 ) / ( 2 * a * b )); # Converting to degree alpha = alpha * 180 / math . pi ; betta = betta * 180 / math . pi ; gamma = gamma * 180 / math . pi ; # printing all the angles print ( 'alpha : %f ' % ( alpha )) print ( 'betta : %f ' % ( betta )) print ( 'gamma : %f ' % ( gamma )) # Driver code A = ( 0 0 ) B = ( 0 1 ) C = ( 1 0 ) printAngle ( A B C ); # This code is contributed # by ApurvaRaj
C# // C# Code to find all three angles // of a triangle given coordinate // of all three vertices using System ; class GFG { class Point { public int x y ; public Point ( int x int y ) { this . x = x ; this . y = y ; } } // returns square of distance b/w two points static int lengthSquare ( Point p1 Point p2 ) { int xDiff = p1 . x - p2 . x ; int yDiff = p1 . y - p2 . y ; return xDiff * xDiff + yDiff * yDiff ; } static void printAngle ( Point A Point B Point C ) { // Square of lengths be a2 b2 c2 int a2 = lengthSquare ( B C ); int b2 = lengthSquare ( A C ); int c2 = lengthSquare ( A B ); // length of sides be a b c float a = ( float ) Math . Sqrt ( a2 ); float b = ( float ) Math . Sqrt ( b2 ); float c = ( float ) Math . Sqrt ( c2 ); // From Cosine law float alpha = ( float ) Math . Acos (( b2 + c2 - a2 ) / ( 2 * b * c )); float betta = ( float ) Math . Acos (( a2 + c2 - b2 ) / ( 2 * a * c )); float gamma = ( float ) Math . Acos (( a2 + b2 - c2 ) / ( 2 * a * b )); // Converting to degree alpha = ( float ) ( alpha * 180 / Math . PI ); betta = ( float ) ( betta * 180 / Math . PI ); gamma = ( float ) ( gamma * 180 / Math . PI ); // printing all the angles Console . WriteLine ( 'alpha : ' + alpha ); Console . WriteLine ( 'betta : ' + betta ); Console . WriteLine ( 'gamma : ' + gamma ); } // Driver Code public static void Main ( String [] args ) { Point A = new Point ( 0 0 ); Point B = new Point ( 0 1 ); Point C = new Point ( 1 0 ); printAngle ( A B C ); } } // This code is contributed by Rajput-Ji
JavaScript // JavaScript program // Code to find all three angles // of a triangle given coordinate // of all three vertices // returns square of distance b/w two points function lengthSquare ( X Y ){ let xDiff = X [ 0 ] - Y [ 0 ]; let yDiff = X [ 1 ] - Y [ 1 ]; return xDiff * xDiff + yDiff * yDiff ; } function printAngle ( A B C ){ // Square of lengths be a2 b2 c2 let a2 = lengthSquare ( B C ); let b2 = lengthSquare ( A C ); let c2 = lengthSquare ( A B ); // length of sides be a b c let a = Math . sqrt ( a2 ); let b = Math . sqrt ( b2 ); let c = Math . sqrt ( c2 ); // From Cosine law let alpha = Math . acos (( b2 + c2 - a2 ) / ( 2 * b * c )); let beta = Math . acos (( a2 + c2 - b2 ) / ( 2 * a * c )); let gamma = Math . acos (( a2 + b2 - c2 ) / ( 2 * a * b )); // Converting to degree alpha = alpha * 180 / Math . PI ; beta = beta * 180 / Math . PI ; gamma = gamma * 180 / Math . PI ; // printing all the angles console . log ( 'alpha : ' alpha ); console . log ( 'beta : ' beta ); console . log ( 'gamma : ' gamma ); } // Driver code let A = [ 0 0 ]; let B = [ 0 1 ]; let C = [ 1 0 ]; printAngle ( A B C ); // The code is contributed by Gautam goel (guatamgoel962)
산출:
alpha : 90 beta : 45 gamma : 45
시간 복잡도: 내장된 sqrt 함수를 사용한 이후 O(log(n))
보조 공간: 오(1)
참조 :
https://en.wikipedia.org/wiki/Law_of_cosines