유클리드 알고리즘(기본 및 확장)
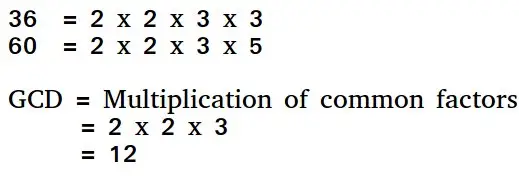
유클리드 알고리즘은 두 양의 정수의 최대 공약수를 찾는 방법입니다. 두 숫자의 GCD는 두 숫자를 나누는 가장 큰 숫자입니다. GCD를 구하는 간단한 방법은 두 숫자를 인수분해하고 공통 소인수를 곱하는 것입니다.
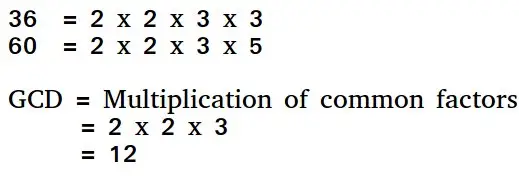
GCD에 대한 기본 유클리드 알고리즘:
알고리즘은 아래 사실을 기반으로 합니다.
- 큰 숫자에서 작은 숫자를 빼면(더 큰 숫자를 줄임) GCD는 변경되지 않습니다. 따라서 2개 중 더 큰 값을 계속해서 빼면 GCD가 됩니다.
- 이제 빼는 대신 더 작은 숫자를 나누면 나머지 0을 찾으면 알고리즘이 중지됩니다.
다음은 Euclid 알고리즘을 사용하여 gcd를 평가하는 재귀 함수입니다.
씨
// C program to demonstrate Basic Euclidean Algorithm> #include> // Function to return gcd of a and b> int> gcd(> int> a,> int> b)> {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> }> // Driver code> int> main()> {> > int> a = 10, b = 15;> > > // Function call> > printf> (> 'GCD(%d, %d) = %d
'> , a, b, gcd(a, b));> > a = 35, b = 10;> > printf> (> 'GCD(%d, %d) = %d
'> , a, b, gcd(a, b));> > a = 31, b = 2;> > printf> (> 'GCD(%d, %d) = %d
'> , a, b, gcd(a, b));> > return> 0;> }> |
CPP
// C++ program to demonstrate> // Basic Euclidean Algorithm> #include> using> namespace> std;> // Function to return> // gcd of a and b> int> gcd(> int> a,> int> b)> {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> }> // Driver Code> int> main()> {> > int> a = 10, b = 15;> > > // Function call> > cout < <> 'GCD('> < < a < <> ', '> < < b < <> ') = '> < < gcd(a, b)> > < < endl;> > a = 35, b = 10;> > cout < <> 'GCD('> < < a < <> ', '> < < b < <> ') = '> < < gcd(a, b)> > < < endl;> > a = 31, b = 2;> > cout < <> 'GCD('> < < a < <> ', '> < < b < <> ') = '> < < gcd(a, b)> > < < endl;> > return> 0;> }> |
자바
// Java program to demonstrate Basic Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> > // extended Euclidean Algorithm> > public> static> int> gcd(> int> a,> int> b)> > {> > if> (a ==> 0> )> > return> b;> > return> gcd(b % a, a);> > }> > // Driver code> > public> static> void> main(String[] args)> > {> > int> a => 10> , b => 15> , g;> > > // Function call> > g = gcd(a, b);> > System.out.println(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a => 35> ;> > b => 10> ;> > g = gcd(a, b);> > System.out.println(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a => 31> ;> > b => 2> ;> > g = gcd(a, b);> > System.out.println(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > }> }> // Code Contributed by Mohit Gupta_OMG> |
파이썬3
# Python3 program to demonstrate Basic Euclidean Algorithm> # Function to return gcd of a and b> def> gcd(a, b):> > if> a> => => 0> :> > return> b> > return> gcd(b> %> a, a)> # Driver code> if> __name__> => => '__main__'> :> > a> => 10> > b> => 15> > print> (> 'gcd('> , a,> ','> , b,> ') = '> , gcd(a, b))> > a> => 35> > b> => 10> > print> (> 'gcd('> , a,> ','> , b,> ') = '> , gcd(a, b))> > a> => 31> > b> => 2> > print> (> 'gcd('> , a,> ','> , b,> ') = '> , gcd(a, b))> # Code Contributed By Mohit Gupta_OMG> |
씨#
// C# program to demonstrate Basic Euclidean Algorithm> using> System;> class> GFG {> > public> static> int> gcd(> int> a,> int> b)> > {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> > }> > // Driver Code> > static> public> void> Main()> > {> > int> a = 10, b = 15, g;> > g = gcd(a, b);> > Console.WriteLine(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a = 35;> > b = 10;> > g = gcd(a, b);> > Console.WriteLine(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a = 31;> > b = 2;> > g = gcd(a, b);> > Console.WriteLine(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > }> }> // This code is contributed by ajit> |
PHP
// php program to demonstrate Basic Euclidean Algorithm> // PHP program to demonstrate // Basic Euclidean Algorithm // Function to return // gcd of a and b function gcd($a, $b) { if ($a == 0) return $b; return gcd($b % $a, $a); } // Driver Code $a = 10; $b = 15; // Function call echo 'GCD(',$a,',' , $b,') = ', gcd($a, $b); echo '
'; $a = 35; $b = 10; echo 'GCD(',$a ,',',$b,') = ', gcd($a, $b); echo '
'; $a = 31; $b = 2; echo 'GCD(',$a ,',', $b,') = ', gcd($a, $b); // This code is contributed by m_kit ?>> |
자바스크립트
// JavaScript program to demonstrate> // Basic Euclidean Algorithm> // Function to return> // gcd of a and b> function> gcd( a, b)> {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> }> // Driver Code> > let a = 10, b = 15;> > document.write(> 'GCD('> + a +> ', '> > + b +> ') = '> + gcd(a, b) +> ' '> );> > > a = 35, b = 10;> > document.write(> 'GCD('> + a +> ', '> > + b +> ') = '> + gcd(a, b) +> ' '> );> > > a = 31, b = 2;> > document.write(> 'GCD('> + a +> ', '> > + b +> ') = '> + gcd(a, b) +> ' '> );> // This code contributed by aashish1995> |
산출
GCD(10, 15) = 5 GCD(35, 10) = 5 GCD(31, 2) = 1
시간 복잡도: O(로그 최소(a, b))
보조 공간: O(로그(최소(a,b))
확장된 유클리드 알고리즘:
확장된 유클리드 알고리즘은 또한 다음과 같은 정수 계수 x와 y를 찾습니다. ax + by = gcd(a, b)
예:
입력: a = 30, b = 20
산출: gcd = 10, x = 1, y = -1
(30*1 + 20*(-1) = 10이라는 점에 유의하세요.)입력: a = 35, b = 15
산출: gcd = 5, x = 1, y = -2
(35*1 + 15*(-2) = 5라는 점에 유의하세요.)
확장된 유클리드 알고리즘은 재귀 호출 gcd(b%a, a)에 의해 계산된 결과를 사용하여 gcd(a, b)의 결과를 업데이트합니다. 재귀 호출로 계산된 x와 y의 값을 x로 둡니다. 1 그리고 y 1 . x와 y는 아래 표현식을 사용하여 업데이트됩니다.
추천 실습 확장 유클리드 알고리즘 시도해 보세요!ax + by = gcd(a, b)
gcd(a, b) = gcd(b%a, a)
gcd(b%a, a) = (b%a)x 1 +는 1
도끼 + 에 의해 = (b%a)x 1 +는 1
ax + by = (b – [b/a] * a)x 1 +는 1
도끼 + by = a(y 1 – [b/a] * x 1 ) + bx 1LHS와 RHS를 비교하면,
x = y 1 – ?b/a? * x 1
와이 = 엑스 1
다음은 위의 접근 방식을 구현한 것입니다.
C++
// C++ program to demonstrate working of> // extended Euclidean Algorithm> #include> using> namespace> std;> // Function for extended Euclidean Algorithm> int> gcdExtended(> int> a,> int> b,> int> *x,> int> *y)> {> > // Base Case> > if> (a == 0)> > {> > *x = 0;> > *y = 1;> > return> b;> > }> > int> x1, y1;> // To store results of recursive call> > int> gcd = gcdExtended(b%a, a, &x1, &y1);> > // Update x and y using results of> > // recursive call> > *x = y1 - (b/a) * x1;> > *y = x1;> > return> gcd;> }> // Driver Code> int> main()> {> > int> x, y, a = 35, b = 15;> > int> g = gcdExtended(a, b, &x, &y);> > cout < <> 'GCD('> < < a < <> ', '> < < b> > < <> ') = '> < < g < < endl;> > return> 0;> }> |
씨
// C program to demonstrate working of extended> // Euclidean Algorithm> #include> // C function for extended Euclidean Algorithm> int> gcdExtended(> int> a,> int> b,> int> *x,> int> *y)> {> > // Base Case> > if> (a == 0)> > {> > *x = 0;> > *y = 1;> > return> b;> > }> > int> x1, y1;> // To store results of recursive call> > int> gcd = gcdExtended(b%a, a, &x1, &y1);> > // Update x and y using results of recursive> > // call> > *x = y1 - (b/a) * x1;> > *y = x1;> > return> gcd;> }> // Driver Program> int> main()> {> > int> x, y;> > int> a = 35, b = 15;> > int> g = gcdExtended(a, b, &x, &y);> > printf> (> 'gcd(%d, %d) = %d'> , a, b, g);> > return> 0;> }> |
자바
// Java program to demonstrate working of extended> // Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> > // extended Euclidean Algorithm> > public> static> int> gcdExtended(> int> a,> int> b,> int> x,> > int> y)> > {> > // Base Case> > if> (a ==> 0> ) {> > x => 0> ;> > y => 1> ;> > return> b;> > }> > int> x1 => 1> ,> > y1 => 1> ;> // To store results of recursive call> > int> gcd = gcdExtended(b % a, a, x1, y1);> > // Update x and y using results of recursive> > // call> > x = y1 - (b / a) * x1;> > y = x1;> > return> gcd;> > }> > // Driver Program> > public> static> void> main(String[] args)> > {> > int> x => 1> , y => 1> ;> > int> a => 35> , b => 15> ;> > int> g = gcdExtended(a, b, x, y);> > System.out.print(> 'gcd('> + a +> ' , '> + b> > +> ') = '> + g);> > }> }> |
파이썬3
# Python program to demonstrate working of extended> # Euclidean Algorithm> # function for extended Euclidean Algorithm> def> gcdExtended(a, b):> > # Base Case> > if> a> => => 0> :> > return> b,> 0> ,> 1> > gcd, x1, y1> => gcdExtended(b> %> a, a)> > # Update x and y using results of recursive> > # call> > x> => y1> -> (b> /> /> a)> *> x1> > y> => x1> > return> gcd, x, y> # Driver code> a, b> => 35> ,> 15> g, x, y> => gcdExtended(a, b)> print> (> 'gcd('> , a,> ','> , b,> ') = '> , g)> |
씨#
// C# program to demonstrate working> // of extended Euclidean Algorithm> using> System;> class> GFG> {> > > // extended Euclidean Algorithm> > public> static> int> gcdExtended(> int> a,> int> b,> > int> x,> int> y)> > {> > // Base Case> > if> (a == 0)> > {> > x = 0;> > y = 1;> > return> b;> > }> > // To store results of> > // recursive call> > int> x1 = 1, y1 = 1;> > int> gcd = gcdExtended(b % a, a, x1, y1);> > // Update x and y using> > // results of recursive call> > x = y1 - (b / a) * x1;> > y = x1;> > return> gcd;> > }> > > // Driver Code> > static> public> void> Main ()> > {> > int> x = 1, y = 1;> > int> a = 35, b = 15;> > int> g = gcdExtended(a, b, x, y);> > Console.WriteLine(> 'gcd('> + a +> ' , '> +> > b +> ') = '> + g);> > }> }> |
PHP
// PHP program to demonstrate // working of extended // Euclidean Algorithm // PHP function for // extended Euclidean // Algorithm function gcdExtended($a, $b, $x, $y) { // Base Case if ($a == 0) { $x = 0; $y = 1; return $b; } // To store results // of recursive call $gcd = gcdExtended($b % $a, $a, $x, $y); // Update x and y using // results of recursive // call $x = $y - floor($b / $a) * $x; $y = $x; return $gcd; } // Driver Code $x = 0; $y = 0; $a = 35; $b = 15; $g = gcdExtended($a, $b, $x, $y); echo 'gcd(',$a; echo ', ' , $b, ')'; echo ' = ' , $g; ?>> |
자바스크립트
> // Javascript program to demonstrate> // working of extended> // Euclidean Algorithm> // Javascript function for> // extended Euclidean> // Algorithm> function> gcdExtended(a, b,> > x, y)> {> > // Base Case> > if> (a == 0)> > {> > x = 0;> > y = 1;> > return> b;> > }> > // To store results> > // of recursive call> > let gcd = gcdExtended(b % a,> > a, x, y);> > // Update x and y using> > // results of recursive> > // call> > x = y - (b / a) * x;> > y = x;> > return> gcd;> }> // Driver Code> let x = 0;> let y = 0;> let a = 35;> let b = 15;> let g = gcdExtended(a, b, x, y);> document.write(> 'gcd('> + a);> document.write(> ', '> + b +> ')'> );> document.write(> ' = '> + g);> > |
출력 :
gcd(35, 15) = 5
시간 복잡도: 오(로그 N)
보조 공간: 오(로그 N)
확장 알고리즘은 어떻게 작동하나요?
위에서 볼 수 있듯이 x와 y는 입력 a와 b에 대한 결과입니다.
a.x + b.y = gcd —-(1)
그리고 x 1 그리고 y 1 입력 b%a 및 a에 대한 결과입니다.
(b%a).x 1 + 에이 1 = gcd
위에 b%a = (b – (?b/a?).a) 를 넣으면,
우리는 따라옵니다. ?b/a? 층(b/a)입니다(b – (?b/a?).a).x 1 + 에이 1 = gcd
위의 방정식은 다음과 같이 쓸 수도 있습니다.
b.x 1 + a.(그리고 1 – (?b/a?).x 1 ) = gcd —(2)
(1)에서 'a'와 'b'의 계수를 비교한 후
(2), 우리는 다음과 같은 결과를 얻습니다.
x = y 1 – ?b/a? * x 1
와이 = 엑스 1
확장 알고리즘은 어떻게 유용합니까?
확장된 유클리드 알고리즘은 a와 b가 서로소일 때(또는 gcd가 1일 때) 특히 유용합니다. x는 모듈로 b의 모듈러 곱셈 역이고, y는 b 모듈로 a의 모듈러 곱셈 역이기 때문입니다. 특히, 모듈러 곱셈 역원의 계산은 RSA 공개키 암호화 방법에서 필수적인 단계입니다.