코탄젠트 공식

삼각법은 직각삼각형의 변의 길이와 각도 사이의 관계를 다루는 수학의 중요한 분야입니다. 사인, 코사인, 탄젠트, 코시컨트, 시컨트 및 코탄젠트는 6개의 삼각비 또는 함수입니다. 삼각비는 직각 삼각형의 변 사이의 비율로 표시됩니다.

sin θ = 대변/빗변
cos θ = 인접변/빗변
tan θ = 반대쪽/인접한 쪽
cosec θ = 1/sin θ = 빗변/대변
초 θ = 1/cos θ = 빗변/인접변
cot θ = 1/tan θ = 인접면/반대면

코탄젠트 함수는 주어진 탄젠트 함수의 역함수입니다. 직각삼각형의 코탄젠트각의 값은 주어진 각도에 인접한 변의 길이와 주어진 각도에 반대되는 변의 길이의 비율입니다. cot로 코탄젠트 함수를 작성합니다.

삼각형 ABC

이제 각도 θ에 대한 코탄젠트 공식은 다음과 같습니다.

cot θ = (인접한 쪽)/(반대쪽)

코탄젠트 함수는 첫 번째 및 세 번째 사분면에서는 양수이고 두 번째 및 네 번째 사분면에서는 음수입니다.

cot (2π + θ) = cot θ (1 ^성 사분면)
cot (π – θ) = – cot θ (2 ^nd 사분면)
cot (π + θ) = cot θ (3) ^rd 사분면)
cot (2π – θ) = – cot θ (4 ^일 사분면)

코탄젠트 함수는 음의 각도의 코탄젠트가 코탄젠트 양의 각도의 음수이기 때문에 음의 함수입니다.

cot (-θ) = - cot θ

탄젠트 함수의 관점에서 코탄젠트 함수는 다음과 같이 작성됩니다.

cot θ = 1/tan θ

(또는)

cot θ = tan (90° – θ) (또는) tan (π/2 – θ)

사인 및 코사인 함수의 코탄젠트 함수는 다음과 같이 작성할 수 있습니다.

cot θ = cos θ/sin θ

우리는 cot θ = 인접한 변/반대 변이라는 것을 알고 있습니다.

이제 빗변으로 분자와 분모를 모두 나눕니다.

⇒ cot θ = (인접한 변/빗변) / (반대 변/빗변)

우리는 sin θ = 대변/빗변이라는 것을 알고 있습니다.

cos θ = 인접변/빗변

따라서 cot θ = cos θ/sin θ

사인 함수의 코탄젠트 함수는 다음과 같이 쓸 수 있습니다.

cot θ = (√1 – 죄 ² i)/sin i

우리는 cot θ = cos θ/sin θ라는 것을 알고 있습니다.

피타고라스의 정체성으로부터 우리는;

코사인 ² θ + 죄 ² θ = 1

⇒ cos θ = √1 – 죄 ² 나

따라서 cot θ = $frac{sqrt{left(1-sin^{2} heta ight)}}{sin heta}$

코사인 함수의 코탄젠트 함수는 다음과 같이 쓸 수 있습니다.

cot θ = cos θ/(√1 -cos ² 나)

우리는 cot θ = cos θ/sin θ라는 것을 알고 있습니다.

피타고라스의 정체성으로부터 우리는;

코사인 ² θ + 죄 ² θ = 1

죄 θ = √1 – cos ² 나

따라서 cot θ = $frac{cos heta}{sqrt{left(1-cos^{2} heta ight)}}$

시컨트 및 코시컨트 함수 측면에서 코탄젠트 함수는 다음과 같이 작성할 수 있습니다.

cot θ = cosec θ/초 θ

cot θ = cos θ/sin θ

이는 다음과 같이 쓸 수 있습니다. cot θ = (1/sin θ) / (1/cos θ)

⇒ cot θ = cosec θ/초 θ

코시컨트 함수의 관점에서 코탄젠트 함수는 다음과 같이 작성할 수 있습니다.

cot θ = √(cosec ² - 1)

피타고라스 항등식으로부터 우리는,

코섹 ² θ – 유아용 침대 ² θ = 1

⇒ 유아용 침대 ² θ = 1 - 코초 ² - 1

따라서 cot θ = √(cosec ² - 1)

시컨트 함수 측면에서 코탄젠트 함수는 다음과 같이 작성할 수 있습니다.

cot θ = 1/(√sec ² 나 – 1)

피타고라스 항등식으로부터 우리는,

비서 ² θ – 그래서 ² θ = 1

탄젠트 θ = √초 ² 나 – 1

우리는 cot θ = 1/tan θ라는 것을 알고 있습니다.

따라서, 침대 θ = $frac{1}{sqrt{left(1초^{2} heta ight)}}$

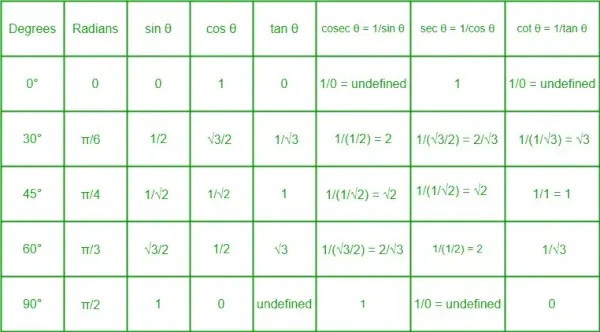
삼각비 테이블

삼각비표

코탄젠트 법칙 또는 코탄젠트 법칙

코탄젠트 법칙은 사인 법칙과 유사해 보이지만 여기서는 반각이 포함됩니다. 코탄젠트의 법칙은 삼각형의 변의 길이와 세 각의 절반의 코탄젠트 사이의 관계를 설명합니다. a, b, c가 삼각형 변의 길이인 삼각형 ABC를 생각해 보세요.

코탄젠트의 법칙에 따르면,

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

여기서 s는 삼각형 ABC의 반둘레이고 r은 삼각형 내접원의 반경입니다.

s = (a + b + c)/2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

샘플 문제

문제 1: tan θ = 3/4일 때 cot θ 값을 구하세요.

해결책:

주어진 데이터에서 tan θ = 3/4

우리는 그것을 알고 있습니다. cot θ = 1/tan θ

⇒ 침대 θ = 1/(3/4) = 4/3

따라서 cot θ = 4/3

문제 2: cot α, sin α = 1/3, cos α = 2√2/3의 값을 구하세요.

해결책:

주어진 데이터에서 sin α = 1/3이고 cos α = 2√2/3입니다.

우리는 그것을 알고 있습니다. cot α = cos α/sin α

⇒ 면 α = (2√2/3) / (1/3) = 2√2

따라서 cot α = 2√2의 값

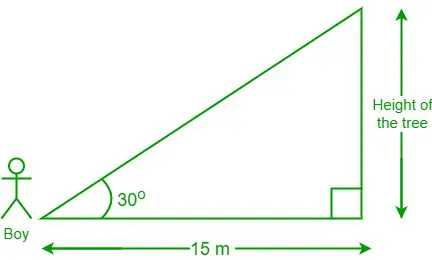
문제 3: 나무에서 15m 떨어진 곳에 서있는 소년이 나무 꼭대기를 30도 각도로 바라보고 있습니다. 나무의 높이는 얼마입니까?

해결책:

주어진 데이터의 다이어그램

주어진 데이터에서 소년과 나무 밑 사이의 거리는 15m이고 θ = 30°입니다.

트리의 높이를 'h'로 둡니다.

우리는 cot θ = 인접면/반대면

⇒ 유아용 침대 30° = 15/h

⇒ √3 = 15/h [이후, cot 30° = √3]

⇒ h = 15/√3

⇒ h = 5√3m

따라서 나무의 높이는 5√3m

문제 4: sec x = 6/5일 때 cot x의 값을 구하세요.

해결책:

주어진 데이터, 초 x = 6/5

우리는 비서 ² x – 그래서 ² 엑스 = 1

⇒ (6/5) ² - 그래서 ² 엑스 = 1

⇒ 36/25 – 그래서 ² 엑스 = 1

⇒ 그래서 ² x = 36/25 – 1

⇒ 그래서 ² x = 11/25

⇒ tan x = √(11/25) = √11/5

우리는 그것을 알고 있습니다. 유아용 x = 1/황갈색 x

⇒ cot x = 1/(√11/5) = 5/√11

따라서 cot x = 5/√11

문제 5: cosec θ = 25/24일 때 cot θ 값을 구하세요.

해결책:

주어진 데이터에서 cosec θ = 25/24

우리는 그것을 알고 있습니다. cot θ = √(cosec ² - 1)

⇒ 침대 θ = √(25/24) ² - 1

⇒ 면 θ =√(625 – 576)/576 = √49/576

⇒ 유아용 침대 θ = 7/24

따라서 cot θ = 7/24의 값

문제 6: sin β = 5/13일 때 cot β의 값을 구하세요.

해결책:

주어진 데이터에서 sin β = 5/13

우리는 그것을 알고 있습니다. 없이 ² β + 왜냐하면 ² β = 1

⇒ (5/13) ² + 왜냐하면 ² β = 1

⇒ 왜냐하면 ² β = 1 – (5/13) ² = 1 – 25/169 = 144/169

⇒ cos β = √144/169 = 12/13

cot β = cosβ/sin β

= (12/13) / (5/13)

⇒ 유아용 침대 β = 12/5

따라서 cot β = 12/5의 값

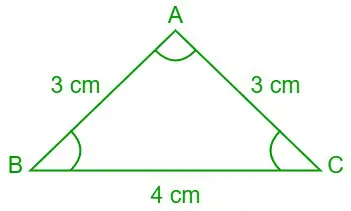
문제 7: 코탄젠트의 법칙을 사용하여 삼각형 ABC의 세 변의 길이가 a = 4 cm, b= 3 cm, c=일 때 ∠A, ∠B, ∠C의 값(도)을 구하십시오. 3cm.

해결책:

주어진 경우, a = 4cm, b = 3cm 및 c = 3cm

삼각형 ABC

코탄젠트 법칙으로부터,

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

s = (a + b + c)/2

⇒ s = (3 + 4 + 3)/2 = 10/2 = 5

이제 s – a = 5 – 4 = 1

⇒ s – b = 5 – 3 = 2

⇒ s – c = 5 – 3 = 2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

⇒ r = √[(1)(2)(2)/5]

삼각형의 반경 r = 2/√5

코탄젠트 법칙의 방정식으로부터,

cot (A/2)/1 = 1/(2/√5)

⇒ 유아용 침대 (A/2) = √5/2 ⇒ A/2 = 유아용 침대 ^-1 (√5/2)

⇒ (A/2) = 41.8° ⇒ ∠A = 83.6°

cot(B/2)/2 = 1/(2/√5)

⇒ 단(B/2)/2 = √5/2 ⇒ 단(B/2) = √5

⇒ (B/2) = 유아용 침대 ^-1 (√5) = 24.1° ⇒ ∠B = 48.2°

cot (C/2)/2 = 1/(2/√5)

⇒ cot(C/2) = √5 ⇒ (C/2) = cot ^-1 (√5)

⇒ (C/2) = 24.1° ⇒ ∠C = 48.2°

따라서 삼각형 ABC의 각도는 ∠A = 83.6°, ∠B = 48.2° 및 ∠C = 48.2°입니다.