二分探索木 (BST) での検索

与えられた BST 、タスクはこの中でノードを検索することです BST 。

BST で値を検索する場合は、それをソートされた配列とみなしてください。これで、次を使用して BST で検索操作を簡単に実行できるようになりました。 二分探索アルゴリズム 。

指定された二分探索ツリーでキーを検索するアルゴリズム:

番号を検索したいとしましょう バツ、 根元から始めます。それから：

検索する値とルートの値を比較します。
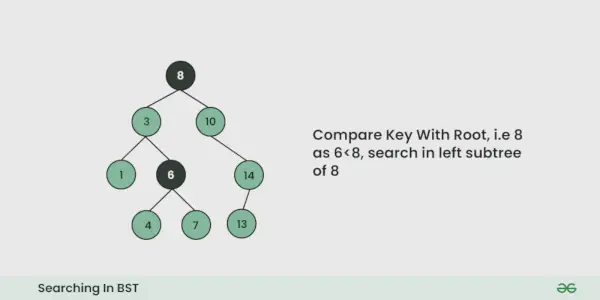
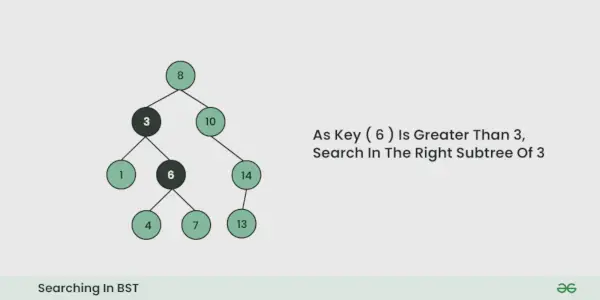
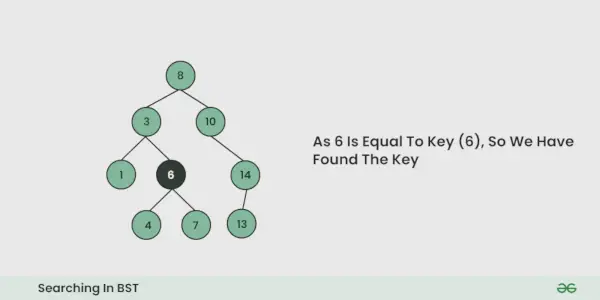
- 等しい場合、検索は終了します。小さい場合、二分探索ツリーでは、左側のサブツリーのすべての要素が小さく、右側のサブツリーのすべての要素が大きいため、左側のサブツリーに進む必要があることがわかります。
横断が不可能になるまで上記の手順を繰り返します
いずれかの反復でキーが見つかった場合は、True を返します。それ以外の場合は偽です。

BST での検索の図:

よりよく理解するには、以下の図を参照してください。

推奨される実践方法 BSTT でノードを検索してみよう!

BST で検索を実装するプログラム:

C++

// C++ function to search a given key in a given BST> #include> using> namespace> std;> struct> node {> > int> key;> > struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(> int> item)> {> > struct> node* temp> > => new> struct> node;> > temp->キー = アイテム;>>' < < endl;> > else> > cout < < key < <> ' found'> < < endl;> > key = 60;> > // Searching in a BST> > if> (search(root, key) == NULL)> > cout < < key < <> ' not found'> < < endl;> > else> > cout < < key < <> ' found'> < < endl;> > return> 0;> }>

C

// C function to search a given key in a given BST> #include> #include> struct> node {> > int> key;> > struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(> int> item)> {> > struct> node* temp> > = (> struct> node*)> malloc> (> sizeof> (> struct> node));> > temp->キー = アイテム;>>' , key);> > else> > printf> (>

'%d found
'>

, key);> > key = 60;> > // Searching in a BST> > if> (search(root, key) == NULL)> > printf> (>

'%d not found
'>

, key);> > else> > printf> (>

'%d found
'>

, key);> > return> 0;> }>

ジャワ

// Java program to search a given key in a given BST> class> Node {> > int> key;> > Node left, right;> > public> Node(> int> item) {> > key = item;> > left = right => null> ;> > }> }> class> BinarySearchTree {> > Node root;> > // Constructor> > BinarySearchTree() {> > root => null> ;> > }> > // A utility function to insert> > // a new node with given key in BST> > Node insert(Node node,> int> key) {> > // If the tree is empty, return a new node> > if> (node ==> null> ) {> > node => new> Node(key);> > return> node;> > }> > // Otherwise, recur down the tree> > if>

(key   node.left = insert(node.left, key);  else if (key>ノード.キー) ノード.右 = 挿入(ノード.ライト, キー);  // (変更されていない) ノード ポインタを返します。 return ノード;  } // BST でキーを検索するユーティリティ関数 Node search(Node root, int key) // ドライバー コード public static void main(String[] args) { BinarySearchTreetree = new BinarySearchTree();  // ノードを挿入しますtree.root =tree.insert(tree.root, 50);  ツリー.インサート(ツリー.ルート, 30);  ツリー.インサート(ツリー.ルート, 20);  ツリー.インサート(ツリー.ルート, 40);  ツリー.インサート(ツリー.ルート, 70);  ツリー.インサート(ツリー.ルート, 60);  ツリー.インサート(ツリー.ルート, 80);  // 検索するキー int key = 6;  // BST での検索 if (tree.search(tree.root, key) == null) System.out.println(key + ' not found');  else System.out.println(key + ' found');  キー = 60;  // BST での検索 if (tree.search(tree.root, key) == null) System.out.println(key + ' not found');  else System.out.println(key + ' found');  } }>>

Python3

# Python3 function to search a given key in a given BST> class> Node:> > # Constructor to create a new node> > def> __init__(> self> , key):> > self> .key> => key> > self> .left> => None> > self> .right> => None> # A utility function to insert> # a new node with the given key in BST> def> insert(node, key):> > # If the tree is empty, return a new node> > if> node> is> None> :> > return> Node(key)> > # Otherwise, recur down the tree> > if>

key   node.left = insert(node.left, key)  elif key>node.key:node.right = insert(node.right, key) # (変更されていない) ノード ポインターを返します return node # BST でキーを検索するユーティリティ関数 def search(root, key): # 基本ケース: root はroot が None または root.key == key の場合、null またはキーが root に存在します。 return root # root.key の場合、キーは root のキーより大きいです return search(root.right, key) # キーは root より小さいです のキー return search(root.left, key) # ドライバー コード if __name__ == '__main__': root = None root = insert(root, 50) insert(root, 30) insert(root, 20) insert (root, 40) insert(root, 70) insert(root, 60) insert(root, 80) # 検索するキー key = 6 # search(root, key) が None の場合の BST での検索: print(key, 'not found') else: print(key, 'found') key = 60 # search(root, key) が None の場合、BST で検索します: print(key, 'not found') else: print(key, 'found')>>

C#

// C# function to search a given key in a given BST> using> System;> public> class> Node {> > public> int> key;> > public> Node left, right;> }> public> class> BinaryTree {> > // A utility function to create a new BST node> > public> Node NewNode(> int> item)> > {> > Node temp => new> Node();> > temp.key = item;> > temp.left = temp.right => null> ;> > return> temp;> > }> > // A utility function to insert> > // a new node with given key in BST> > public> Node Insert(Node node,> int> key)> > {> > // If the tree is empty, return a new node> > if> (node ==> null> )> > return> NewNode(key);> > // Otherwise, recur down the tree> > if>

(key   node.left = Insert(node.left, key);  else if (key>ノード.キー) ノード.右 = 挿入(ノード.ライト, キー);  // (変更されていない) ノード ポインタを返します。 return ノード;  } // BST 内のキーを検索するユーティリティ関数 public Node Search(Node root, int key) // 基本ケース: ルートが null またはキーがルートに存在する if (root == null // ドライバー コード public static void Main () { BinaryTree bt = new BinaryTree(); bt.Insert(root, 30); , 40); bt.Insert(root, 60); // 検索するキー int key = 6; bt.Search(root, key) == null) Console.WriteLine(key + ' not found'); else Console.WriteLine(key + ' found'); // BST 内を検索します。 if (bt.Search(root, key) == null) Console.WriteLine(key + ' not found'); else Console.WriteLine(key + ' found');

>    
      
      
       
   
       
       
     
     
   
          // Javascript function to search a given key in a given BST>   class Node {>   >  constructor(key) {>   >  this>  .key = key;>   >  this>  .left =>  null>  ;>   >  this>  .right =>  null>  ;>   >  }>   }>   // A utility function to insert>   // a new node with given key in BST>   function>   insert(node, key) {>   >  // If the tree is empty, return a new node>   >  if>   (node ===>  null>  ) {>   >  return>   new>   Node(key);>   >  }>   >  // Otherwise, recur down the tree>   >  if>   (key   node.left = insert(node.left, key);  } else if (key>ノード.キー) { ノード.右 = 挿入(ノード.右, キー);  } // (変更されていない) ノード ポインタを返します return node; } // BST 関数でキーを検索するユーティリティ関数 search(root, key) { // 基本ケース: ルートが null またはキーがルートに存在する if (root === null || root.key === key ) { ルートを返す;  } // キーがルートのキーより大きい if (root.key return search(root.right, key); } // キーがルートのキーより小さい return search(root.left, key); } // ドライバー コード let root = null; insert(root, 30); insert(root, 70); 60); insert(root, 80); // 検索するキー let key = 6 // BST での検索 if (search(root, key) === null) { console.log(key + ' not) found'); } else { console.log(key + ' found') } key = 60; // BST での検索 if (search(root, key) === null) { console.log(キー + ' 見つかりません'); } else { console.log(key + ' 見つかりません') }>    
  
  
   
      
    
      
    
  出力    
  6 not found 60 found 
      時間計算量:     O(h)、ここで h は BST の高さです。   
    補助スペース:     O(h)、ここで h は BST の高さです。これは、再帰スタックを保存するために必要な最大スペース量が次のとおりであるためです。     h     。  
      関連リンク：        
       二分探索ツリー挿入操作    
    二分探索木の削除操作