線形探索と二分探索の違いを理解する前に、まず線形探索と二分探索を別々に理解する必要があります。

線形探索とは何ですか?

線形検索は、一度に各要素を単純にスキャンする順次検索とも呼ばれます。配列またはリスト内の要素を検索するとします。単に長さを計算するだけで、どの項目にもジャンプしません。

簡単な例を考えてみましょう。

次の図に示すように、10 個の要素からなる配列があるとします。

上の図は、10 個の値を持つ文字型の配列を示しています。 「E」を検索したい場合、検索は 0 から始まります。 ^番目 要素を検索し、要素 (つまり「E」) が見つからなくなるまで各要素をスキャンします。 0から直接ジャンプすることはできません ^番目 要素を 4 に ^番目 つまり、要素が見つからなくなるまで各要素が 1 つずつスキャンされます。

線形探索の複雑さ

線形検索では、要素が見つからなくなるまで各要素を 1 つずつスキャンします。要素数が増加すると、スキャンする要素の数も増加します。言えることは、 要素の検索にかかる時間は要素の数に比例します 。したがって、最悪の場合の複雑さは O(n) です。

二分探索とは何ですか?

二分探索とは、中央の要素を計算し、検索対象の要素より小さいか大きいかを調べる検索です。二分検索を使用する主な利点は、リスト内の各要素をスキャンしないことです。各要素をスキャンする代わりに、リストの半分まで検索を実行します。したがって、二分探索は線形探索と比較して要素の検索にかかる時間が短くなります。

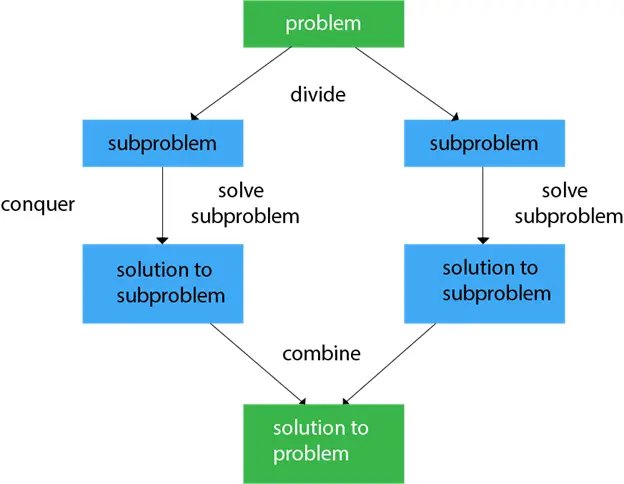
それ 二分探索の前提条件 それは、配列はソートされた順序である必要があるのに対し、線形検索はソートされた配列とソートされていない配列の両方で機能するということです。二分探索アルゴリズムは分割統治法に基づいており、配列を再帰的に分割します。

二分探索では 3 つのケースが使用されます。

ケース 1: データ

ケース 2: data>a[mid] の場合、right=mid-1

ケース 3: data = a[mid] // 要素が見つかった

上記の場合、「 ある ' は配列の名前です。 半ば 再帰的に計算される要素のインデックスです。 データ は検索される要素です。 左 は配列の左側の要素を示し、 右 は配列の右側にある要素を示します。

例を通して二分探索の仕組みを理解しましょう。

以下の図に示すように、0 から 9 までのインデックスが付けられたサイズ 10 の配列があるとします。

上記の配列から 70 個の要素を検索したいとします。

ステップ1： まず、配列の中央の要素を計算します。 2 つの変数、つまり左と右を考慮します。以下の図に示すように、最初は左 =0、右 =9 です。

中間要素の値は次のように計算できます。

したがって、mid = 4、a[mid] = 50となります。検索対象の要素は70であるため、a[mid]はdataと等しくありません。ケース 2 は満たされます。つまり、data > a[mid] です。

ステップ2： data>a[mid] であるため、left の値はmid+1 ずつ増加します。つまり、left=mid+1 となります。 Mid の値は 4 なので、left の値は 5 になります。これで、以下の図に示すような部分配列が得られました。

ここでも、上記の式を使用して中間値が計算され、mid の値は 7 になります。ここで、mid は次のように表すことができます。

上の図では、a[mid]>data であることがわかります。したがって、やはり次のステップで Mid の値が計算されます。

ステップ 3: a[mid]>dataとして、rightの値がmid-1だけ減らされます。 Mid の値は 7 なので、right の値は 6 になります。配列は次のように表すことができます。

Mid の値が再計算されます。 left と right の値はそれぞれ 5 と 6 です。したがって、mid の値は 5 です。これで、mid は以下に示すように配列で表すことができます。

上の図では、a[mid] が確認できます。

ステップ 4: [中]として

ここで、mid の値は、すでに説明した式を使用して再計算されます。以下の図に示すように、left と right の値はそれぞれ 6 と 6 であるため、mid の値は 6 になります。

上の図では、a[mid]=data であることがわかります。したがって、検索は完了し、要素は正常に見つかります。

線形探索と二分探索の違い

線形検索と二分検索の違いは次のとおりです。

説明

線形検索は、リスト内で要素が見つかるまで要素を順番に検索することで、リスト内の要素を見つける検索です。一方、二分探索は、リスト内の中央の要素が検索された要素と一致するまで再帰的に検索する検索です。

両方の検索の動作

線形検索は、最初の要素から検索を開始し、次の要素にジャンプすることなく、一度に 1 つの要素をスキャンします。一方、二分探索では、配列の中央の要素を計算して配列を半分に分割します。

実装

線形検索は、ベクトル、単一リンク リスト、二重リンク リストなどの任意の線形データ構造に対して実装できます。対照的に、二分探索は双方向トラバーサル、つまり前方および後方トラバーサルを使用してデータ構造に実装できます。

複雑

線形探索は使いやすい、または線形探索では要素を任意の順序で配置できるため、複雑さが少ないと言えますが、二分探索では要素を特定の順序で配置する必要があります。

並べ替えられた要素

線形探索の要素はランダムな順序で配置できます。線形検索では、要素がソートされた順序で配置されることは必須ではありません。一方、二分探索では、要素をソート順に並べる必要があります。昇順でも降順でも並べることができ、それに応じてアルゴリズムが変わります。二分探索ではソートされた配列を使用するため、適切な位置に要素を挿入する必要があります。対照的に、線形検索では並べ替えられた配列が必要ないため、新しい要素を配列の最後に簡単に挿入できます。

アプローチ

線形検索は反復アプローチを使用して要素を見つけるため、逐次アプローチとも呼ばれます。対照的に、二分探索では配列の中央の要素が計算されるため、分割統治アプローチが使用されます。

データセット

線形検索は大規模なデータセットには適していません。配列の最後の要素を検索したい場合、線形検索では最初の要素から検索を開始し、最後の要素まで検索するため、要素の検索に時間がかかります。一方、二分探索は時間がかからないため、大規模なデータセットに適しています。

スピード

線形探索ではデータセットが大きいと計算コストが高くなり、速度が遅くなります。二分探索ではデータセットが大きい場合、線形探索に比べて計算量が少なく、速度が速くなります。

寸法

線形探索は 1 次元配列と多次元配列の両方で使用できますが、二分探索は 1 次元配列でのみ実装できます。

効率

線形検索は、大規模なデータセットを考慮すると効率が低くなります。データセットが大きい場合、二分探索は線形探索よりも効率的です。

違いを表形式で見てみましょう。