n 進木の LCA |定数クエリ O(1)
n 分ツリーで LCA を計算するために、異なる時間計算量を使用するさまざまな方法を見てきました。
方法 1 : 単純な方法 (ルートからノードへのパスを計算することによる) |クエリあたり O(n)
方法 2 : Sqrt 分解の使用 | O(平方H)
方法 3 : スパース行列 DP アプローチの使用 | O(ログン)
上記のすべての方法よりもクエリ時間が速い別の方法を検討してみましょう。したがって、私たちの目標は、LCAを計算することです。 定数時間 ~ O(1) 。どうすればそれを達成できるか見てみましょう。
方法 4 : 範囲最小クエリを使用する
私たちは話し合いました 二分木のLCAとRMQ 。ここでは、n 分木の LCA 問題から RMQ 問題への変換について説明します。
Pre-requisites:- LCA in Binary Tree using RMQ RMQ using sparse table
主要なコンセプト: この方法では、LCA 問題を静的配列上の RMQ (Range Minimum Query) 問題に還元します。それを実行したら、範囲最小クエリを必要な LCA クエリに関連付けます。
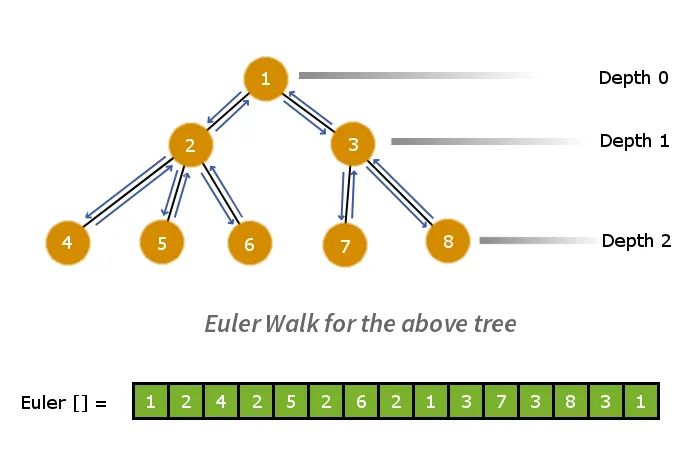
最初のステップは、ツリーをフラットな線形配列に分解することです。これを行うには、オイラー ウォークを適用します。オイラー ウォークにより、グラフの事前順序走査が行われます。したがって、ツリー上でオイラー ウォークを実行し、ノードを訪問するときにノードを配列に保存します。このプロセスによりツリーが縮小されます > 
ここで一般的な観点から考えてみましょう。ツリー上の任意の 2 つのノードを考えてみましょう。両方のノードを接続するパスが 1 つだけ存在し、パス内で最小の深さ値を持つノードが、指定された 2 つのノードの LCA になります。
ここで、任意の 2 つの異なるノードを取り上げます。 で そして v オイラーウォーク配列で。これで、u から v へのパス内のすべての要素が、オイラー ウォーク配列のノード u と v のインデックスの間に位置します。したがって、オイラー配列内のノード u とノード v のインデックス間の最小深さのノードを計算するだけで済みます。
このために、RMQ アルゴリズムを適用できるように、オイラー ウォーク配列内の位置に対応するすべてのノードの深さを含む別の配列を維持します。
以下に、深度トラック配列と平行なオイラー ウォーク配列を示します。

例:- 2 つのノードを考えてみましょう ノード6 そして ノード7 オイラー配列で。ノード 6 とノード 7 の LCA を計算するには、ノード 6 とノード 7 の間のすべてのノードの最小深度値を調べます。
したがって ノード1 最小のものがあります 深度値 = 0 したがって、これはノード 6 とノード 7 の LCA になります。

実装:-
We will be maintaining three arrays 1) Euler Path 2) Depth array 3) First Appearance Index
オイラー パスと深さ配列は上記と同じです
初出インデックス FAI[] : First Appearance インデックス配列には、オイラー パス配列内のすべてのノードの最初の位置のインデックスが格納されます。 FAI[i] = オイラーウォーク配列の i 番目のノードの最初の出現。
上記のメソッドの実装を以下に示します。
実装:
C++ // C++ program to demonstrate LCA of n-ary tree // in constant time. #include 'bits/stdc++.h' using namespace std ; #define sz 101 vector < int > adj [ sz ]; // stores the tree vector < int > euler ; // tracks the eulerwalk vector < int > depthArr ; // depth for each node corresponding // to eulerwalk int FAI [ sz ]; // stores first appearance index of every node int level [ sz ]; // stores depth for all nodes in the tree int ptr ; // pointer to euler walk int dp [ sz ][ 18 ]; // sparse table int logn [ sz ]; // stores log values int p2 [ 20 ]; // stores power of 2 void buildSparseTable ( int n ) { // initializing sparse table memset ( dp -1 sizeof ( dp )); // filling base case values for ( int i = 1 ; i < n ; i ++ ) dp [ i -1 ][ 0 ] = ( depthArr [ i ] > depthArr [ i -1 ]) ? i -1 : i ; // dp to fill sparse table for ( int l = 1 ; l < 15 ; l ++ ) for ( int i = 0 ; i < n ; i ++ ) if ( dp [ i ][ l -1 ] != -1 and dp [ i + p2 [ l -1 ]][ l -1 ] != -1 ) dp [ i ][ l ] = ( depthArr [ dp [ i ][ l -1 ]] > depthArr [ dp [ i + p2 [ l -1 ]][ l -1 ]]) ? dp [ i + p2 [ l -1 ]][ l -1 ] : dp [ i ][ l -1 ]; else break ; } int query ( int l int r ) { int d = r - l ; int dx = logn [ d ]; if ( l == r ) return l ; if ( depthArr [ dp [ l ][ dx ]] > depthArr [ dp [ r - p2 [ dx ]][ dx ]]) return dp [ r - p2 [ dx ]][ dx ]; else return dp [ l ][ dx ]; } void preprocess () { // memorizing powers of 2 p2 [ 0 ] = 1 ; for ( int i = 1 ; i < 18 ; i ++ ) p2 [ i ] = p2 [ i -1 ] * 2 ; // memorizing all log(n) values int val = 1 ptr = 0 ; for ( int i = 1 ; i < sz ; i ++ ) { logn [ i ] = ptr -1 ; if ( val == i ) { val *= 2 ; logn [ i ] = ptr ; ptr ++ ; } } } /** * Euler Walk ( preorder traversal) * converting tree to linear depthArray * Time Complexity : O(n) * */ void dfs ( int cur int prev int dep ) { // marking FAI for cur node if ( FAI [ cur ] == -1 ) FAI [ cur ] = ptr ; level [ cur ] = dep ; // pushing root to euler walk euler . push_back ( cur ); // incrementing euler walk pointer ptr ++ ; for ( auto x : adj [ cur ]) { if ( x != prev ) { dfs ( x cur dep + 1 ); // pushing cur again in backtrack // of euler walk euler . push_back ( cur ); // increment euler walk pointer ptr ++ ; } } } // Create Level depthArray corresponding // to the Euler walk Array void makeArr () { for ( auto x : euler ) depthArr . push_back ( level [ x ]); } int LCA ( int u int v ) { // trivial case if ( u == v ) return u ; if ( FAI [ u ] > FAI [ v ]) swap ( u v ); // doing RMQ in the required range return euler [ query ( FAI [ u ] FAI [ v ])]; } void addEdge ( int u int v ) { adj [ u ]. push_back ( v ); adj [ v ]. push_back ( u ); } int main ( int argc char const * argv []) { // constructing the described tree int numberOfNodes = 8 ; addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 2 4 ); addEdge ( 2 5 ); addEdge ( 2 6 ); addEdge ( 3 7 ); addEdge ( 3 8 ); // performing required precalculations preprocess (); // doing the Euler walk ptr = 0 ; memset ( FAI -1 sizeof ( FAI )); dfs ( 1 0 0 ); // creating depthArray corresponding to euler[] makeArr (); // building sparse table buildSparseTable ( depthArr . size ()); cout < < 'LCA(67) : ' < < LCA ( 6 7 ) < < ' n ' ; cout < < 'LCA(64) : ' < < LCA ( 6 4 ) < < ' n ' ; return 0 ; }
Java // Java program to demonstrate LCA of n-ary // tree in constant time. import java.util.ArrayList ; import java.util.Arrays ; class GFG { static int sz = 101 ; @SuppressWarnings ( 'unchecked' ) // Stores the tree static ArrayList < Integer >[] adj = new ArrayList [ sz ] ; // Tracks the eulerwalk static ArrayList < Integer > euler = new ArrayList <> (); // Depth for each node corresponding static ArrayList < Integer > depthArr = new ArrayList <> (); // to eulerwalk // Stores first appearance index of every node static int [] FAI = new int [ sz ] ; // Stores depth for all nodes in the tree static int [] level = new int [ sz ] ; // Pointer to euler walk static int ptr ; // Sparse table static int [][] dp = new int [ sz ][ 18 ] ; // Stores log values static int [] logn = new int [ sz ] ; // Stores power of 2 static int [] p2 = new int [ 20 ] ; static void buildSparseTable ( int n ) { // Initializing sparse table for ( int i = 0 ; i < sz ; i ++ ) { for ( int j = 0 ; j < 18 ; j ++ ) { dp [ i ][ j ] = - 1 ; } } // Filling base case values for ( int i = 1 ; i < n ; i ++ ) dp [ i - 1 ][ 0 ] = ( depthArr . get ( i ) > depthArr . get ( i - 1 )) ? i - 1 : i ; // dp to fill sparse table for ( int l = 1 ; l < 15 ; l ++ ) for ( int i = 0 ; i < n ; i ++ ) if ( dp [ i ][ l - 1 ] != - 1 && dp [ i + p2 [ l - 1 ]][ l - 1 ] != - 1 ) dp [ i ][ l ] = ( depthArr . get ( dp [ i ][ l - 1 ] ) > depthArr . get ( dp [ i + p2 [ l - 1 ]][ l - 1 ] )) ? dp [ i + p2 [ l - 1 ]][ l - 1 ] : dp [ i ][ l - 1 ] ; else break ; } static int query ( int l int r ) { int d = r - l ; int dx = logn [ d ] ; if ( l == r ) return l ; if ( depthArr . get ( dp [ l ][ dx ] ) > depthArr . get ( dp [ r - p2 [ dx ]][ dx ] )) return dp [ r - p2 [ dx ]][ dx ] ; else return dp [ l ][ dx ] ; } static void preprocess () { // Memorizing powers of 2 p2 [ 0 ] = 1 ; for ( int i = 1 ; i < 18 ; i ++ ) p2 [ i ] = p2 [ i - 1 ] * 2 ; // Memorizing all log(n) values int val = 1 ptr = 0 ; for ( int i = 1 ; i < sz ; i ++ ) { logn [ i ] = ptr - 1 ; if ( val == i ) { val *= 2 ; logn [ i ] = ptr ; ptr ++ ; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs ( int cur int prev int dep ) { // Marking FAI for cur node if ( FAI [ cur ] == - 1 ) FAI [ cur ] = ptr ; level [ cur ] = dep ; // Pushing root to euler walk euler . add ( cur ); // Incrementing euler walk pointer ptr ++ ; for ( Integer x : adj [ cur ] ) { if ( x != prev ) { dfs ( x cur dep + 1 ); // Pushing cur again in backtrack // of euler walk euler . add ( cur ); // Increment euler walk pointer ptr ++ ; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr () { for ( Integer x : euler ) depthArr . add ( level [ x ] ); } static int LCA ( int u int v ) { // Trivial case if ( u == v ) return u ; if ( FAI [ u ] > FAI [ v ] ) { int temp = u ; u = v ; v = temp ; } // Doing RMQ in the required range return euler . get ( query ( FAI [ u ] FAI [ v ] )); } static void addEdge ( int u int v ) { adj [ u ] . add ( v ); adj [ v ] . add ( u ); } // Driver code public static void main ( String [] args ) { for ( int i = 0 ; i < sz ; i ++ ) { adj [ i ] = new ArrayList <> (); } // Constructing the described tree int numberOfNodes = 8 ; addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 2 4 ); addEdge ( 2 5 ); addEdge ( 2 6 ); addEdge ( 3 7 ); addEdge ( 3 8 ); // Performing required precalculations preprocess (); // Doing the Euler walk ptr = 0 ; Arrays . fill ( FAI - 1 ); dfs ( 1 0 0 ); // Creating depthArray corresponding to euler[] makeArr (); // Building sparse table buildSparseTable ( depthArr . size ()); System . out . println ( 'LCA(67) : ' + LCA ( 6 7 )); System . out . println ( 'LCA(64) : ' + LCA ( 6 4 )); } } // This code is contributed by sanjeev2552
Python3 # Python program to demonstrate LCA of n-ary tree # in constant time. from typing import List # stores the tree adj = [[] for _ in range ( 101 )] # tracks the eulerwalk euler = [] # depth for each node corresponding to eulerwalk depthArr = [] # stores first appearance index of every node FAI = [ - 1 ] * 101 # stores depth for all nodes in the tree level = [ 0 ] * 101 # pointer to euler walk ptr = 0 # sparse table dp = [[ - 1 ] * 18 for _ in range ( 101 )] # stores log values logn = [ 0 ] * 101 # stores power of 2 p2 = [ 0 ] * 20 def buildSparseTable ( n : int ): # initializing sparse table for i in range ( n ): dp [ i ][ 0 ] = i - 1 if depthArr [ i ] > depthArr [ i - 1 ] else i # dp to fill sparse table for l in range ( 1 15 ): for i in range ( n ): if dp [ i ][ l - 1 ] != - 1 and dp [ i + p2 [ l - 1 ]][ l - 1 ] != - 1 : dp [ i ][ l ] = dp [ i + p2 [ l - 1 ]][ l - 1 ] if depthArr [ dp [ i ][ l - 1 ] ] > depthArr [ dp [ i + p2 [ l - 1 ]][ l - 1 ]] else dp [ i ][ l - 1 ] else : break def query ( l : int r : int ) -> int : d = r - l dx = logn [ d ] if l == r : return l if depthArr [ dp [ l ][ dx ]] > depthArr [ dp [ r - p2 [ dx ]][ dx ]]: return dp [ r - p2 [ dx ]][ dx ] else : return dp [ l ][ dx ] def preprocess (): global ptr # memorizing powers of 2 p2 [ 0 ] = 1 for i in range ( 1 18 ): p2 [ i ] = p2 [ i - 1 ] * 2 # memorizing all log(n) values val = 1 ptr = 0 for i in range ( 1 101 ): logn [ i ] = ptr - 1 if val == i : val *= 2 logn [ i ] = ptr ptr += 1 def dfs ( cur : int prev : int dep : int ): global ptr # marking FAI for cur node if FAI [ cur ] == - 1 : FAI [ cur ] = ptr level [ cur ] = dep # pushing root to euler walk euler . append ( cur ) # incrementing euler walk pointer ptr += 1 for x in adj [ cur ]: if x != prev : dfs ( x cur dep + 1 ) # pushing cur again in backtrack # of euler walk euler . append ( cur ) # increment euler walk pointer ptr += 1 # Create Level depthArray corresponding # to the Euler walk Array def makeArr (): global depthArr for x in euler : depthArr . append ( level [ x ]) def LCA ( u : int v : int ) -> int : # trivial case if u == v : return u if FAI [ u ] > FAI [ v ]: u v = v u # doing RMQ in the required range return euler [ query ( FAI [ u ] FAI [ v ])] def addEdge ( u v ): adj [ u ] . append ( v ) adj [ v ] . append ( u ) # constructing the described tree numberOfNodes = 8 addEdge ( 1 2 ) addEdge ( 1 3 ) addEdge ( 2 4 ) addEdge ( 2 5 ) addEdge ( 2 6 ) addEdge ( 3 7 ) addEdge ( 3 8 ) # performing required precalculations preprocess () # doing the Euler walk ptr = 0 FAI = [ - 1 ] * ( numberOfNodes + 1 ) dfs ( 1 0 0 ) # creating depthArray corresponding to euler[] makeArr () # building sparse table buildSparseTable ( len ( depthArr )) print ( 'LCA(67) : ' LCA ( 6 7 )) print ( 'LCA(64) : ' LCA ( 6 4 ))
C# // C# program to demonstrate LCA of n-ary // tree in constant time. using System ; using System.Collections.Generic ; public class GFG { static int sz = 101 ; // Stores the tree static List < int > [] adj = new List < int > [ sz ]; // Tracks the eulerwalk static List < int > euler = new List < int > (); // Depth for each node corresponding static List < int > depthArr = new List < int > (); // to eulerwalk // Stores first appearance index of every node static int [] FAI = new int [ sz ]; // Stores depth for all nodes in the tree static int [] level = new int [ sz ]; // Pointer to euler walk static int ptr ; // Sparse table static int [] dp = new int [ sz 18 ]; // Stores log values static int [] logn = new int [ sz ]; // Stores power of 2 static int [] p2 = new int [ 20 ]; static void buildSparseTable ( int n ) { // Initializing sparse table for ( int i = 0 ; i < sz ; i ++ ) { for ( int j = 0 ; j < 18 ; j ++ ) { dp [ i j ] = - 1 ; } } // Filling base case values for ( int i = 1 ; i < n ; i ++ ) dp [ i - 1 0 ] = ( depthArr [ i ] > depthArr [ i - 1 ]) ? i - 1 : i ; // dp to fill sparse table for ( int l = 1 ; l < 15 ; l ++ ) for ( int i = 0 ; i < n ; i ++ ) if ( dp [ i l - 1 ] != - 1 && dp [ i + p2 [ l - 1 ] l - 1 ] != - 1 ) dp [ i l ] = ( depthArr [ dp [ i l - 1 ]] > depthArr [ dp [ i + p2 [ l - 1 ] l - 1 ]]) ? dp [ i + p2 [ l - 1 ] l - 1 ] : dp [ i l - 1 ]; else break ; } static int query ( int l int r ) { int d = r - l ; int dx = logn [ d ]; if ( l == r ) return l ; if ( depthArr [ dp [ l dx ]] > depthArr [ dp [ r - p2 [ dx ] dx ]]) return dp [ r - p2 [ dx ] dx ]; else return dp [ l dx ]; } static void preprocess () { // Memorizing powers of 2 p2 [ 0 ] = 1 ; for ( int i = 1 ; i < 18 ; i ++ ) p2 [ i ] = p2 [ i - 1 ] * 2 ; // Memorizing all log(n) values int val = 1 ptr = 0 ; for ( int i = 1 ; i < sz ; i ++ ) { logn [ i ] = ptr - 1 ; if ( val == i ) { val *= 2 ; logn [ i ] = ptr ; ptr ++ ; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs ( int cur int prev int dep ) { // Marking FAI for cur node if ( FAI [ cur ] == - 1 ) FAI [ cur ] = ptr ; level [ cur ] = dep ; // Pushing root to euler walk euler . Add ( cur ); // Incrementing euler walk pointer ptr ++ ; foreach ( int x in adj [ cur ]) { if ( x != prev ) { dfs ( x cur dep + 1 ); euler . Add ( cur ); ptr ++ ; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr () { foreach ( int x in euler ) depthArr . Add ( level [ x ]); } static int LCA ( int u int v ) { // Trivial case if ( u == v ) return u ; if ( FAI [ u ] > FAI [ v ]) { int temp = u ; u = v ; v = temp ; } // Doing RMQ in the required range return euler [ query ( FAI [ u ] FAI [ v ])]; } static void addEdge ( int u int v ) { adj [ u ]. Add ( v ); adj [ v ]. Add ( u ); } // Driver Code static void Main ( string [] args ) { int sz = 9 ; adj = new List < int > [ sz ]; for ( int i = 0 ; i < sz ; i ++ ) { adj [ i ] = new List < int > (); } // Constructing the described tree int numberOfNodes = 8 ; addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 2 4 ); addEdge ( 2 5 ); addEdge ( 2 6 ); addEdge ( 3 7 ); addEdge ( 3 8 ); // Performing required precalculations preprocess (); // Doing the Euler walk ptr = 0 ; Array . Fill ( FAI - 1 ); dfs ( 1 0 0 ); // Creating depthArray corresponding to euler[] makeArr (); // Building sparse table buildSparseTable ( depthArr . Count ); Console . WriteLine ( 'LCA(67) : ' + LCA ( 6 7 )); Console . WriteLine ( 'LCA(64) : ' + LCA ( 6 4 )); } } // This code is contributed by Prince Kumar
JavaScript let adj = []; for ( let _ = 0 ; _ < 101 ; _ ++ ) { adj . push ([]); } // tracks the eulerwalk let euler = []; // depth for each node corresponding to eulerwalk let depthArr = []; // stores first appearance index of every node let FAI = new Array ( 101 ). fill ( - 1 ); // stores depth for all nodes in the tree let level = new Array ( 101 ). fill ( 0 ); // pointer to euler walk let ptr = 0 ; // sparse table let dp = []; for ( let _ = 0 ; _ < 101 ; _ ++ ) { dp . push ( new Array ( 18 ). fill ( - 1 )); } // stores log values let logn = new Array ( 101 ). fill ( 0 ); // stores power of 2 let p2 = new Array ( 20 ). fill ( 0 ); function buildSparseTable ( n ) { // initializing sparse table for ( let i = 0 ; i < n ; i ++ ) { dp [ i ][ 0 ] = i - 1 >= 0 && depthArr [ i ] > depthArr [ i - 1 ] ? i - 1 : i ; } // dp to fill sparse table for ( let l = 1 ; l < 15 ; l ++ ) { for ( let i = 0 ; i < n ; i ++ ) { if ( dp [ i ][ l - 1 ] !== - 1 && dp [ i + p2 [ l - 1 ]][ l - 1 ] !== - 1 ) { dp [ i ][ l ] = depthArr [ dp [ i ][ l - 1 ]] > depthArr [ dp [ i + p2 [ l - 1 ]][ l - 1 ]] ? dp [ i + p2 [ l - 1 ]][ l - 1 ] : dp [ i ][ l - 1 ]; } else { break ; } } } } function query ( l r ) { let d = r - l ; let dx = logn [ d ]; if ( l === r ) { return l ; } if ( depthArr [ dp [ l ][ dx ]] > depthArr [ dp [ r - p2 [ dx ]][ dx ]]) { return dp [ r - p2 [ dx ]][ dx ]; } else { return dp [ l ][ dx ]; } } function preprocess () { // memorizing powers of 2 p2 [ 0 ] = 1 ; for ( let i = 1 ; i < 18 ; i ++ ) { p2 [ i ] = p2 [ i - 1 ] * 2 ; } // memorizing all log(n) values let val = 1 ; ptr = 0 ; for ( let i = 1 ; i < 101 ; i ++ ) { logn [ i ] = ptr - 1 ; if ( val === i ) { val *= 2 ; logn [ i ] = ptr ; ptr += 1 ; } } } function dfs ( cur prev dep ) { // marking FAI for cur node if ( FAI [ cur ] === - 1 ) { FAI [ cur ] = ptr ; } level [ cur ] = dep ; // pushing root to euler walk euler . push ( cur ); // incrementing euler walk pointer ptr += 1 ; for ( let x of adj [ cur ]) { if ( x !== prev ) { dfs ( x cur dep + 1 ); // pushing cur again in backtrack // of euler walk euler . push ( cur ); // increment euler walk pointer ptr += 1 ; } } } // Create Level depthArray corresponding // to the Euler walk Array function makeArr () { for ( let x of euler ) { depthArr . push ( level [ x ]); } } function LCA ( u v ) { // trivial case if ( u === v ) { return u ; } if ( FAI [ u ] > FAI [ v ]) { [ u v ] = [ v u ]; } // doing RMQ in the required range return euler [ query ( FAI [ u ] FAI [ v ])]; } function addEdge ( u v ) { adj [ u ]. push ( v ); adj [ v ]. push ( u ); } // constructing the described tree let numberOfNodes = 8 ; addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 2 4 ); addEdge ( 2 5 ); addEdge ( 2 6 ); addEdge ( 3 7 ); addEdge ( 3 8 ); // performing required precalculations preprocess (); // doing the Euler walk ptr = 0 ; FAI = new Array ( numberOfNodes + 1 ). fill ( - 1 ); dfs ( 1 0 0 ); // creating depthArray corresponding to euler[] makeArr (); // building sparse table buildSparseTable ( depthArr . length ); console . log ( 'LCA(67) : ' LCA ( 6 7 )); console . log ( 'LCA(64) : ' LCA ( 6 4 ));
出力
LCA(67) : 1 LCA(64) : 2
注記 : クエリごとの時間の複雑さを一定にするために、必要な 2 の累乗をすべて事前計算し、必要なログ値もすべて事前計算しています。そうでなければ、すべてのクエリ操作に対してログ計算を行った場合、時間計算量は一定ではなくなります。
時間計算量: LCA から RMQ への変換プロセスは、オイラー ウォークによって実行されます。 の上) 時間。
RMQ のスパース テーブルの前処理には O(nlogn) 時間がかかり、各クエリへの応答は一定時間のプロセスです。したがって、全体的な時間計算量は O(nlogn) - 前処理と ○(1) クエリごとに。
補助スペース: O(n+s)
クイズの作成