Programmazione lineare
Programmazione lineare è un concetto matematico che viene utilizzato per trovare la soluzione ottima della funzione lineare. Questo metodo utilizza semplici presupposti per ottimizzare la funzione data. La programmazione lineare ha un'enorme applicazione nel mondo reale e viene utilizzata per risolvere vari tipi di problemi.
La programmazione lineare viene utilizzata in vari settori come l'industria marittima, l'industria manifatturiera, l'industria dei trasporti, le telecomunicazioni e altri.
Il termine programmazione lineare è composto da due parole lineare e programmazione, la parola lineare indica la relazione tra vari tipi di variabili di primo grado utilizzate in un problema e la parola programmazione ci indica la procedura passo passo per risolvere questi problemi.
In questo articolo impareremo in dettaglio la programmazione lineare, i suoi esempi, le formule e altri concetti.
Tabella dei contenuti
- Cos'è la programmazione lineare?
- Componenti della Programmazione Lineare
- Esempi di programmazione lineare
- Problemi di programmazione lineare
- Tipi di problemi di programmazione lineare
- Formula di programmazione lineare
- Come risolvere i problemi di programmazione lineare?
- Metodi di programmazione lineare
- Metodo del simplesso di programmazione lineare
- Metodo grafico di programmazione lineare
- Applicazioni di programmazione lineare
- Importanza della programmazione lineare
- Applicazioni aggiornate della programmazione lineare
- Programmazione lineare nella ricerca operativa
- Metodo del semplice
Cos'è la programmazione lineare?
Programmazione lineare O Ottimizzazione lineare è una tecnica che ci aiuta a trovare la soluzione ottimale per un dato problema, una soluzione ottimale è una soluzione che rappresenta il miglior risultato possibile di un dato problema particolare.
In parole povere è il metodo per scoprire come fare qualcosa nel miglior modo possibile. Con risorse limitate, è necessario utilizzare in modo ottimale le risorse e ottenere il miglior risultato possibile in un obiettivo particolare, ad esempio il minor costo, il margine più elevato o il minor tempo.
La situazione che richiede la ricerca dei migliori valori delle variabili soggette a determinati vincoli è quella in cui utilizziamo problemi di programmazione lineare. Queste situazioni non possono essere gestite con i consueti calcoli e tecniche numeriche.
Definizione di programmazione lineare
La programmazione lineare è la tecnica utilizzata per ottimizzare un particolare scenario. L'uso della programmazione lineare ci fornisce il miglior risultato possibile in una determinata situazione. Utilizza tutte le risorse disponibili in modo tale da produrre il risultato ottimale.
Componenti della Programmazione Lineare
I componenti di base di un problema di programmazione lineare (LP) sono:
- Variabili decisionali: Variabili che si desidera determinare per ottenere la soluzione ottimale.
- Funzione obiettivo: M equazione atematica che rappresenta l'obiettivo che si desidera raggiungere
- Vincoli: Limitazioni o restrizioni che le variabili decisionali devono seguire.
- Restrizioni di non negatività: In qualche scenari del mondo reale, le variabili decisionali non possono essere negative
Ulteriori caratteristiche della programmazione lineare
- Finitezza: Il numero di variabili decisionali e di vincoli in un problema di LP è finito.
- Linearità: La funzione obiettivo e tutti i vincoli devono essere funzioni lineari delle variabili decisionali . Ciò significa che il grado delle variabili dovrebbe essere uno.
Esempi di programmazione lineare
Possiamo comprendere le situazioni in cui viene applicata la programmazione lineare con l'aiuto dell'esempio discusso di seguito,
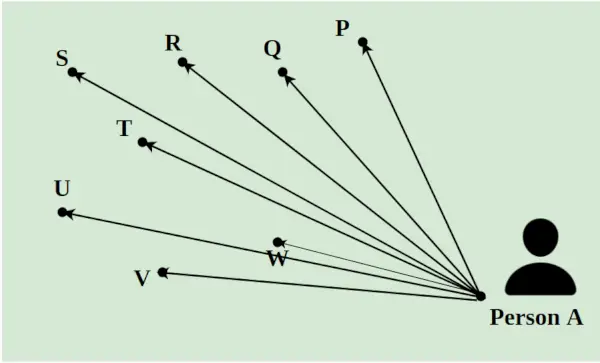
Supponiamo che un fattorino debba consegnare 8 pacchi in un giorno in diverse località di una città. Deve prendere tutti i pacchetti da A e consegnarli ai punti P, Q, R, S, T, U, V e W. La distanza tra loro è indicata utilizzando le linee come mostrato nell'immagine qui sotto. Il percorso più breve seguito dal fattorino viene calcolato utilizzando il concetto di programmazione lineare.

Problemi di programmazione lineare
Problemi di programmazione lineare (LPP) comportano l'ottimizzazione di una funzione lineare per trovare la soluzione di valore ottimale per la funzione. Il valore ottimale può essere il valore massimo o il valore minimo.
In LPP vengono chiamate le funzioni lineari funzioni oggettive. Una funzione obiettivo può avere più variabili, che sono soggette a condizioni e devono soddisfarle vincoli lineari .
Tipi di problemi di programmazione lineare
Esistono molti diversi problemi di programmazione lineare (LPP), ma in questo articolo affronteremo tre principali problemi di programmazione lineare.
Problemi di produzione
I problemi di produzione riguardano il numero di unità che dovrebbero essere prodotte o vendute per massimizzare i profitti quando ciascun prodotto richiede manodopera, ore macchina e materie prime fisse.
Problemi di dieta
Viene utilizzato per calcolare il numero di diversi tipi di componenti da includere nella dieta per ottenere il costo minimo, in base alla disponibilità degli alimenti e ai relativi prezzi.
Problemi di trasporto
Viene utilizzato per determinare il programma di trasporto per trovare il modo più economico di trasportare un prodotto da stabilimenti/fabbriche situati in luoghi diversi a mercati diversi.
Formula di programmazione lineare
Un problema di programmazione lineare consiste in:
- Variabili decisionali
- Funzione obiettivo
- Vincoli
- Restrizioni non negative
Variabili decisionali sono le variabili x e y, che decidono l'output del problema di programmazione lineare e rappresentano la soluzione finale.
IL funzione obiettivo , generalmente rappresentata da Z, è la funzione lineare che deve essere ottimizzata in base alla condizione data per ottenere la soluzione finale.
IL restrizioni imposti alle variabili decisionali che ne limitano i valori sono chiamati vincoli.
Ora, la formula generale di un problema di programmazione lineare è:
Funzione obiettivo : Z = ascia + da
Vincoli: cx + dy ≥ e, px + qy ≤ r
Restrizioni non negative: x ≥ 0, y ≥ 0
Nella condizione precedente x e y sono le variabili decisionali.
Come risolvere i problemi di programmazione lineare?
Prima di risolvere i problemi di programmazione lineare dobbiamo formulare i problemi secondo i parametri standard. I passaggi per risolvere i problemi di programmazione lineare sono:
Passo 1: Segna le variabili decisionali nel problema.
Passo 2: Costruisci la funzione obiettivo del problema e controlla se la funzione deve essere minimizzata o massimizzata.
Passaggio 3: Annotare tutti i vincoli dei problemi lineari.
Passaggio 4: Garantire restrizioni non negative delle variabili decisionali.
Passaggio 5: Ora risolvi il problema della programmazione lineare utilizzando qualsiasi metodo, generalmente utilizziamo il metodo del simplesso o quello grafico.
Metodi di programmazione lineare
Utilizziamo vari metodi per risolvere problemi di programmazione lineare. I due metodi più comuni utilizzati sono:
- Metodo del semplice
- Metodo grafico
Impariamo questi due metodi in dettaglio in questo articolo,
Metodo del simplesso di programmazione lineare
Uno dei metodi più comuni per risolvere il problema della programmazione lineare è il metodo del simplesso. In questo metodo, ripetiamo una condizione specifica “n” un numero di volte fino a ottenere una soluzione ottimale.
I passaggi necessari per risolvere problemi di programmazione lineare utilizzando il metodo del simplesso sono:
Passo 1: Formulare i problemi di programmazione lineare in base ai vincoli dati.
Passo 2: Converti tutte le disuguaglianze date in equazioni o uguaglianze dei problemi di programmazione lineare aggiungendo la variabile slack a ciascuna disuguaglianza, ove richiesto.
Passaggio 3: Costruisci la tabella simplex iniziale. Rappresentando ciascuna equazione di vincolo in una riga e scrivendo la funzione obiettivo nella riga inferiore. La tabella così ottenuta prende il nome di tabella del Simplesso.
Passaggio 4: Identifica la voce negativa più grande nella riga inferiore, la colonna dell'elemento con la voce negativa più alta è chiamata colonna pivot
Passaggio 5: Dividere le voci della colonna più a destra con le voci della rispettiva colonna pivot, escluse le voci della riga più in basso. Ora la riga contenente il minor numero di voci è chiamata riga pivot. L'elemento pivot è ottenuto dall'intersezione della riga pivot e della colonna pivot.
Passaggio 6: Utilizzando l'operazione matrice e con l'aiuto dell'elemento pivot, tutte le voci nella colonna pivot devono essere pari a zero.
Passaggio 7: Controlla le voci non negative nella riga più in basso. Se non ci sono voci negative nella riga inferiore, termina il processo altrimenti avvia nuovamente il processo dal passaggio 4.
Passaggio 8: La tabella finale del simplesso così ottenuta fornisce la soluzione al nostro problema.
Metodo grafico di programmazione lineare
Il metodo grafico è un metodo diverso dal metodo Simplex che viene utilizzato per risolvere problemi di programmazione lineare. Come suggerisce il nome, questo metodo utilizza i grafici per risolvere i problemi di programmazione lineare indicati. Questo è il metodo migliore per risolvere problemi di programmazione lineare e richiede meno sforzo rispetto al metodo del simplesso.
Utilizzando questo metodo tracciamo tutte le disuguaglianze soggette a vincoli nei problemi di programmazione lineare dati. Non appena tutte le disuguaglianze del dato LPP vengono tracciate nel grafico XY, la regione comune di tutte le disuguaglianze fornisce la soluzione ottima. Vengono calcolati tutti i punti d'angolo della regione ammissibile e viene calcolato il valore della funzione obiettivo in tutti quei punti, quindi confrontando questi valori si ottiene la soluzione ottima dell'LPP.
Esempio: trovare il valore massimo e minimo di z = 6x + 9y quando le condizioni di vincolo sono,
- 2x + 3y ≤ 12
- x e y ≥ 0
- x + y ≤ 5
Soluzione:
Passo 1 : Per prima cosa converti le disequazioni in equazioni normali. Quindi le equazioni saranno 2x+3y = 0, x = 0, y = 0 e x + y = 5.
Passo 2 : Trova i punti in cui 2x + 3y e x + y = 5 tagliano l'asse x e l'asse y. Per trovare il punto di intersezione dell'asse x inserisci y = 0 nella rispettiva equazione e trova il punto. Allo stesso modo per i punti di intersezione dell'asse y inserire x = 0 nella rispettiva equazione.
Passaggio 3 : traccia le due linee che tagliano l'asse x e l'asse y. Troviamo che i due assi si tagliano a vicenda in (3,2).
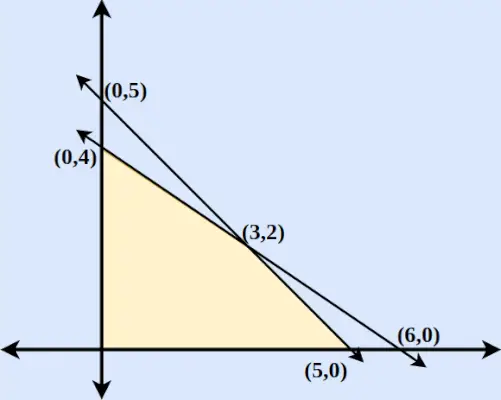
Passaggio 4 : Per x ≥ 0 ey ≥ 0, troviamo che entrambe le disequazioni sono seguite. Quindi la regione includerà un'area racchiusa da due assi ed entrambe le linee includeranno l'origine. La regione tracciata è mostrata sotto nella figura.
Passaggio 5 : Trova Z per ogni punto e massimi e minimi.
Coordinate Z = 6x + 9y (0,5) Z = 45 (0,4) Z = 36 (5.0) Z = 30 (6.0) Z = 36 (3.2) Z = 36 Quindi, troviamo che Z = 6x + 9y è massimo in (0,5) e minimo in (5,0).
Applicazioni di programmazione lineare
La programmazione lineare ha applicazioni in vari campi. Viene utilizzato per trovare il costo minimo di un processo quando sono dati tutti i vincoli del problema. Viene utilizzato per ottimizzare il costo di trasporto del veicolo, ecc. Varie applicazioni della programmazione lineare sono
Industrie ingegneristiche
Le industrie ingegneristiche utilizzano la programmazione lineare per risolvere problemi di progettazione e produzione e per ottenere il massimo rendimento da una determinata condizione.
Industrie manufatturiere
Le industrie manifatturiere utilizzano la programmazione lineare per massimizzare il profitto delle aziende e ridurre i costi di produzione.
Industrie energetiche
Le aziende energetiche utilizzano la programmazione lineare per ottimizzare la produzione.
Industrie dei trasporti
La programmazione lineare viene utilizzata anche nelle industrie dei trasporti per trovare il percorso per ridurre al minimo i costi di trasporto.
Importanza della programmazione lineare
La programmazione lineare ha un'enorme importanza in vari settori: massimizza il valore di output minimizzando i valori di input in base a vari vincoli.
LP è altamente applicabile quando abbiamo più condizioni durante la risoluzione di un problema e dobbiamo ottimizzare l'output del problema, ovvero dobbiamo trovare il valore minimo o massimo in base a una determinata condizione.
Per saperne di più,
- Disuguaglianze lineari
- Soluzione algebrica di disuguaglianze lineari
Problemi di programmazione lineare
Problema 1: Un'azienda produce e vende due tipi di prodotti e il costo di produzione di ciascuna unità a e b è rispettivamente di 200 e 150 rupie; ciascuna unità di prodotto produce un profitto di 20 rupie e ciascuna unità di prodotto b produce un profitto di 15 rupie sulla vendita . L'azienda stima che la domanda mensile di A e B sia al massimo pari all'unità raccolta in tutto il budget di produzione per il mese fissato a 50.000 rupie. Quante unità dovrebbe produrre l'azienda per ottenere il massimo profitto dalle vendite mensili da un e B?
Soluzione:
Sia x = numero di unità di tipo A
y = Numero di unità di tipo B
Massimizza Z = 40x + 50y
Soggetto ai vincoli
3x + y ≤ 9
x + 2y ≤ 8
e x, y ≥ 0
Considera l'equazione,
3x + y = 9
x = 3
y = 0
e x + 2y = 8
x = 8
y = 0
Ora possiamo determinare il valore massimo di Z valutando il valore di Z nei quattro punti (vertici) mostrati di seguito
Vertici
Z = 40x + 50y
(0, 0)
Z = 40 × 0 + 50 × 0 = Rs. 0
(3, 0)
Z = 40 × 3 + 50 × 0 = Rs. 120
(0, 4)
Z = 40 × 0 + 50 × 4 = Rs. 200
(23)
Z = 40 × 2 + 50 × 3 = Rs. 230
Profitto massimo, Z = Rs. 230
∴ Il numero di unità di tipo A è 2 e il numero di unità di tipo B è 3.
Problema 2: Massimizzare Z = 3x + 4y.
Soggetto a vincoli , x + y ≤ 450, 2x + y ≤ 600 e x, y ≤ 0.
Soluzione:
Abbiamo dal dato
Vincoli (1)
X + Y = 450
Mettendo x = 0, ⇒ 0 + y = 450 ⇒ y = 450
Mettendo y = 0, ⇒ x + 0 = 450 ⇒ x = 450
Da, Vincoli (2)
2x + y = 600
Mettendo x = 0, ⇒ 0 + y = 600 ⇒ y = 600
Mettendo y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300
Ora abbiamo le coordinate dei punti Z = 3x + 4y
| Vertici | Z = 3x + 4y |
|---|---|
| (0, 0) | Z = 3 × 0 + 4 × 0 = 0 |
| (300, 0) | Z = 3 × 300+ 4 × 0 = 900 |
| (150, 300) | Z = 3 × 150 + 4 × 300 = 1650 |
| (0, 450) | Z = 3 × 0 + 4 × 450 = 1800 |
Pertanto, la soluzione ottima massima Z = 1800 alle coordinate x = 0 ey = 450. Il grafico è riportato di seguito.

Applicazioni aggiornate della programmazione lineare
La programmazione lineare, una potente tecnica matematica, viene utilizzata per risolvere problemi di ottimizzazione in vari settori. Ecco alcune applicazioni moderne:
- Ottimizzazione della catena di fornitura : La programmazione lineare aiuta le aziende a ridurre al minimo i costi e a massimizzare l’efficienza nelle loro catene di fornitura. Viene utilizzato per determinare i percorsi di trasporto, le operazioni di magazzino e le strategie di gestione dell'inventario più convenienti.
- Gestione dell'energia : Nel settore energetico, la programmazione lineare viene utilizzata per ottimizzare il mix di metodi di produzione energetica. Ciò include il bilanciamento delle fonti energetiche tradizionali con quelle rinnovabili per ridurre i costi e l’impatto ambientale soddisfacendo al tempo stesso la domanda.
- Progettazione di reti di telecomunicazioni : La programmazione lineare aiuta nella progettazione di reti di telecomunicazioni efficienti. Aiuta ad allocare la larghezza di banda, progettare layout di rete e ottimizzare il flusso di dati per garantire comunicazioni ad alta velocità a costi inferiori.
- Progetto finanziario : Le aziende e gli analisti finanziari utilizzano la programmazione lineare per l'ottimizzazione del portafoglio, la gestione del rischio e il budget di capitale. Aiuta a prendere decisioni di investimento che massimizzano i rendimenti minimizzando il rischio.
- Logistica Sanitaria : Nel settore sanitario, la programmazione lineare viene applicata per ottimizzare l'allocazione delle risorse, come letti ospedalieri, personale medico e attrezzature. È fondamentale per migliorare l’assistenza ai pazienti, ridurre i tempi di attesa e gestire i costi in modo efficace.
- Ottimizzazione del processo di produzione : La programmazione lineare viene utilizzata per determinare i livelli di produzione ottimali per più prodotti all'interno di un impianto di produzione, considerando vincoli quali manodopera, materiali e disponibilità delle macchine.
- Pianificazione agricola : Gli agricoltori e i pianificatori agricoli utilizzano la programmazione lineare per decidere sulla selezione delle colture, sull’uso del terreno e sull’allocazione delle risorse per massimizzare rendimenti e profitti preservando le risorse.
- Pianificazione dell'equipaggio della compagnia aerea : Le compagnie aeree utilizzano la programmazione lineare per programmare gli equipaggi in modo efficiente, garantendo che il personale dei voli sia conforme alle normative e riducendo al minimo i costi operativi.
Queste applicazioni dimostrano la versatilità e la potenza della programmazione lineare nel risolvere complessi problemi di ottimizzazione in vari settori, dimostrandone la rilevanza nel mondo odierno basato sui dati.
Programmazione lineare nella ricerca operativa
- Strumento fondamentale : La programmazione lineare è uno strumento fondamentale nella ricerca operativa per l'ottimizzazione delle risorse.
- Il processo decisionale : Aiuta a prendere le decisioni migliori riguardo all'allocazione delle risorse, alla massimizzazione dei profitti o alla minimizzazione dei costi.
- Ampie applicazioni : Utilizzato in vari campi come la logistica, la produzione, la finanza e la sanità per risolvere problemi complessi.
- Modellazione di problemi del mondo reale : Trasforma i problemi del mondo reale in modelli matematici per trovare le soluzioni più efficienti.
Metodo del semplice
- Algoritmo di ottimizzazione : Il metodo del simplesso è un potente algoritmo utilizzato nella programmazione lineare per trovare la soluzione ottima alle disuguaglianze lineari.
- Approccio graduale : Si muove iterativamente verso la soluzione migliore navigando lungo i bordi della regione ammissibile definita da vincoli.
- Efficienza : Noto per la sua efficienza nel risolvere problemi di programmazione lineare su larga scala.
- Versatilità : Applicabile in vari ambiti come la pianificazione della dieta, i flussi di rete, la pianificazione della produzione e altro ancora, dimostrando la sua versatilità.
Programmazione lineare – Domande frequenti
Cos'è la programmazione lineare?
La programmazione lineare è un concetto matematico utilizzato per ottimizzare un dato problema lineare che presenta una varietà di vincoli. Usando la programmazione lineare otteniamo il risultato ottimale del problema dato
Cosa sono i problemi di programmazione lineare?
I problemi di programmazione lineare (LPP) sono i problemi che forniscono la soluzione ottima alle condizioni date.
Cos'è la formula di programmazione lineare?
Le formule di programmazione lineare generale sono,
- Funzione Obiettivo: Z = ax + by
- Vincoli: px + qy ≤ r, sx + ty ≤ u
- Restrizioni non negative: x ≥ 0, y ≥ 0
Quali sono i diversi tipi di programmazione lineare?
Diversi tipi di metodi di programmazione lineare sono,
- Programmazione lineare con il metodo del simplesso
- Programmazione lineare con il metodo R
- Programmazione lineare con metodo grafico
Quali sono i requisiti della programmazione lineare?
Vari requisiti dei problemi di programmazione lineare sono:
- Linearità
- Funzione obiettivo
- Vincoli
- Non negatività
Quali sono i vantaggi della Programmazione Lineare?
Vari vantaggi della programmazione lineare sono:
- Fornisce la soluzione ottimale a qualsiasi problema lineare.
- È facile da usare e dà sempre risultati coerenti
- Aiuta a massimizzare i profitti e a ridurre i costi di produzione.