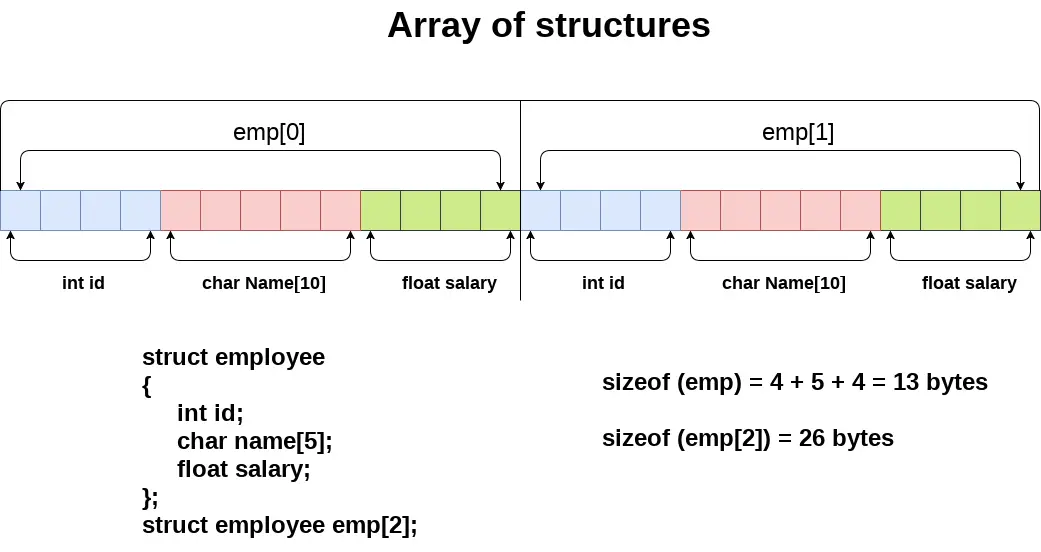
IDENTITÀ TRIGONOMETRICHE INVERSE

Identità trigonometriche inverse: In matematica, le funzioni trigonometriche inverse sono note anche come funzioni arcus o funzioni antitrigonometriche. Le funzioni trigonometriche inverse sono le funzioni inverse delle funzioni trigonometriche di base, ovvero seno, coseno, tangente, cosecante, secante e cotangente. Si usa per trovare gli angoli con qualsiasi rapporto trigonometrico. Le funzioni trigonometriche inverse sono generalmente utilizzate in campi come geometria, ingegneria, ecc. La rappresentazione delle funzioni trigonometriche inverse sono:

Se a = f(b), allora la funzione inversa lo è

b = f ^-1 (UN)

Esempi di funzioni trigonometriche inverse inverse sono sin ^-1 x, cos ^-1 x, quindi ^-1 x, ecc.

Tabella dei contenuti

Dominio e intervallo delle identità trigonometriche inverse
Proprietà delle funzioni trigonometriche inverse
Identità della funzione trigonometrica inversa
Esempi di problemi sulle identità trigonometriche inverse
Problemi pratici sulle identità trigonometriche inverse

Dominio e intervallo delle identità trigonometriche inverse

La tabella seguente mostra alcune funzioni trigonometriche con il loro dominio e intervallo.

Funzione	Dominio	Allineare
y = senza ^-1 X	[-undici]	[-p/2, p/2]
y = cos ^-1 X	[-undici]	[0, p]
y = cosec ^-1 X	R – (-1,1)	[-π/2,π/2] – {0}
y = sec ^-1 X	R - (-undici)	[0, π] – {π/2}
y = così ^-1 X	R	(-p/2, p/2)
y = lettino ^-1 X	R	(0, p)

Proprietà delle funzioni trigonometriche inverse

Le seguenti sono le proprietà delle funzioni trigonometriche inverse:

Proprietà 1:

senza ^-1 (1/x) = cosec ^-1 x, per x ≥ 1 o x ≤ -1
cos ^-1 (1/x) = sec ^-1 x, per x ≥ 1 o x ≤ -1
COSÌ ^-1 (1/x) = lettino ^-1 x, per x> 0

Proprietà 2:

senza ^-1 (-x) = -peccato ^-1 x, per x ∈ [-1 , 1]
COSÌ ^-1 (-x) = -tan ^-1 x, per x ∈ R
cosec ^-1 (-x) = -cosec ^-1 x, per |x| ≥ 1

Proprietà 3

cos ^-1 (-x) = π – cos ^-1 x, per x ∈ [-1 , 1]
sez ^-1 (-x) = π – sec ^-1 x, per |x| ≥ 1
culla ^-1 (-x) = π – lettino ^-1 x, per x ∈ R

Proprietà 4

senza ^-1 x + cos ^-1 x = π/2, per x ∈ [-1,1]
COSÌ ^-1 x + lettino ^-1 x = π/2, per x ∈ R
cosec ^-1 x + sec ^-1 x = π/2 , per |x| ≥ 1

Proprietà 5

COSÌ ^-1 x + così ^-1 y = così ^-1 ( x + y )/(1 – xy), per xy <1
COSÌ ^-1 x – quindi ^-1 y = così ^-1 (x – y)/(1 + xy), per xy> -1
COSÌ ^-1 x + così ^-1 y = π + tan ^-1 (x + y)/(1 – xy), per xy>1 ; x, y>0

Proprietà 6

2tan ^-1 x = peccato ^-1 (2x)/(1+x ² ), per |x| ≤ 1
2tan ^-1 x = cos ^-1 (1-x ² )/(1+x ² ), per x ≥ 0
2tan ^-1 x = così ^-1 (2x)/(1 –x ² ), per -1

Identità della funzione trigonometrica inversa

Le seguenti sono le identità delle funzioni trigonometriche inverse:

senza ^-1 (sin x) = x purché -π/2 ≤ x ≤ π/2
cos ^-1 (cos x) = x purché 0 ≤ x ≤ π
COSÌ ^-1 (tan x) = x purché -π/2
senza ^-1 x) = x purché -1 ≤ x ≤ 1
cos(cos ^-1 x) = x purché -1 ≤ x ≤ 1
così così ^-1 x) = x purché x ∈ R
cosec(cosec ^-1 x) = x purché -1 ≤ x ≤ ∞ o -∞
sec(sec ^-1 x) = x purché 1 ≤ x ≤ ∞ o -∞
lettino(lettino ^-1 x) = x purché -∞
sin^{-1}(frac{2x}{1 + x^2}) = 2 tan^{-1}x
cos^{-1}(frac{1 – x^2}{1 + x^2}) = 2 tan^{-1}x
tan^{-1}(frac{2x}{1 – x^2}) = 2 tan^{-1}x
2cos ^-1 x = cos ^-1 (2x ² - 1)
2peccato ^-1 x = peccato ^-1 2x√(1 –x ² )
3peccato ^-1 x = peccato ^-1 (3x-4x ³ )
3cos ^-1 x = cos ^-1 (4x ³ – 3x)
3tan ^-1 x = così ^-1 ((3x-x ³ /1 – 3x ² ))
senza ^-1 x + peccato ^-1 y = senza ^-1 { x√(1 – y ² ) + y√(1 – x ² )}
senza ^-1 x – peccato ^-1 y = senza ^-1 { x√(1 – y ² ) – y√(1 – x ² )}
cos ^-1 x + cos ^-1 y = cos ^-1 [xy – √{(1 – x ² )(1 – e ² )}]
cos ^-1 x – cos ^-1 y = cos ^-1 [xy + √{(1 – x ² )(1 – e ² )}
COSÌ ^-1 x + abbronzatura ^-1 y = così ^-1 (x + y/1 – xy)
COSÌ ^-1 x – quindi ^-1 y = così ^-1 (x – y/1 + xy)
COSÌ ^-1 x + abbronzatura ^-1 e +abbronzatura ^-1 z = così ^-1 (x + y + z – xyz)/(1 – xy – yz – zx)

Le persone visualizzano anche:

Trigonometria in matematica | Tabella, Formule, Identità

Elenco di tutte le identità trigonometriche

Funzioni trigonometriche inverse

Grafici di funzioni trigonometriche inverse

Esempi di problemi sulle identità trigonometriche inverse

Domanda 1: prova senza ^-1 x = sec ^-1 1/√(1-x ² )

Soluzione:

Lasciamo senza ^-1 x = y

⇒ sin y = x , (poiché sin y = perpendicolare/ipotenusa ⇒ cos y = √(1- perpendicolare ² )/ipotenusa )

⇒ cos y = √(1 – x ² ), qui ipotenusa = 1

⇒ sec y = 1/cos y

⇒ sec y = 1/√(1 – x ² )

⇒ y = sec ^-1 1/√(1 –x ² )

⇒ senza ^-1 x = sec ^-1 1/√(1 –x ² )

Quindi, dimostrato.

Domanda 2: provalo ^-1 x = cosec ^-1 √(1+x ² )/X

Soluzione:

Lasciamo stare ^-1 x = y

⇒ tan y = x, perpendicolare = x e base = 1

⇒ sin y = x/√(x ² + 1) , (poiché ipotenusa = √(perpendicolare ² +fondo ² ) )

⇒ cosec y = 1/sen y

⇒ cosec y = √(x ² +1)/x

⇒ y = cosec ^-1 √(x ² +1)/x

⇒ così ^-1 x = cosec ^-1 √(x ² +1)/x

Quindi, dimostrato.

Domanda 3: Valuta te stesso come ^-1 X)

Soluzione:

Lasciamo cos ^-1 x = y

⇒ cos y = x , base = x e ipotenusa = 1 quindi sin y = √(1 – x ² )/1

⇒ tan y = sin y/ cos y

⇒ tan y = √(1 – x ² )/X

⇒ y = così ^-1 √(1 –x ² )/X

⇒ cos ^-1 x = così ^-1 √(1 –x ² )/X

Pertanto, tan(cos ^-1 x) = tan(tan ^-1 √(1 –x ² )/x ) = √(1 – x ² )/X.

Domanda 4: sì ^-1 √(peccato x) + lettino ^-1 √(peccato x) = y. Trova cos e.

Soluzione:

Conosciamo quell'abbronzatura ^-1 x + lettino ^-1 x = /2 quindi confrontando questa identità con l'equazione data nella domanda otteniamo y = π/2

Pertanto, cos y = cos π/2 = 0.

Domanda 5: sì ^-1 (1 – x)/(1 + x) = (1/2)tan ^-1 x, x> 0. Risolvi per x.

Soluzione:

COSÌ ^-1 (1 – x)/(1 + x) = (1/2)tan ^-1 X

⇒ 2abbronzatura ^-1 (1 – x)/(1 + x) = tan ^-1 x…(1)

Lo sappiamo, 2tan ^-1 x = così ^-1 2x/(1 –x ² ).

Pertanto, LHS dell'equazione (1) può essere scritto come

COSÌ ^-1 [ { 2(1 – x)/(1 + x)}/{ 1 – [(1 – x)(1 + x)] ² }]

= così ^-1 [ {2(1 – x)(1 + x)} / { (1 + x) ² – (1 – x) ² }]

= così ^-1 [ 2(1 –x ² )/(4x)]

= così ^-1 (1-x ² )/(2x)

Poiché, LHS = RHS quindi

COSÌ ^-1 (1-x ² )/(2x) = marrone chiaro ^-1 X

⇒ (1 –x ² )/2x = x

⇒ 1 –x ² = 2x ²

⇒ 3x ² = 1

⇒ x = ± 1/√3

Poiché x deve essere maggiore di 0, x = 1/√3 è la risposta accettabile.

Domanda 6: Provalo ^-1 √x = (1/2)cos ^-1 (1 – x)/(1 + x)

Soluzione:

Lasciamo stare ^-1 √x = y

⇒ tan y = √x

⇒ così ² y = x

Perciò,

Dx = (1/2)cos ^-1 (1- quindi ² y)/(1 + marrone chiaro ² E)

= (1/2)cos ^-1 (cos ² e senza ² y)/(cos ² e + senza ² E)

= (1/2)cos ^-1 (cos ² e senza ² E)

= (1/2)cos ^-1 (cos 2 anni)

= (1/2)(2 anni)

= e

= così ^-1 √x

= sinistra

Quindi, dimostrato.

Domanda 7: sì ^-1 (2x)/(1 –x ² ) + lettino ^-1 (1-x ² )/(2x) = π/2, -1

Soluzioni:

COSÌ ^-1 (2x)/(1 –x ² ) + lettino ^-1 (1-x ² )/(2x) = π/2

⇒ così ^-1 (2x)/(1 –x ² ) + così ^-1 (2x)/(1 –x ² ) = π/2

⇒ 2abbronzatura ^-1 (2x)/(1 –x ² ) = ∏/2

⇒ così ^-1 (2x)/(1 –x ² ) = ∏/4

⇒ (2x)/(1 – x ² ) = marrone chiaro ∏/4

⇒ (2x)/(1 – x ² ) = 1

⇒ 2x = 1 – x ²

⇒x ² +2x-1 = 0

⇒ x = [-2 ± √(2 ² – 4(1)(-1))] / 2

⇒ x = [-2 ± √8] / 2

⇒ x = -1 ± √2

⇒ x = -1 + √2 oppure x = -1 – √2

Ma secondo la domanda x ∈ (-1, 1) quindi per l'equazione data l'insieme delle soluzioni è x ∈ ∅.

Domanda 8: sì ^-1 1/(1 + 1,2) + abbronzatura ^-1 1/(1+2,3)+…+ COSÌ ^-1 1/(1 + n(n + 1)) = tan ^-1 X. Risolvi per x.

Soluzione:

COSÌ ^-1 1/(1 + 1,2) + abbronzatura ^-1 1/(1 + 2,3) + … + tan ^-1 1/(1 + n(n + 1)) = tan ^-1 X

⇒ così ^-1 (2 – 1)/(1 + 1,2) + abbronzatura ^-1 (3 – 2)/(1 + 2,3) + … + così ^-1 (n + 1 – n)/(1 + n(n + 1)) = tan ^-1 X

⇒ (quindi ^-1 2 – quindi ^-1 1) + (così ^-1 3 – quindi ^-1 2) + … + (così ^-1 (n + 1) – quindi ^-1 n) = così ^-1 X

⇒ così ^-1 (n + 1) – quindi ^-1 1 = così ^-1 X

⇒ così ^-1 n/(1 + (n + 1).1) = tan ^-1 X

⇒ così ^-1 n/(n + 2) = tan ^-1 X

⇒ x = n/(n + 2)

Domanda 9: Se 2tan ^-1 (senza x) = così ^-1 (2sec x) quindi risolvi per x.

Soluzione:

2tan ^-1 (senza x) = così ^-1 (2 secondi x)

⇒ così ^-1 (2 peccato x)/(1 – peccato ² x) = così ^-1 (2/cos x)

⇒ (2peccato x)/(1 – peccato ² x) = 2/cos x

⇒ peccato x/cos ² x = 1/cosx

⇒ peccato x cos x = cos ² X

⇒ peccato x cos x – cos ² x = 0

⇒ cos x(sen x – cos x) = 0

⇒ cos x = 0 oppure sin x – cos x = 0

⇒ cos x = cos π/2 o tan x = tan π/4

⇒ x = π/2 oppure x = π/4

Ma per x = π/2 l'equazione data non esiste quindi x = π/4 è l'unica soluzione.

Domanda 10: Dimostra quella branda ^-1 [ {√(1 + peccato x) + √(1 – peccato x)}/{√(1 + peccato x) – √(1 – peccato x)}] = x/2, x ∈ (0, π/4 )

Soluzione:

Sia quindi x = 2y

LHS = lettino ^-1 [{√(1+peccato 2a) + √(1-peccato 2a)}/{√(1+peccato 2a) – √(1-peccato 2a)}]

= lettino ^-1 [{√(cos ² e + senza ² y + 2sen y cos y) + √(cos ² e + senza ² y – 2sen y cos y)}/{√(cos ² e + senza ² y + 2sen y cos y) – √(cos ² e + senza ² y – 2sen e cos y)} ]

= lettino ^-1 [{√(cos y + sin y) ² + √(cos y – peccato y) ² } / {√(cos y + sin y) ² – √(cos e – peccato e) ² }]

= lettino ^-1 [(cos y + sin y + cos y – sin y )/(cos y + sin y – cos y + sin y)]

= lettino ^-1 (2cos y)/(2sen y)

= lettino ^-1 (culla e)

= e

=x/2.

Problemi pratici sulle identità trigonometriche inverse

Problema 1: Risolvi x nell'equazione sin ^-1 (x) + cos ^-1 (x) = π/2

Problema 2: Dimostra che sei abbronzato ^-1 (1) + così ^-1 (2) + così ^-1 (3) = pag

Problema 3: valutare cos⁡(senza ^-1 (0,5))

Problema 4: Se abbronzato ^-1 (x) + abbronzatura ^-1 (2x) = π/4, quindi trova x

Domande frequenti sulle identità trigonometriche inverse

Cosa sono le funzioni trigonometriche inverse?

Le funzioni trigonometriche inverse sono le funzioni inverse delle funzioni trigonometriche di base (seno, coseno, tangente, cosecante, secante e cotangente). Servono per trovare gli angoli corrispondenti a determinati rapporti trigonometrici.

Perché le funzioni trigonometriche inverse sono importanti?

Le funzioni trigonometriche inverse sono essenziali in vari campi come la geometria, l'ingegneria e la fisica perché aiutano a determinare gli angoli dai rapporti trigonometrici, il che è fondamentale per risolvere molti problemi pratici.

Quali sono i domini e gli intervalli delle funzioni trigonometriche inverse?

Ciascuna funzione trigonometrica inversa ha domini e intervalli specifici:

S In ^-1 (x) : Dominio [-1, 1] e Intervallo [- π/2, π/2]

cos ^-1 (x) : Dominio [-1, 1] e Intervallo [ 0, π]

quindi⁡ ^-1 (x) : Dominio R e intervallo (- π/2, π/2)

Le funzioni trigonometriche inverse possono essere utilizzate nel calcolo?

Sì, le funzioni trigonometriche inverse sono spesso utilizzate nel calcolo per l'integrazione e la differenziazione. Sono particolarmente utili per integrare funzioni che coinvolgono espressioni trigonometriche.