Egy elem pozíciója stabil rendezés után

 #practiceLinkDiv { display: none !important; }
#practiceLinkDiv { display: none !important; } Adott egy egész számokból álló tömb, amely duplikált elemeket tartalmazhat, ennek a tömbnek egy eleme adott nekünk, meg kell mondanunk ennek az elemnek a végső pozícióját a tömbben, ha stabil rendezési algoritmust alkalmazunk.
Példák:
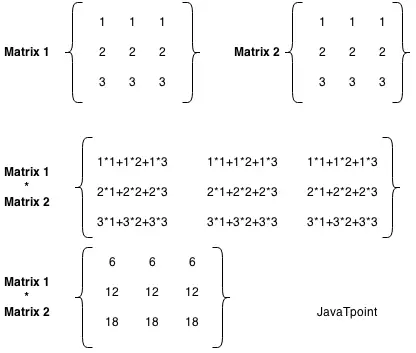
Input : arr[] = [3 4 3 5 2 3 4 3 1 5] index = 5 Output : 4 Element initial index – 5 (third 3) After sorting array by stable sorting algorithm we get array as shown below [1(8) 2(4) 3(0) 3(2) 3(5) 3(7) 4(1) 4(6) 5(3) 5(9)] with their initial indices shown in parentheses next to them Element's index after sorting = 4Recommended Practice Stabil rendezés és pozíció Próbáld ki!
A probléma megoldásának egyik egyszerű módja bármely stabil rendezési algoritmus, például Beszúrás rendezése A rendezés megy stb, majd megkapjuk az adott elem új indexét, de ezt a problémát a tömb rendezése nélkül is megoldhatjuk.
Egy elem helyzetét egy rendezett tömbben csak azok az elemek határozzák meg, amelyek kisebbek az adott elemnél. Minden adott elemnél kisebb tömbelemet számolunk, és azoknál az elemeknél, amelyek egyenlők az adott elem indexe előtt előforduló elemekkel, a kisebb elemek számába beszámítjuk, ez biztosítja az eredmény indexének stabilitását.
A fenti megközelítés megvalósításához szükséges egyszerű kódot az alábbiakban valósítjuk meg:
C++ // C++ program to get index of array element in // sorted array #include using namespace std ; // Method returns the position of arr[idx] after // performing stable-sort on array int getIndexInSortedArray ( int arr [] int n int idx ) { /* Count of elements smaller than current element plus the equal element occurring before given index*/ int result = 0 ; for ( int i = 0 ; i < n ; i ++ ) { // If element is smaller then increase // the smaller count if ( arr [ i ] < arr [ idx ]) result ++ ; // If element is equal then increase count // only if it occurs before if ( arr [ i ] == arr [ idx ] && i < idx ) result ++ ; } return result ; } // Driver code to test above methods int main () { int arr [] = { 3 4 3 5 2 3 4 3 1 5 }; int n = sizeof ( arr ) / sizeof ( arr [ 0 ]); int idxOfEle = 5 ; cout < < getIndexInSortedArray ( arr n idxOfEle ); return 0 ; }
Java // Java program to get index of array // element in sorted array class ArrayIndex { // Method returns the position of // arr[idx] after performing stable-sort // on array static int getIndexInSortedArray ( int arr [] int n int idx ) { /* Count of elements smaller than current element plus the equal element occurring before given index*/ int result = 0 ; for ( int i = 0 ; i < n ; i ++ ) { // If element is smaller then // increase the smaller count if ( arr [ i ] < arr [ idx ] ) result ++ ; // If element is equal then increase // count only if it occurs before if ( arr [ i ] == arr [ idx ] && i < idx ) result ++ ; } return result ; } // Driver code to test above methods public static void main ( String [] args ) { int arr [] = { 3 4 3 5 2 3 4 3 1 5 }; int n = arr . length ; int idxOfEle = 5 ; System . out . println ( getIndexInSortedArray ( arr n idxOfEle )); } } // This code is contributed by Raghav sharma
Python3 # Python program to get index of array element in # sorted array # Method returns the position of arr[idx] after # performing stable-sort on array def getIndexInSortedArray ( arr n idx ): # Count of elements smaller than current # element plus the equal element occurring # before given index result = 0 for i in range ( n ): # If element is smaller then increase # the smaller count if ( arr [ i ] < arr [ idx ]): result += 1 # If element is equal then increase count # only if it occurs before if ( arr [ i ] == arr [ idx ] and i < idx ): result += 1 return result ; # Driver code to test above methods arr = [ 3 4 3 5 2 3 4 3 1 5 ] n = len ( arr ) idxOfEle = 5 print ( getIndexInSortedArray ( arr n idxOfEle )) # Contributed by: Afzal Ansari
C# // C# program to get index of array // element in sorted array using System ; class ArrayIndex { // Method returns the position of // arr[idx] after performing stable-sort // on array static int getIndexInSortedArray ( int [] arr int n int idx ) { /* Count of elements smaller than current element plus the equal element occurring before given index*/ int result = 0 ; for ( int i = 0 ; i < n ; i ++ ) { // If element is smaller then // increase the smaller count if ( arr [ i ] < arr [ idx ]) result ++ ; // If element is equal then increase // count only if it occurs before if ( arr [ i ] == arr [ idx ] && i < idx ) result ++ ; } return result ; } // Driver code to test above methods public static void Main () { int [] arr = { 3 4 3 5 2 3 4 3 1 5 }; int n = arr . Length ; int idxOfEle = 5 ; Console . WriteLine ( getIndexInSortedArray ( arr n idxOfEle )); } } // This code is contributed by vt_m
PHP // PHP program to get index of // array element in sorted array // Method returns the position of // arr[idx] after performing // stable-sort on array function getIndexInSortedArray ( $arr $n $idx ) { /* Count of elements smaller than current element plus the equal element occurring before given index */ $result = 0 ; for ( $i = 0 ; $i < $n ; $i ++ ) { // If element is smaller then // increase the smaller count if ( $arr [ $i ] < $arr [ $idx ]) $result ++ ; // If element is equal then // increase count only if // it occurs before if ( $arr [ $i ] == $arr [ $idx ] and $i < $idx ) $result ++ ; } return $result ; } // Driver Code $arr = array ( 3 4 3 5 2 3 4 3 1 5 ); $n = count ( $arr ); $idxOfEle = 5 ; echo getIndexInSortedArray ( $arr $n $idxOfEle ); // This code is contributed by anuj_67. ?>
JavaScript < script > // JavaScript program to get index of array // element in sorted array // Method returns the position of // arr[idx] after performing stable-sort // on array function getIndexInSortedArray ( arr n idx ) { /* Count of elements smaller than current element plus the equal element occurring before given index*/ let result = 0 ; for ( let i = 0 ; i < n ; i ++ ) { // If element is smaller then // increase the smaller count if ( arr [ i ] < arr [ idx ]) result ++ ; // If element is equal then increase // count only if it occurs before if ( arr [ i ] == arr [ idx ] && i < idx ) result ++ ; } return result ; } // Driver Code let arr = [ 3 4 3 5 2 3 4 3 1 5 ]; let n = arr . length ; let idxOfEle = 5 ; document . write ( getIndexInSortedArray ( arr n idxOfEle )); // This code is contributed by code_hunt. < /script>
Kimenet
4
Időbeli összetettség: On) ahol n a tömb mérete.
Segédtér: O(1)
Kvíz létrehozása