Minimális lépések a cél eléréséhez egy lovag által | 2. készlet

Adott egy N x N méretű négyzetes sakktábla, a lovag pozíciója és a célpont helyzete azt a feladatot kapja, hogy megtudja, hogy egy lovag milyen minimális lépéseket tesz a célpozíció eléréséhez.

Példák:
Input : (2 4) - knight's position (6 4) - target cell Output : 2 Input : (4 5) (1 1) Output : 3
A fenti probléma megoldására szolgáló BFS-megközelítést már tárgyaltuk a előző hozzászólás. Ebben a bejegyzésben egy dinamikus programozási megoldást tárgyalunk.
A megközelítés magyarázata:
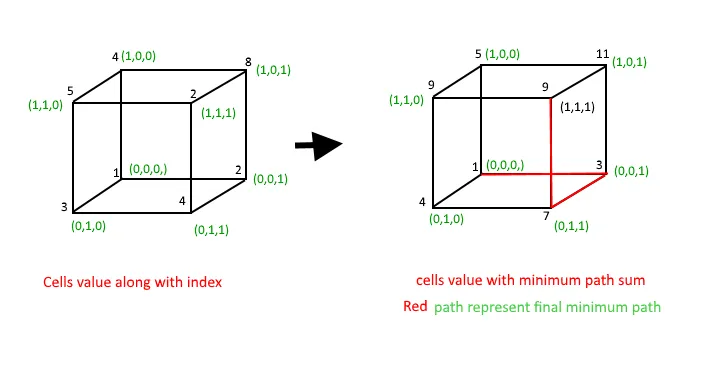
Legyen egy 8 x 8 cellás sakktábla. Tegyük fel, hogy a lovag a (3 3) pontban van, a cél pedig a (7 8) helyen van. A lovag jelenlegi pozíciójából 8 lépés lehetséges, azaz (2 1) (1 2) (4 1) (1 4) (5 2) (2 5) (5 4) (4 5). De ezek közül csak két mozdulat (5 4) és (4 5) lesz a cél felé, a többi pedig távolodik a céltól. Tehát a minimális lépések megtalálásához lépjen a (4 5) vagy az (5 4) pontra. Most számítsa ki a (4 5) és (5 4) értékekből a cél eléréséhez megtett minimális lépéseket. Ezt dinamikus programozással számítják ki. Így ez a (3 3) és (7 8) közötti minimális lépéseket eredményezi.
Legyen egy 8 x 8 cellás sakktábla. Most tegyük fel, hogy a lovag a (4 3) pontban van, a cél pedig a (4 7) pontban van. 8 mozgás lehetséges, de a cél felé csak 4 lépés van, azaz (5 5) (3 5) (2 4) (6 4). Mivel (5 5) ekvivalens (3 5) és (2 4) (6 4). Tehát ebből a 4 pontból 2 pontra váltható. (5 5) és (6 4) (itt) felvétele. Most számítsa ki a két pontból megtett minimális lépéseket a cél eléréséhez. Ezt dinamikus programozással számítják ki. Így ez a (4 3) és (4 7) közötti minimális lépéseket eredményezi.
Kivétel: Amikor a lovag a sarokban lesz, és a cél olyan, hogy az x és y koordináták különbsége a lovag pozíciójával (1 1) vagy fordítva. Ekkor a minimális lépésszám 4 lesz.
Dinamikus programozási egyenlet:
1) dp[diffOfX][diffOfY] a lovag pozíciójától a célpontig megtett minimális lépések száma.
2) dp[diffOfX][diffOfY] = dp[diffOfY][diffOfX] .
ahol diffOfX = különbség a lovag x-koordinátája és a célpont x-koordinátája között
diffOfY = különbség a lovag y-koordinátája és a célpont y-koordinátája között
Az alábbiakban bemutatjuk a fenti megközelítés megvalósítását:
// C++ code for minimum steps for // a knight to reach target position #include using namespace std ; // initializing the matrix. int dp [ 8 ][ 8 ] = { 0 }; int getsteps ( int x int y int tx int ty ) { // if knight is on the target // position return 0. if ( x == tx && y == ty ) return dp [ 0 ][ 0 ]; else { // if already calculated then return // that value. Taking absolute difference. if ( dp [ abs ( x - tx )][ abs ( y - ty )] != 0 ) return dp [ abs ( x - tx )][ abs ( y - ty )]; else { // there will be two distinct positions // from the knight towards a target. // if the target is in same row or column // as of knight then there can be four // positions towards the target but in that // two would be the same and the other two // would be the same. int x1 y1 x2 y2 ; // (x1 y1) and (x2 y2) are two positions. // these can be different according to situation. // From position of knight the chess board can be // divided into four blocks i.e.. N-E E-S S-W W-N . if ( x <= tx ) { if ( y <= ty ) { x1 = x + 2 ; y1 = y + 1 ; x2 = x + 1 ; y2 = y + 2 ; } else { x1 = x + 2 ; y1 = y - 1 ; x2 = x + 1 ; y2 = y - 2 ; } } else { if ( y <= ty ) { x1 = x - 2 ; y1 = y + 1 ; x2 = x - 1 ; y2 = y + 2 ; } else { x1 = x - 2 ; y1 = y - 1 ; x2 = x - 1 ; y2 = y - 2 ; } } // ans will be 1 + minimum of steps // required from (x1 y1) and (x2 y2). dp [ abs ( x - tx )][ abs ( y - ty )] = min ( getsteps ( x1 y1 tx ty ) getsteps ( x2 y2 tx ty )) + 1 ; // exchanging the coordinates x with y of both // knight and target will result in same ans. dp [ abs ( y - ty )][ abs ( x - tx )] = dp [ abs ( x - tx )][ abs ( y - ty )]; return dp [ abs ( x - tx )][ abs ( y - ty )]; } } } // Driver Code int main () { int i n x y tx ty ans ; // size of chess board n*n n = 100 ; // (x y) coordinate of the knight. // (tx ty) coordinate of the target position. x = 4 ; y = 5 ; tx = 1 ; ty = 1 ; // (Exception) these are the four corner points // for which the minimum steps is 4. if (( x == 1 && y == 1 && tx == 2 && ty == 2 ) || ( x == 2 && y == 2 && tx == 1 && ty == 1 )) ans = 4 ; else if (( x == 1 && y == n && tx == 2 && ty == n - 1 ) || ( x == 2 && y == n - 1 && tx == 1 && ty == n )) ans = 4 ; else if (( x == n && y == 1 && tx == n - 1 && ty == 2 ) || ( x == n - 1 && y == 2 && tx == n && ty == 1 )) ans = 4 ; else if (( x == n && y == n && tx == n - 1 && ty == n - 1 ) || ( x == n - 1 && y == n - 1 && tx == n && ty == n )) ans = 4 ; else { // dp[a][b] here a b is the difference of // x & tx and y & ty respectively. dp [ 1 ][ 0 ] = 3 ; dp [ 0 ][ 1 ] = 3 ; dp [ 1 ][ 1 ] = 2 ; dp [ 2 ][ 0 ] = 2 ; dp [ 0 ][ 2 ] = 2 ; dp [ 2 ][ 1 ] = 1 ; dp [ 1 ][ 2 ] = 1 ; ans = getsteps ( x y tx ty ); } cout < < ans < < endl ; return 0 ; }
Java //Java code for minimum steps for // a knight to reach target position public class GFG { // initializing the matrix. static int dp [][] = new int [ 8 ][ 8 ] ; static int getsteps ( int x int y int tx int ty ) { // if knight is on the target // position return 0. if ( x == tx && y == ty ) { return dp [ 0 ][ 0 ] ; } else // if already calculated then return // that value. Taking absolute difference. if ( dp [ Math . abs ( x - tx ) ][ Math . abs ( y - ty ) ] != 0 ) { return dp [ Math . abs ( x - tx ) ][ Math . abs ( y - ty ) ] ; } else { // there will be two distinct positions // from the knight towards a target. // if the target is in same row or column // as of knight then there can be four // positions towards the target but in that // two would be the same and the other two // would be the same. int x1 y1 x2 y2 ; // (x1 y1) and (x2 y2) are two positions. // these can be different according to situation. // From position of knight the chess board can be // divided into four blocks i.e.. N-E E-S S-W W-N . if ( x <= tx ) { if ( y <= ty ) { x1 = x + 2 ; y1 = y + 1 ; x2 = x + 1 ; y2 = y + 2 ; } else { x1 = x + 2 ; y1 = y - 1 ; x2 = x + 1 ; y2 = y - 2 ; } } else if ( y <= ty ) { x1 = x - 2 ; y1 = y + 1 ; x2 = x - 1 ; y2 = y + 2 ; } else { x1 = x - 2 ; y1 = y - 1 ; x2 = x - 1 ; y2 = y - 2 ; } // ans will be 1 + minimum of steps // required from (x1 y1) and (x2 y2). dp [ Math . abs ( x - tx ) ][ Math . abs ( y - ty ) ] = Math . min ( getsteps ( x1 y1 tx ty ) getsteps ( x2 y2 tx ty )) + 1 ; // exchanging the coordinates x with y of both // knight and target will result in same ans. dp [ Math . abs ( y - ty ) ][ Math . abs ( x - tx ) ] = dp [ Math . abs ( x - tx ) ][ Math . abs ( y - ty ) ] ; return dp [ Math . abs ( x - tx ) ][ Math . abs ( y - ty ) ] ; } } // Driver Code static public void main ( String [] args ) { int i n x y tx ty ans ; // size of chess board n*n n = 100 ; // (x y) coordinate of the knight. // (tx ty) coordinate of the target position. x = 4 ; y = 5 ; tx = 1 ; ty = 1 ; // (Exception) these are the four corner points // for which the minimum steps is 4. if (( x == 1 && y == 1 && tx == 2 && ty == 2 ) || ( x == 2 && y == 2 && tx == 1 && ty == 1 )) { ans = 4 ; } else if (( x == 1 && y == n && tx == 2 && ty == n - 1 ) || ( x == 2 && y == n - 1 && tx == 1 && ty == n )) { ans = 4 ; } else if (( x == n && y == 1 && tx == n - 1 && ty == 2 ) || ( x == n - 1 && y == 2 && tx == n && ty == 1 )) { ans = 4 ; } else if (( x == n && y == n && tx == n - 1 && ty == n - 1 ) || ( x == n - 1 && y == n - 1 && tx == n && ty == n )) { ans = 4 ; } else { // dp[a][b] here a b is the difference of // x & tx and y & ty respectively. dp [ 1 ][ 0 ] = 3 ; dp [ 0 ][ 1 ] = 3 ; dp [ 1 ][ 1 ] = 2 ; dp [ 2 ][ 0 ] = 2 ; dp [ 0 ][ 2 ] = 2 ; dp [ 2 ][ 1 ] = 1 ; dp [ 1 ][ 2 ] = 1 ; ans = getsteps ( x y tx ty ); } System . out . println ( ans ); } } /*This code is contributed by PrinciRaj1992*/
Python3 # Python3 code for minimum steps for # a knight to reach target position # initializing the matrix. dp = [[ 0 for i in range ( 8 )] for j in range ( 8 )]; def getsteps ( x y tx ty ): # if knight is on the target # position return 0. if ( x == tx and y == ty ): return dp [ 0 ][ 0 ]; # if already calculated then return # that value. Taking absolute difference. elif ( dp [ abs ( x - tx )][ abs ( y - ty )] != 0 ): return dp [ abs ( x - tx )][ abs ( y - ty )]; else : # there will be two distinct positions # from the knight towards a target. # if the target is in same row or column # as of knight then there can be four # positions towards the target but in that # two would be the same and the other two # would be the same. x1 y1 x2 y2 = 0 0 0 0 ; # (x1 y1) and (x2 y2) are two positions. # these can be different according to situation. # From position of knight the chess board can be # divided into four blocks i.e.. N-E E-S S-W W-N . if ( x <= tx ): if ( y <= ty ): x1 = x + 2 ; y1 = y + 1 ; x2 = x + 1 ; y2 = y + 2 ; else : x1 = x + 2 ; y1 = y - 1 ; x2 = x + 1 ; y2 = y - 2 ; elif ( y <= ty ): x1 = x - 2 ; y1 = y + 1 ; x2 = x - 1 ; y2 = y + 2 ; else : x1 = x - 2 ; y1 = y - 1 ; x2 = x - 1 ; y2 = y - 2 ; # ans will be 1 + minimum of steps # required from (x1 y1) and (x2 y2). dp [ abs ( x - tx )][ abs ( y - ty )] = min ( getsteps ( x1 y1 tx ty ) getsteps ( x2 y2 tx ty )) + 1 ; # exchanging the coordinates x with y of both # knight and target will result in same ans. dp [ abs ( y - ty )][ abs ( x - tx )] = dp [ abs ( x - tx )][ abs ( y - ty )]; return dp [ abs ( x - tx )][ abs ( y - ty )]; # Driver Code if __name__ == '__main__' : # size of chess board n*n n = 100 ; # (x y) coordinate of the knight. # (tx ty) coordinate of the target position. x = 4 ; y = 5 ; tx = 1 ; ty = 1 ; # (Exception) these are the four corner points # for which the minimum steps is 4. if (( x == 1 and y == 1 and tx == 2 and ty == 2 ) or ( x == 2 and y == 2 and tx == 1 and ty == 1 )): ans = 4 ; elif (( x == 1 and y == n and tx == 2 and ty == n - 1 ) or ( x == 2 and y == n - 1 and tx == 1 and ty == n )): ans = 4 ; elif (( x == n and y == 1 and tx == n - 1 and ty == 2 ) or ( x == n - 1 and y == 2 and tx == n and ty == 1 )): ans = 4 ; elif (( x == n and y == n and tx == n - 1 and ty == n - 1 ) or ( x == n - 1 and y == n - 1 and tx == n and ty == n )): ans = 4 ; else : # dp[a][b] here a b is the difference of # x & tx and y & ty respectively. dp [ 1 ][ 0 ] = 3 ; dp [ 0 ][ 1 ] = 3 ; dp [ 1 ][ 1 ] = 2 ; dp [ 2 ][ 0 ] = 2 ; dp [ 0 ][ 2 ] = 2 ; dp [ 2 ][ 1 ] = 1 ; dp [ 1 ][ 2 ] = 1 ; ans = getsteps ( x y tx ty ); print ( ans ); # This code is contributed by PrinciRaj1992
C# // C# code for minimum steps for // a knight to reach target position using System ; public class GFG { // initializing the matrix. static int [ ] dp = new int [ 8 8 ]; static int getsteps ( int x int y int tx int ty ) { // if knight is on the target // position return 0. if ( x == tx && y == ty ) { return dp [ 0 0 ]; } else // if already calculated then return // that value. Taking Absolute difference. if ( dp [ Math . Abs ( x - tx ) Math . Abs ( y - ty )] != 0 ) { return dp [ Math . Abs ( x - tx ) Math . Abs ( y - ty )]; } else { // there will be two distinct positions // from the knight towards a target. // if the target is in same row or column // as of knight then there can be four // positions towards the target but in that // two would be the same and the other two // would be the same. int x1 y1 x2 y2 ; // (x1 y1) and (x2 y2) are two positions. // these can be different according to situation. // From position of knight the chess board can be // divided into four blocks i.e.. N-E E-S S-W W-N . if ( x <= tx ) { if ( y <= ty ) { x1 = x + 2 ; y1 = y + 1 ; x2 = x + 1 ; y2 = y + 2 ; } else { x1 = x + 2 ; y1 = y - 1 ; x2 = x + 1 ; y2 = y - 2 ; } } else if ( y <= ty ) { x1 = x - 2 ; y1 = y + 1 ; x2 = x - 1 ; y2 = y + 2 ; } else { x1 = x - 2 ; y1 = y - 1 ; x2 = x - 1 ; y2 = y - 2 ; } // ans will be 1 + minimum of steps // required from (x1 y1) and (x2 y2). dp [ Math . Abs ( x - tx ) Math . Abs ( y - ty )] = Math . Min ( getsteps ( x1 y1 tx ty ) getsteps ( x2 y2 tx ty )) + 1 ; // exchanging the coordinates x with y of both // knight and target will result in same ans. dp [ Math . Abs ( y - ty ) Math . Abs ( x - tx )] = dp [ Math . Abs ( x - tx ) Math . Abs ( y - ty )]; return dp [ Math . Abs ( x - tx ) Math . Abs ( y - ty )]; } } // Driver Code static public void Main () { int i n x y tx ty ans ; // size of chess board n*n n = 100 ; // (x y) coordinate of the knight. // (tx ty) coordinate of the target position. x = 4 ; y = 5 ; tx = 1 ; ty = 1 ; // (Exception) these are the four corner points // for which the minimum steps is 4. if (( x == 1 && y == 1 && tx == 2 && ty == 2 ) || ( x == 2 && y == 2 && tx == 1 && ty == 1 )) { ans = 4 ; } else if (( x == 1 && y == n && tx == 2 && ty == n - 1 ) || ( x == 2 && y == n - 1 && tx == 1 && ty == n )) { ans = 4 ; } else if (( x == n && y == 1 && tx == n - 1 && ty == 2 ) || ( x == n - 1 && y == 2 && tx == n && ty == 1 )) { ans = 4 ; } else if (( x == n && y == n && tx == n - 1 && ty == n - 1 ) || ( x == n - 1 && y == n - 1 && tx == n && ty == n )) { ans = 4 ; } else { // dp[a b] here a b is the difference of // x & tx and y & ty respectively. dp [ 1 0 ] = 3 ; dp [ 0 1 ] = 3 ; dp [ 1 1 ] = 2 ; dp [ 2 0 ] = 2 ; dp [ 0 2 ] = 2 ; dp [ 2 1 ] = 1 ; dp [ 1 2 ] = 1 ; ans = getsteps ( x y tx ty ); } Console . WriteLine ( ans ); } } /*This code is contributed by PrinciRaj1992*/
JavaScript < script > // JavaScript code for minimum steps for // a knight to reach target position // initializing the matrix. let dp = new Array ( 8 ) for ( let i = 0 ; i < 8 ; i ++ ){ dp [ i ] = new Array ( 8 ). fill ( 0 ) } function getsteps ( x y tx ty ) { // if knight is on the target // position return 0. if ( x == tx && y == ty ) return dp [ 0 ][ 0 ]; else { // if already calculated then return // that value. Taking absolute difference. if ( dp [( Math . abs ( x - tx ))][( Math . abs ( y - ty ))] != 0 ) return dp [( Math . abs ( x - tx ))][( Math . abs ( y - ty ))]; else { // there will be two distinct positions // from the knight towards a target. // if the target is in same row or column // as of knight then there can be four // positions towards the target but in that // two would be the same and the other two // would be the same. let x1 y1 x2 y2 ; // (x1 y1) and (x2 y2) are two positions. // these can be different according to situation. // From position of knight the chess board can be // divided into four blocks i.e.. N-E E-S S-W W-N . if ( x <= tx ) { if ( y <= ty ) { x1 = x + 2 ; y1 = y + 1 ; x2 = x + 1 ; y2 = y + 2 ; } else { x1 = x + 2 ; y1 = y - 1 ; x2 = x + 1 ; y2 = y - 2 ; } } else { if ( y <= ty ) { x1 = x - 2 ; y1 = y + 1 ; x2 = x - 1 ; y2 = y + 2 ; } else { x1 = x - 2 ; y1 = y - 1 ; x2 = x - 1 ; y2 = y - 2 ; } } // ans will be 1 + minimum of steps // required from (x1 y1) and (x2 y2). dp [( Math . abs ( x - tx ))][( Math . abs ( y - ty ))] = Math . min ( getsteps ( x1 y1 tx ty ) getsteps ( x2 y2 tx ty )) + 1 ; // exchanging the coordinates x with y of both // knight and target will result in same ans. dp [( Math . abs ( y - ty ))][( Math . abs ( x - tx ))] = dp [( Math . abs ( x - tx ))][( Math . abs ( y - ty ))]; return dp [( Math . abs ( x - tx ))][( Math . abs ( y - ty ))]; } } } // Driver Code let i n x y tx ty ans ; // size of chess board n*n n = 100 ; // (x y) coordinate of the knight. // (tx ty) coordinate of the target position. x = 4 ; y = 5 ; tx = 1 ; ty = 1 ; // (Exception) these are the four corner points // for which the minimum steps is 4. if (( x == 1 && y == 1 && tx == 2 && ty == 2 ) || ( x == 2 && y == 2 && tx == 1 && ty == 1 )) ans = 4 ; else if (( x == 1 && y == n && tx == 2 && ty == n - 1 ) || ( x == 2 && y == n - 1 && tx == 1 && ty == n )) ans = 4 ; else if (( x == n && y == 1 && tx == n - 1 && ty == 2 ) || ( x == n - 1 && y == 2 && tx == n && ty == 1 )) ans = 4 ; else if (( x == n && y == n && tx == n - 1 && ty == n - 1 ) || ( x == n - 1 && y == n - 1 && tx == n && ty == n )) ans = 4 ; else { // dp[a][b] here a b is the difference of // x & tx and y & ty respectively. dp [ 1 ][ 0 ] = 3 ; dp [ 0 ][ 1 ] = 3 ; dp [ 1 ][ 1 ] = 2 ; dp [ 2 ][ 0 ] = 2 ; dp [ 0 ][ 2 ] = 2 ; dp [ 2 ][ 1 ] = 1 ; dp [ 1 ][ 2 ] = 1 ; ans = getsteps ( x y tx ty ); } document . write ( ans ' ' ); // This code is contributed by shinjanpatra. < /script>
Kimenet:
3
Időbeli összetettség: O(N * M) ahol N a sorok teljes száma, M pedig az oszlopok száma
Kiegészítő tér: O(N*M)