Hierholzerov algoritam za usmjereni graf

S obzirom na usmjereni Eulerov graf zadatak je ispisati Eulerov krug . Eulerov krug je staza koja prolazi svaki rub grafa točno jednom i staza završava na početnom vrhu.
Bilješka: Zadani graf sadrži Eulerov krug.
Primjer:
Ulaz: usmjereni graf

Izlaz: 0 3 4 0 2 1 0
Preduvjeti:
- Razgovarali smo o problem otkrivanja je li dati graf Eulerov ili nije za neusmjereni graf
- Uvjeti za Eulerov krug u usmjerenom grpagu: (1) Svi vrhovi pripadaju jednoj jako povezanoj komponenti. (2) Svi vrhovi imaju isti ulazni i izlazni stupanj. Imajte na umu da je za neusmjereni graf uvjet drugačiji (svi vrhovi imaju paran stupanj)
Pristup:
- Odaberite bilo koji početni vrh v i slijedite trag bridova od tog vrha do povratka u v. Nije moguće zapeti ni na jednom vrhu osim v jer indegree i outdegree svakog vrha moraju biti isti kada trag uđe u drugi vrh w mora postojati neiskorišten brid koji izlazi iz w. Ovako formirana tura je zatvorena tura ali možda neće pokriti sve vrhove i bridove početnog grafa.
- Sve dok postoji vrh u koji pripada trenutnom obilasku, ali ima susjedne bridove koji nisu dio obilaska, započnite drugi trag od u prateći neiskorištene bridove do povratka na u i pridružite tako formirani obilazak prethodnom obilasku.
Ilustracija:
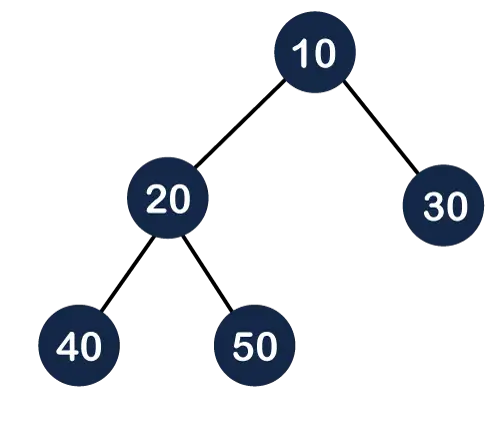
Uzimamo primjer gornjeg grafikona s 5 čvorova: adj = {{2 3} {0} {1} {4} {0}}.
- Počnite od vrha 0 :
- Trenutni put: [0]
- Krug: []
- Vrh 0 → 3 :
- Trenutni put: [0 3]
- Krug: []
- Verteks 3 → 4 :
- Trenutni put: [0 3 4]
- Krug: []
- Vrh 4 → 0 :
- Trenutni put: [0 3 4 0]
- Krug: []
- Vrh 0 → 2 :
- Trenutni put: [0 3 4 0 2]
- Krug: []
- Vrh 2 → 1 :
- Trenutni put: [0 3 4 0 2 1]
- Krug: []
- Vrh 1 → 0 :
- Trenutni put: [0 3 4 0 2 1 0]
- Krug: []
- Povratak do vrha 0 : Dodajte 0 krugu.
- Trenutni put: [0 3 4 0 2 1]
- Krug: [0]
- Povratak do vrha 1 : Dodajte 1 krugu.
- Trenutni put: [0 3 4 0 2]
- Krug: [0 1]
- Povratak do vrha 2 : Dodajte 2 krugu.
- Trenutni put: [0 3 4 0]
- Krug: [0 1 2]
- Povratak do vrha 0 : Dodajte 0 krugu.
- Trenutni put: [0 3 4]
- Krug: [0 1 2 0]
- Povratak do vrha 4 : Dodajte 4 krugu.
- Trenutni put: [0 3]
- Krug: [0 1 2 0 4]
- Povratak do vrha 3 : Dodajte 3 krugu.
- Trenutni put: [0]
- Krug: [0 1 2 0 4 3]
- Povratak do vrha 0 : Dodajte 0 krugu.
- Trenutačni put: []
- Krug: [0 1 2 0 4 3 0]
U nastavku je implementacija gornjeg pristupa:
C++ // C++ program to print Eulerian circuit in given // directed graph using Hierholzer algorithm #include using namespace std ; // Function to print Eulerian circuit vector < int > printCircuit ( vector < vector < int >> & adj ) { int n = adj . size (); if ( n == 0 ) return {}; // Maintain a stack to keep vertices // We can start from any vertex here we start with 0 vector < int > currPath ; currPath . push_back ( 0 ); // list to store final circuit vector < int > circuit ; while ( currPath . size () > 0 ) { int currNode = currPath [ currPath . size () - 1 ]; // If there's remaining edge in adjacency list // of the current vertex if ( adj [ currNode ]. size () > 0 ) { // Find and remove the next vertex that is // adjacent to the current vertex int nextNode = adj [ currNode ]. back (); adj [ currNode ]. pop_back (); // Push the new vertex to the stack currPath . push_back ( nextNode ); } // back-track to find remaining circuit else { // Remove the current vertex and // put it in the circuit circuit . push_back ( currPath . back ()); currPath . pop_back (); } } // reverse the result vector reverse ( circuit . begin () circuit . end ()); return circuit ; } int main () { vector < vector < int >> adj = {{ 2 3 } { 0 } { 1 } { 4 } { 0 }}; vector < int > ans = printCircuit ( adj ); for ( auto v : ans ) cout < < v < < ' ' ; cout < < endl ; return 0 ; }
Java // Java program to print Eulerian circuit in given // directed graph using Hierholzer algorithm import java.util.* ; class GfG { // Function to print Eulerian circuit static List < Integer > printCircuit ( List < List < Integer >> adj ) { int n = adj . size (); if ( n == 0 ) return new ArrayList <> (); // Maintain a stack to keep vertices // We can start from any vertex here we start with 0 List < Integer > currPath = new ArrayList <> (); currPath . add ( 0 ); // list to store final circuit List < Integer > circuit = new ArrayList <> (); while ( currPath . size () > 0 ) { int currNode = currPath . get ( currPath . size () - 1 ); // If there's remaining edge in adjacency list // of the current vertex if ( adj . get ( currNode ). size () > 0 ) { // Find and remove the next vertex that is // adjacent to the current vertex int nextNode = adj . get ( currNode ). get ( adj . get ( currNode ). size () - 1 ); adj . get ( currNode ). remove ( adj . get ( currNode ). size () - 1 ); // Push the new vertex to the stack currPath . add ( nextNode ); } // back-track to find remaining circuit else { // Remove the current vertex and // put it in the circuit circuit . add ( currPath . get ( currPath . size () - 1 )); currPath . remove ( currPath . size () - 1 ); } } // reverse the result vector Collections . reverse ( circuit ); return circuit ; } public static void main ( String [] args ) { List < List < Integer >> adj = new ArrayList <> (); adj . add ( new ArrayList <> ( Arrays . asList ( 2 3 ))); adj . add ( new ArrayList <> ( Arrays . asList ( 0 ))); adj . add ( new ArrayList <> ( Arrays . asList ( 1 ))); adj . add ( new ArrayList <> ( Arrays . asList ( 4 ))); adj . add ( new ArrayList <> ( Arrays . asList ( 0 ))); List < Integer > ans = printCircuit ( adj ); for ( int v : ans ) System . out . print ( v + ' ' ); System . out . println (); } }
Python # Python program to print Eulerian circuit in given # directed graph using Hierholzer algorithm # Function to print Eulerian circuit def printCircuit ( adj ): n = len ( adj ) if n == 0 : return [] # Maintain a stack to keep vertices # We can start from any vertex here we start with 0 currPath = [ 0 ] # list to store final circuit circuit = [] while len ( currPath ) > 0 : currNode = currPath [ - 1 ] # If there's remaining edge in adjacency list # of the current vertex if len ( adj [ currNode ]) > 0 : # Find and remove the next vertex that is # adjacent to the current vertex nextNode = adj [ currNode ] . pop () # Push the new vertex to the stack currPath . append ( nextNode ) # back-track to find remaining circuit else : # Remove the current vertex and # put it in the circuit circuit . append ( currPath . pop ()) # reverse the result vector circuit . reverse () return circuit if __name__ == '__main__' : adj = [[ 2 3 ] [ 0 ] [ 1 ] [ 4 ] [ 0 ]] ans = printCircuit ( adj ) for v in ans : print ( v end = ' ' ) print ()
C# // C# program to print Eulerian circuit in given // directed graph using Hierholzer algorithm using System ; using System.Collections.Generic ; class GfG { // Function to print Eulerian circuit static List < int > printCircuit ( List < List < int >> adj ) { int n = adj . Count ; if ( n == 0 ) return new List < int > (); // Maintain a stack to keep vertices // We can start from any vertex here we start with 0 List < int > currPath = new List < int > { 0 }; // list to store final circuit List < int > circuit = new List < int > (); while ( currPath . Count > 0 ) { int currNode = currPath [ currPath . Count - 1 ]; // If there's remaining edge in adjacency list // of the current vertex if ( adj [ currNode ]. Count > 0 ) { // Find and remove the next vertex that is // adjacent to the current vertex int nextNode = adj [ currNode ][ adj [ currNode ]. Count - 1 ]; adj [ currNode ]. RemoveAt ( adj [ currNode ]. Count - 1 ); // Push the new vertex to the stack currPath . Add ( nextNode ); } // back-track to find remaining circuit else { // Remove the current vertex and // put it in the circuit circuit . Add ( currPath [ currPath . Count - 1 ]); currPath . RemoveAt ( currPath . Count - 1 ); } } // reverse the result vector circuit . Reverse (); return circuit ; } static void Main ( string [] args ) { List < List < int >> adj = new List < List < int >> { new List < int > { 2 3 } new List < int > { 0 } new List < int > { 1 } new List < int > { 4 } new List < int > { 0 } }; List < int > ans = printCircuit ( adj ); foreach ( int v in ans ) { Console . Write ( v + ' ' ); } Console . WriteLine (); } }
JavaScript // JavaScript program to print Eulerian circuit in given // directed graph using Hierholzer algorithm // Function to print Eulerian circuit function printCircuit ( adj ) { let n = adj . length ; if ( n === 0 ) return []; // Maintain a stack to keep vertices // We can start from any vertex here we start with 0 let currPath = [ 0 ]; // list to store final circuit let circuit = []; while ( currPath . length > 0 ) { let currNode = currPath [ currPath . length - 1 ]; // If there's remaining edge in adjacency list // of the current vertex if ( adj [ currNode ]. length > 0 ) { // Find and remove the next vertex that is // adjacent to the current vertex let nextNode = adj [ currNode ]. pop (); // Push the new vertex to the stack currPath . push ( nextNode ); } // back-track to find remaining circuit else { // Remove the current vertex and // put it in the circuit circuit . push ( currPath . pop ()); } } // reverse the result vector circuit . reverse (); return circuit ; } let adj = [[ 2 3 ] [ 0 ] [ 1 ] [ 4 ] [ 0 ]]; let ans = printCircuit ( adj ); for ( let v of ans ) { console . log ( v ' ' ); }
Izlaz
0 3 4 0 2 1 0
Vremenska složenost: O(V + E) gdje je V broj vrhova, a E broj bridova u grafu. Razlog za to je taj što algoritam izvodi dubinsko pretraživanje (DFS) i posjećuje svaki vrh i svaki rub točno jednom. Dakle, za svaki vrh je potrebno O(1) vremena da ga se obiđe i za svaki brid je potrebno O(1) vremena da ga se obiđe.
Složenost prostora : O(V + E) kao algoritam koristi stog za pohranjivanje trenutne putanje i popis za pohranjivanje konačnog kruga. Maksimalna veličina hrpe može biti V + E u najgorem slučaju, tako da je složenost prostora O(V + E).
Napravi kviz