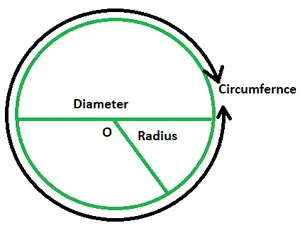
Ympyrä koostuu pisteistä, jotka ovat kaikki samalla etäisyydellä ympyrän keskustasta. Suljettu geometrinen muoto on ympyrä. Arkielämässä näemme ympyröitä pyörän, pizzan, pyöreän maan ja niin edelleen muodossa.

Ympyrän osat

Avainkäsitteet:

• Säde: The ympyrän säde on sen keskustan ja minkä tahansa reunan pisteen välinen etäisyys. Se on yleensä merkitty r:llä. Ympyrällä on loputon määrä säteitä.
• Halkaisija: Se on viiva, joka kulkee keskustan läpi ja jonka päät ovat ympyrässä. Sitä merkitään D:llä ja se on kaksi kertaa ympyrän säteen arvo.
• Ympärysmitta: Ympyrän reunuksen laajuus on yhtä suuri kuin sen ympärysmitta. Tämä tarkoittaa, että ympyrän kehä on yhtä suuri kuin sen ympärysmitta. Ympyrän ympärysmitta on yhtä suuri kuin sen kehän ympärille siististi kiertyneen langan pituus. Se annetaan muodossa 2πr.

Mikä on ympyrän alue?

Ympyrän pinta-ala liittyy ympyrän reunan peittämän tilan määrään. Ympyrän täyttämä alue on ympyrän kehällä oleva alue. Se tunnetaan myös ympyrään sisältyvien neliöyksiköiden kokonaismääränä.

Tarkistaa: Ympyrän halkaisija

Ympyräkaavojen alue

Ympyrän pinta-ala saadaan seuraavalla kaavalla:

A = πr ²

missä r on annetun ympyrän säde.

tai

A = C ² /4s

missä C on annetun ympyrän ympärysmitta.

Esimerkkejä ympyräkaavan alueesta

Tehtävä 1. Etsi ympyrän pinta-ala, kun sen säde on 8 m.

Ratkaisu:

Annettu: r = 8 m

Koska ympyrän pinta-ala = πr ²

A = π(8) ²

= 64 p

= 200,96 m ²

Kysymys 2. Etsi ympyrän pinta-ala, kun sen ympärysmitta on 12 cm.

Ratkaisu:

Annettu: C = 12 cm

Koska A = C ² /4s

= 12 ² /4s

= 11,46 cm ²

Kysymys 3. Etsi ympyrän pinta-ala, kun sen halkaisija on 12 cm.

Ratkaisu:

Annettu: D = 12 cm

tai säde = r = 12/2 = 6 cm

Koska A = πr ²

= π(6)2

= 113,04 cm ²

Tehtävä 4. Etsi ympyrän pinta-ala, kun sen säde on 9 cm.

Ratkaisu:

Annettu: r = 9 m

Koska ympyrän pinta-ala = πr ²

A = π(9) ²

= 81 p

= 254,34 cm ²

Kysymys 5. Etsi ympyrän pinta-ala, kun sen halkaisija on 10 cm.

Ratkaisu:

Annettu: D = 10 cm

tai säde = r = 10/2 = 5 cm

Koska A = πr ²

= π(5) ²

= 78,5 cm ²

Tarkista myös:

• Ympyrän alueen laskin
• Square Footage of Circle Calculator
• Ympyrän säde Laskin
• Halkaisija Ympyrä Laskin
• Ympärysmitan laskin
• Ympärysmitta halkaisijalaskuriin