Laske maksimipisteet samalla rivillä


Annettaessa n pistettä 2D-tasolla (x y)-koordinaattien parina meidän on löydettävä suurin määrä pisteitä, jotka sijaitsevat samalla suoralla.
Esimerkkejä:
Syöte : pisteet[] = {-1 1} {0 0} {1 1}
{2 2} {3 3} {3 4}
Lähtö : 4
Sitten suurin määrä pisteitä, jotka sijaitsevat samalla tasolla
rivit ovat 4, ne pisteet ovat {0 0} {1 1} {2 2}
{3 3}
Laske jokaiselle pisteelle p sen kaltevuus muiden pisteiden kanssa ja käytä karttaa kirjaamaan kuinka monella pisteellä on sama kaltevuus, jonka avulla voimme selvittää, kuinka monta pistettä on samalla suoralla, jossa p on niiden yksi piste. Tee jokaiselle pisteelle sama asia ja päivitä tähän mennessä löydetty enimmäispistemäärä.
Toteutuksessa on otettava huomioon seuraavat asiat:
- jos kaksi pistettä ovat (x1 y1) ja (x2 y2), niin niiden kaltevuus on (y2 – y1) / (x2 – x1), mikä voi olla kaksinkertainen arvo ja voi aiheuttaa tarkkuusongelmia. Päästäksemme eroon tarkkuusongelmista käsittelemme kaltevuutta parina ((y2 - y1) (x2 - x1)) suhteen sijaan ja pienennämme paria niiden gcd:llä ennen lisäämistä karttaan. Alla olevassa koodissa pystysuorat tai toistuvat kohdat käsitellään erikseen.
- Jos käytämme kaltevuusparin tallentamiseen Hash Map tai Dictionary, niin ratkaisun kokonaisaikakompleksisuus on O(n^2) ja avaruuden kompleksisuus on O(n).
/* C/C++ program to find maximum number of point which lie on same line */ #include #include using namespace std ; // method to find maximum collinear point int maxPointOnSameLine ( vector < pair < int int > > points ) { int N = points . size (); if ( N < 2 ) return N ; int maxPoint = 0 ; int curMax overlapPoints verticalPoints ; // here since we are using unordered_map // which is based on hash function //But by default we don't have hash function for pairs //so we'll use hash function defined in Boost library unordered_map < pair < int int > int boost :: hash < pair < int int > > > slopeMap ; // looping for each point for ( int i = 0 ; i < N ; i ++ ) { curMax = overlapPoints = verticalPoints = 0 ; // looping from i + 1 to ignore same pair again for ( int j = i + 1 ; j < N ; j ++ ) { // If both point are equal then just // increase overlapPoint count if ( points [ i ] == points [ j ]) overlapPoints ++ ; // If x co-ordinate is same then both // point are vertical to each other else if ( points [ i ]. first == points [ j ]. first ) verticalPoints ++ ; else { int yDif = points [ j ]. second - points [ i ]. second ; int xDif = points [ j ]. first - points [ i ]. first ; int g = __gcd ( xDif yDif ); // reducing the difference by their gcd yDif /= g ; xDif /= g ; // increasing the frequency of current slope // in map slopeMap [ make_pair ( yDif xDif )] ++ ; curMax = max ( curMax slopeMap [ make_pair ( yDif xDif )]); } curMax = max ( curMax verticalPoints ); } // updating global maximum by current point's maximum maxPoint = max ( maxPoint curMax + overlapPoints + 1 ); // printf('maximum collinear point // which contains current point // are : %dn' curMax + overlapPoints + 1); slopeMap . clear (); } return maxPoint ; } // Driver code int main () { const int N = 6 ; int arr [ N ][ 2 ] = {{ -1 1 } { 0 0 } { 1 1 } { 2 2 } { 3 3 } { 3 4 }}; vector < pair < int int > > points ; for ( int i = 0 ; i < N ; i ++ ) points . push_back ( make_pair ( arr [ i ][ 0 ] arr [ i ][ 1 ])); cout < < maxPointOnSameLine ( points ) < < endl ; return 0 ; }
Java /* Java program to find maximum number of point which lie on same line */ import java.util.* ; class GFG { static int gcd ( int p int q ) { if ( q == 0 ) { return p ; } int r = p % q ; return gcd ( q r ); } static int N = 6 ; // method to find maximum collinear point static int maxPointOnSameLine ( int [][] points ) { if ( N < 2 ) return N ; int maxPoint = 0 ; int curMax overlapPoints verticalPoints ; HashMap < String Integer > slopeMap = new HashMap <> (); // looping for each point for ( int i = 0 ; i < N ; i ++ ) { curMax = overlapPoints = verticalPoints = 0 ; // looping from i + 1 to ignore same pair again for ( int j = i + 1 ; j < N ; j ++ ) { // If both point are equal then just // increase overlapPoint count if ( points [ i ][ 0 ] == points [ j ][ 0 ] && points [ i ][ 1 ] == points [ j ][ 1 ] ) overlapPoints ++ ; // If x co-ordinate is same then both // point are vertical to each other else if ( points [ i ][ 0 ] == points [ j ][ 0 ] ) verticalPoints ++ ; else { int yDif = points [ j ][ 1 ] - points [ i ][ 1 ] ; int xDif = points [ j ][ 0 ] - points [ i ][ 0 ] ; int g = gcd ( xDif yDif ); // reducing the difference by their gcd yDif /= g ; xDif /= g ; // Convert the pair into a string to use // as dictionary key String pair = ( yDif ) + ' ' + ( xDif ); if ( ! slopeMap . containsKey ( pair )) slopeMap . put ( pair 0 ); // increasing the frequency of current // slope in map slopeMap . put ( pair slopeMap . get ( pair ) + 1 ); curMax = Math . max ( curMax slopeMap . get ( pair )); } curMax = Math . max ( curMax verticalPoints ); } // updating global maximum by current point's // maximum maxPoint = Math . max ( maxPoint curMax + overlapPoints + 1 ); slopeMap . clear (); } return maxPoint ; } public static void main ( String [] args ) { int points [][] = { { - 1 1 } { 0 0 } { 1 1 } { 2 2 } { 3 3 } { 3 4 } }; System . out . println ( maxPointOnSameLine ( points )); } }
Python # python3 program to find maximum number of 2D points that lie on the same line. from collections import defaultdict from math import gcd from typing import DefaultDict List Tuple IntPair = Tuple [ int int ] def normalized_slope ( a : IntPair b : IntPair ) -> IntPair : ''' Returns normalized (rise run) tuple. We won't return the actual rise/run result in order to avoid floating point math which leads to faulty comparisons. See https://en.wikipedia.org/wiki/Floating-point_arithmetic#Accuracy_problems ''' run = b [ 0 ] - a [ 0 ] # normalize undefined slopes to (1 0) if run == 0 : return ( 1 0 ) # normalize to left-to-right if run < 0 : a b = b a run = b [ 0 ] - a [ 0 ] rise = b [ 1 ] - a [ 1 ] # Normalize by greatest common divisor. # math.gcd only works on positive numbers. gcd_ = gcd ( abs ( rise ) run ) return ( rise // gcd_ run // gcd_ ) def maximum_points_on_same_line ( points : List [ List [ int ]]) -> int : # You need at least 3 points to potentially have non-collinear points. # For [0 2] points all points are on the same line. if len ( points ) < 3 : return len ( points ) # Note that every line we find will have at least 2 points. # There will be at least one line because len(points) >= 3. # Therefore it's safe to initialize to 0. max_val = 0 for a_index in range ( 0 len ( points ) - 1 ): # All lines in this iteration go through point a. # Note that lines a-b and a-c cannot be parallel. # Therefore if lines a-b and a-c have the same slope they're the same # line. a = tuple ( points [ a_index ]) # Fresh lines already have a so default=1 slope_counts : DefaultDict [ IntPair int ] = defaultdict ( lambda : 1 ) for b_index in range ( a_index + 1 len ( points )): b = tuple ( points [ b_index ]) slope_counts [ normalized_slope ( a b )] += 1 max_val = max ( max_val max ( slope_counts . values ()) ) return max_val print ( maximum_points_on_same_line ([ [ - 1 1 ] [ 0 0 ] [ 1 1 ] [ 2 2 ] [ 3 3 ] [ 3 4 ] ])) # This code is contributed by Jose Alvarado Torre
C# /* C# program to find maximum number of point which lie on same line */ using System ; using System.Collections.Generic ; class GFG { static int gcd ( int p int q ) { if ( q == 0 ) { return p ; } int r = p % q ; return gcd ( q r ); } static int N = 6 ; // method to find maximum collinear point static int maxPointOnSameLine ( int [ ] points ) { if ( N < 2 ) return N ; int maxPoint = 0 ; int curMax overlapPoints verticalPoints ; Dictionary < string int > slopeMap = new Dictionary < string int > (); // looping for each point for ( int i = 0 ; i < N ; i ++ ) { curMax = overlapPoints = verticalPoints = 0 ; // looping from i + 1 to ignore same pair again for ( int j = i + 1 ; j < N ; j ++ ) { // If both point are equal then just // increase overlapPoint count if ( points [ i 0 ] == points [ j 0 ] && points [ i 1 ] == points [ j 1 ]) overlapPoints ++ ; // If x co-ordinate is same then both // point are vertical to each other else if ( points [ i 0 ] == points [ j 0 ]) verticalPoints ++ ; else { int yDif = points [ j 1 ] - points [ i 1 ]; int xDif = points [ j 0 ] - points [ i 0 ]; int g = gcd ( xDif yDif ); // reducing the difference by their gcd yDif /= g ; xDif /= g ; // Convert the pair into a string to use // as dictionary key string pair = Convert . ToString ( yDif ) + ' ' + Convert . ToString ( xDif ); if ( ! slopeMap . ContainsKey ( pair )) slopeMap [ pair ] = 0 ; // increasing the frequency of current // slope in map slopeMap [ pair ] ++ ; curMax = Math . Max ( curMax slopeMap [ pair ]); } curMax = Math . Max ( curMax verticalPoints ); } // updating global maximum by current point's // maximum maxPoint = Math . Max ( maxPoint curMax + overlapPoints + 1 ); slopeMap . Clear (); } return maxPoint ; } // Driver code public static void Main ( string [] args ) { int [ ] points = { { - 1 1 } { 0 0 } { 1 1 } { 2 2 } { 3 3 } { 3 4 } }; Console . WriteLine ( maxPointOnSameLine ( points )); } } // This code is contributed by phasing17
JavaScript /* JavaScript program to find maximum number of point which lie on same line */ // Function to find gcd of two numbers let gcd = function ( a b ) { if ( ! b ) { return a ; } return gcd ( b a % b ); } // method to find maximum collinear point function maxPointOnSameLine ( points ){ let N = points . length ; if ( N < 2 ){ return N ; } let maxPoint = 0 ; let curMax overlapPoints verticalPoints ; // Creating a map for storing the data. let slopeMap = new Map (); // looping for each point for ( let i = 0 ; i < N ; i ++ ) { curMax = 0 ; overlapPoints = 0 ; verticalPoints = 0 ; // looping from i + 1 to ignore same pair again for ( let j = i + 1 ; j < N ; j ++ ) { // If both point are equal then just // increase overlapPoint count if ( points [ i ] === points [ j ]){ overlapPoints ++ ; } // If x co-ordinate is same then both // point are vertical to each other else if ( points [ i ][ 0 ] === points [ j ][ 0 ]){ verticalPoints ++ ; } else { let yDif = points [ j ][ 1 ] - points [ i ][ 1 ]; let xDif = points [ j ][ 0 ] - points [ i ][ 0 ]; let g = gcd ( xDif yDif ); // reducing the difference by their gcd yDif = Math . floor ( yDif / g ); xDif = Math . floor ( xDif / g ); // increasing the frequency of current slope. let tmp = [ yDif xDif ]; if ( slopeMap . has ( tmp . join ( '' ))){ slopeMap . set ( tmp . join ( '' ) slopeMap . get ( tmp . join ( '' )) + 1 ); } else { slopeMap . set ( tmp . join ( '' ) 1 ); } curMax = Math . max ( curMax slopeMap . get ( tmp . join ( '' ))); } curMax = Math . max ( curMax verticalPoints ); } // updating global maximum by current point's maximum maxPoint = Math . max ( maxPoint curMax + overlapPoints + 1 ); // printf('maximum collinear point // which contains current point // are : %dn' curMax + overlapPoints + 1); slopeMap . clear (); } return maxPoint ; } // Driver code { let N = 6 ; let arr = [[ - 1 1 ] [ 0 0 ] [ 1 1 ] [ 2 2 ] [ 3 3 ] [ 3 4 ]]; console . log ( maxPointOnSameLine ( arr )); } // The code is contributed by Gautam goel (gautamgoel962)
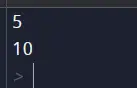
Lähtö
4
Aika monimutkaisuus: O(n 2 rauhallinen) missä n tarkoittaa merkkijonon pituutta.
Aputila: O(n)