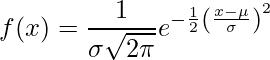Búsqueda por interpolación
Dada una matriz ordenada de n valores distribuidos uniformemente arr[] escriba una función para buscar un elemento particular x en la matriz.
La búsqueda lineal encuentra el elemento en tiempo O(n) Saltar búsqueda toma O(n) tiempo y Búsqueda binaria toma tiempo O (log n).
La búsqueda por interpolación es una mejora con respecto a Búsqueda binaria para casos en los que los valores de una matriz ordenada se distribuyen uniformemente. La interpolación construye nuevos puntos de datos dentro del rango de un conjunto discreto de puntos de datos conocidos. La búsqueda binaria siempre va al elemento central para comprobarlo. Por otro lado, la búsqueda por interpolación puede ir a diferentes ubicaciones según el valor de la clave que se busca. Por ejemplo, si el valor de la clave está más cerca del último elemento, es probable que la búsqueda por interpolación comience hacia el lado final.
Para encontrar la posición a buscar se utiliza la siguiente fórmula.
// La idea de la fórmula es devolver un valor más alto de pos
// cuando el elemento a buscar está más cerca de arr[hi]. Y
// valor más pequeño cuando está más cerca de arr[lo]arr[] ==> Matriz donde se deben buscar los elementos
x ==> Elemento a buscar
lo ==> Índice inicial en arr[]
hola ==> Índice final en arr[]
después = el +
Existen muchos métodos de interpolación diferentes y uno de ellos se conoce como interpolación lineal. La interpolación lineal toma dos puntos de datos que asumimos como (x1y1) y (x2y2) y la fórmula es: en el punto (xy).
Este algoritmo funciona de la misma manera que buscamos una palabra en un diccionario. El algoritmo de búsqueda por interpolación mejora el algoritmo de búsqueda binaria. La fórmula para encontrar un valor es: K = > K es una constante que se utiliza para reducir el espacio de búsqueda. En el caso de la búsqueda binaria el valor de esta constante es: K=(bajo+alto)/2.
La fórmula para pos se puede derivar de la siguiente manera.
Let's assume that the elements of the array are linearly distributed.
General equation of line : y = m*x + c.
y is the value in the array and x is its index.
Now putting value of lohi and x in the equation
arr[hi] = m*hi+c ----(1)
arr[lo] = m*lo+c ----(2)
x = m*pos + c ----(3)
m = (arr[hi] - arr[lo] )/ (hi - lo)
subtracting eqxn (2) from (3)
x - arr[lo] = m * (pos - lo)
lo + (x - arr[lo])/m = pos
pos = lo + (x - arr[lo]) *(hi - lo)/(arr[hi] - arr[lo])Algoritmo
El resto del algoritmo de interpolación es el mismo excepto por la lógica de partición anterior.
- Paso 1: En un bucle, calcule el valor de 'pos' usando la fórmula de posición de la sonda.
- Paso 2: Si coincide, devuelva el índice del elemento y salga.
- Paso 3: Si el elemento es menor que arr[pos], calcule la posición de la sonda del subconjunto izquierdo. De lo contrario, calcule lo mismo en el subconjunto derecho.
- Paso 4: Repita hasta que se encuentre una coincidencia o la submatriz se reduzca a cero.
A continuación se muestra la implementación del algoritmo.
// C++ program to implement interpolation // search with recursion #include using namespace std ; // If x is present in arr[0..n-1] then returns // index of it else returns -1. int interpolationSearch ( int arr [] int lo int hi int x ) { int pos ; // Since array is sorted an element present // in array must be in range defined by corner if ( lo <= hi && x >= arr [ lo ] && x <= arr [ hi ]) { // Probing the position with keeping // uniform distribution in mind. pos = lo + ((( double )( hi - lo ) / ( arr [ hi ] - arr [ lo ])) * ( x - arr [ lo ])); // Condition of target found if ( arr [ pos ] == x ) return pos ; // If x is larger x is in right sub array if ( arr [ pos ] < x ) return interpolationSearch ( arr pos + 1 hi x ); // If x is smaller x is in left sub array if ( arr [ pos ] > x ) return interpolationSearch ( arr lo pos - 1 x ); } return -1 ; } // Driver Code int main () { // Array of items on which search will // be conducted. int arr [] = { 10 12 13 16 18 19 20 21 22 23 24 33 35 42 47 }; int n = sizeof ( arr ) / sizeof ( arr [ 0 ]); // Element to be searched int x = 18 ; int index = interpolationSearch ( arr 0 n - 1 x ); // If element was found if ( index != -1 ) cout < < 'Element found at index ' < < index ; else cout < < 'Element not found.' ; return 0 ; } // This code is contributed by equbalzeeshan
C // C program to implement interpolation search // with recursion #include // If x is present in arr[0..n-1] then returns // index of it else returns -1. int interpolationSearch ( int arr [] int lo int hi int x ) { int pos ; // Since array is sorted an element present // in array must be in range defined by corner if ( lo <= hi && x >= arr [ lo ] && x <= arr [ hi ]) { // Probing the position with keeping // uniform distribution in mind. pos = lo + ((( double )( hi - lo ) / ( arr [ hi ] - arr [ lo ])) * ( x - arr [ lo ])); // Condition of target found if ( arr [ pos ] == x ) return pos ; // If x is larger x is in right sub array if ( arr [ pos ] < x ) return interpolationSearch ( arr pos + 1 hi x ); // If x is smaller x is in left sub array if ( arr [ pos ] > x ) return interpolationSearch ( arr lo pos - 1 x ); } return -1 ; } // Driver Code int main () { // Array of items on which search will // be conducted. int arr [] = { 10 12 13 16 18 19 20 21 22 23 24 33 35 42 47 }; int n = sizeof ( arr ) / sizeof ( arr [ 0 ]); int x = 18 ; // Element to be searched int index = interpolationSearch ( arr 0 n - 1 x ); // If element was found if ( index != -1 ) printf ( 'Element found at index %d' index ); else printf ( 'Element not found.' ); return 0 ; }
Java // Java program to implement interpolation // search with recursion import java.util.* ; class GFG { // If x is present in arr[0..n-1] then returns // index of it else returns -1. public static int interpolationSearch ( int arr [] int lo int hi int x ) { int pos ; // Since array is sorted an element // present in array must be in range // defined by corner if ( lo <= hi && x >= arr [ lo ] && x <= arr [ hi ] ) { // Probing the position with keeping // uniform distribution in mind. pos = lo + ((( hi - lo ) / ( arr [ hi ] - arr [ lo ] )) * ( x - arr [ lo ] )); // Condition of target found if ( arr [ pos ] == x ) return pos ; // If x is larger x is in right sub array if ( arr [ pos ] < x ) return interpolationSearch ( arr pos + 1 hi x ); // If x is smaller x is in left sub array if ( arr [ pos ] > x ) return interpolationSearch ( arr lo pos - 1 x ); } return - 1 ; } // Driver Code public static void main ( String [] args ) { // Array of items on which search will // be conducted. int arr [] = { 10 12 13 16 18 19 20 21 22 23 24 33 35 42 47 }; int n = arr . length ; // Element to be searched int x = 18 ; int index = interpolationSearch ( arr 0 n - 1 x ); // If element was found if ( index != - 1 ) System . out . println ( 'Element found at index ' + index ); else System . out . println ( 'Element not found.' ); } } // This code is contributed by equbalzeeshan
Python # Python3 program to implement # interpolation search # with recursion # If x is present in arr[0..n-1] then # returns index of it else returns -1. def interpolationSearch ( arr lo hi x ): # Since array is sorted an element present # in array must be in range defined by corner if ( lo <= hi and x >= arr [ lo ] and x <= arr [ hi ]): # Probing the position with keeping # uniform distribution in mind. pos = lo + (( hi - lo ) // ( arr [ hi ] - arr [ lo ]) * ( x - arr [ lo ])) # Condition of target found if arr [ pos ] == x : return pos # If x is larger x is in right subarray if arr [ pos ] < x : return interpolationSearch ( arr pos + 1 hi x ) # If x is smaller x is in left subarray if arr [ pos ] > x : return interpolationSearch ( arr lo pos - 1 x ) return - 1 # Driver code # Array of items in which # search will be conducted arr = [ 10 12 13 16 18 19 20 21 22 23 24 33 35 42 47 ] n = len ( arr ) # Element to be searched x = 18 index = interpolationSearch ( arr 0 n - 1 x ) if index != - 1 : print ( 'Element found at index' index ) else : print ( 'Element not found' ) # This code is contributed by Hardik Jain
C# // C# program to implement // interpolation search using System ; class GFG { // If x is present in // arr[0..n-1] then // returns index of it // else returns -1. static int interpolationSearch ( int [] arr int lo int hi int x ) { int pos ; // Since array is sorted an element // present in array must be in range // defined by corner if ( lo <= hi && x >= arr [ lo ] && x <= arr [ hi ]) { // Probing the position // with keeping uniform // distribution in mind. pos = lo + ((( hi - lo ) / ( arr [ hi ] - arr [ lo ])) * ( x - arr [ lo ])); // Condition of // target found if ( arr [ pos ] == x ) return pos ; // If x is larger x is in right sub array if ( arr [ pos ] < x ) return interpolationSearch ( arr pos + 1 hi x ); // If x is smaller x is in left sub array if ( arr [ pos ] > x ) return interpolationSearch ( arr lo pos - 1 x ); } return - 1 ; } // Driver Code public static void Main () { // Array of items on which search will // be conducted. int [] arr = new int []{ 10 12 13 16 18 19 20 21 22 23 24 33 35 42 47 }; // Element to be searched int x = 18 ; int n = arr . Length ; int index = interpolationSearch ( arr 0 n - 1 x ); // If element was found if ( index != - 1 ) Console . WriteLine ( 'Element found at index ' + index ); else Console . WriteLine ( 'Element not found.' ); } } // This code is contributed by equbalzeeshan
JavaScript < script > // Javascript program to implement Interpolation Search // If x is present in arr[0..n-1] then returns // index of it else returns -1. function interpolationSearch ( arr lo hi x ){ let pos ; // Since array is sorted an element present // in array must be in range defined by corner if ( lo <= hi && x >= arr [ lo ] && x <= arr [ hi ]) { // Probing the position with keeping // uniform distribution in mind. pos = lo + Math . floor ((( hi - lo ) / ( arr [ hi ] - arr [ lo ])) * ( x - arr [ lo ]));; // Condition of target found if ( arr [ pos ] == x ){ return pos ; } // If x is larger x is in right sub array if ( arr [ pos ] < x ){ return interpolationSearch ( arr pos + 1 hi x ); } // If x is smaller x is in left sub array if ( arr [ pos ] > x ){ return interpolationSearch ( arr lo pos - 1 x ); } } return - 1 ; } // Driver Code let arr = [ 10 12 13 16 18 19 20 21 22 23 24 33 35 42 47 ]; let n = arr . length ; // Element to be searched let x = 18 let index = interpolationSearch ( arr 0 n - 1 x ); // If element was found if ( index != - 1 ){ document . write ( `Element found at index ${ index } ` ) } else { document . write ( 'Element not found' ); } // This code is contributed by _saurabh_jaiswal < /script>
PHP // PHP program to implement $erpolation search // with recursion // If x is present in arr[0..n-1] then returns // index of it else returns -1. function interpolationSearch ( $arr $lo $hi $x ) { // Since array is sorted an element present // in array must be in range defined by corner if ( $lo <= $hi && $x >= $arr [ $lo ] && $x <= $arr [ $hi ]) { // Probing the position with keeping // uniform distribution in mind. $pos = ( int )( $lo + ((( double )( $hi - $lo ) / ( $arr [ $hi ] - $arr [ $lo ])) * ( $x - $arr [ $lo ]))); // Condition of target found if ( $arr [ $pos ] == $x ) return $pos ; // If x is larger x is in right sub array if ( $arr [ $pos ] < $x ) return interpolationSearch ( $arr $pos + 1 $hi $x ); // If x is smaller x is in left sub array if ( $arr [ $pos ] > $x ) return interpolationSearch ( $arr $lo $pos - 1 $x ); } return - 1 ; } // Driver Code // Array of items on which search will // be conducted. $arr = array ( 10 12 13 16 18 19 20 21 22 23 24 33 35 42 47 ); $n = sizeof ( $arr ); $x = 47 ; // Element to be searched $index = interpolationSearch ( $arr 0 $n - 1 $x ); // If element was found if ( $index != - 1 ) echo 'Element found at index ' . $index ; else echo 'Element not found.' ; return 0 ; #This code is contributed by Susobhan Akhuli ?>
Producción
Element found at index 4
Complejidad del tiempo: O(registro 2 (registro 2 n)) para el caso promedio y O(n) para el peor caso
Complejidad del espacio auxiliar: O(1)
Otro enfoque: -
Este es el enfoque de iteración para la búsqueda por interpolación.
- Paso 1: En un bucle, calcule el valor de 'pos' usando la fórmula de posición de la sonda.
- Paso 2: Si coincide, devuelva el índice del elemento y salga.
- Paso 3: Si el elemento es menor que arr[pos], calcule la posición de la sonda del subconjunto izquierdo. De lo contrario, calcule lo mismo en el subconjunto derecho.
- Paso 4: Repita hasta que se encuentre una coincidencia o la submatriz se reduzca a cero.
A continuación se muestra la implementación del algoritmo.
C++ // C++ program to implement interpolation search by using iteration approach #include using namespace std ; int interpolationSearch ( int arr [] int n int x ) { // Find indexes of two corners int low = 0 high = ( n - 1 ); // Since array is sorted an element present // in array must be in range defined by corner while ( low <= high && x >= arr [ low ] && x <= arr [ high ]) { if ( low == high ) { if ( arr [ low ] == x ) return low ; return -1 ; } // Probing the position with keeping // uniform distribution in mind. int pos = low + ((( double )( high - low ) / ( arr [ high ] - arr [ low ])) * ( x - arr [ low ])); // Condition of target found if ( arr [ pos ] == x ) return pos ; // If x is larger x is in upper part if ( arr [ pos ] < x ) low = pos + 1 ; // If x is smaller x is in the lower part else high = pos - 1 ; } return -1 ; } // Main function int main () { // Array of items on whighch search will // be conducted. int arr [] = { 10 12 13 16 18 19 20 21 22 23 24 33 35 42 47 }; int n = sizeof ( arr ) / sizeof ( arr [ 0 ]); int x = 18 ; // Element to be searched int index = interpolationSearch ( arr n x ); // If element was found if ( index != -1 ) cout < < 'Element found at index ' < < index ; else cout < < 'Element not found.' ; return 0 ; } //this code contributed by Ajay Singh
Java // Java program to implement interpolation // search with recursion import java.util.* ; class GFG { // If x is present in arr[0..n-1] then returns // index of it else returns -1. public static int interpolationSearch ( int arr [] int lo int hi int x ) { int pos ; if ( lo <= hi && x >= arr [ lo ] && x <= arr [ hi ] ) { // Probing the position with keeping // uniform distribution in mind. pos = lo + ((( hi - lo ) / ( arr [ hi ] - arr [ lo ] )) * ( x - arr [ lo ] )); // Condition of target found if ( arr [ pos ] == x ) return pos ; // If x is larger x is in right sub array if ( arr [ pos ] < x ) return interpolationSearch ( arr pos + 1 hi x ); // If x is smaller x is in left sub array if ( arr [ pos ] > x ) return interpolationSearch ( arr lo pos - 1 x ); } return - 1 ; } // Driver Code public static void main ( String [] args ) { // Array of items on which search will // be conducted. int arr [] = { 10 12 13 16 18 19 20 21 22 23 24 33 35 42 47 }; int n = arr . length ; // Element to be searched int x = 18 ; int index = interpolationSearch ( arr 0 n - 1 x ); // If element was found if ( index != - 1 ) System . out . println ( 'Element found at index ' + index ); else System . out . println ( 'Element not found.' ); } }
Python # Python equivalent of above C++ code # Python program to implement interpolation search by using iteration approach def interpolationSearch ( arr n x ): # Find indexes of two corners low = 0 high = ( n - 1 ) # Since array is sorted an element present # in array must be in range defined by corner while low <= high and x >= arr [ low ] and x <= arr [ high ]: if low == high : if arr [ low ] == x : return low ; return - 1 ; # Probing the position with keeping # uniform distribution in mind. pos = int ( low + ((( float ( high - low ) / ( arr [ high ] - arr [ low ])) * ( x - arr [ low ])))) # Condition of target found if arr [ pos ] == x : return pos # If x is larger x is in upper part if arr [ pos ] < x : low = pos + 1 ; # If x is smaller x is in lower part else : high = pos - 1 ; return - 1 # Main function if __name__ == '__main__' : # Array of items on whighch search will # be conducted. arr = [ 10 12 13 16 18 19 20 21 22 23 24 33 35 42 47 ] n = len ( arr ) x = 18 # Element to be searched index = interpolationSearch ( arr n x ) # If element was found if index != - 1 : print ( 'Element found at index' index ) else : print ( 'Element not found' )
C# // C# program to implement interpolation search by using // iteration approach using System ; class Program { // Interpolation Search function static int InterpolationSearch ( int [] arr int n int x ) { int low = 0 ; int high = n - 1 ; while ( low <= high && x >= arr [ low ] && x <= arr [ high ]) { if ( low == high ) { if ( arr [ low ] == x ) return low ; return - 1 ; } int pos = low + ( int )((( float )( high - low ) / ( arr [ high ] - arr [ low ])) * ( x - arr [ low ])); if ( arr [ pos ] == x ) return pos ; if ( arr [ pos ] < x ) low = pos + 1 ; else high = pos - 1 ; } return - 1 ; } // Main function static void Main ( string [] args ) { int [] arr = { 10 12 13 16 18 19 20 21 22 23 24 33 35 42 47 }; int n = arr . Length ; int x = 18 ; int index = InterpolationSearch ( arr n x ); if ( index != - 1 ) Console . WriteLine ( 'Element found at index ' + index ); else Console . WriteLine ( 'Element not found' ); } } // This code is contributed by Susobhan Akhuli
JavaScript // JavaScript program to implement interpolation search by using iteration approach function interpolationSearch ( arr n x ) { // Find indexes of two corners let low = 0 ; let high = n - 1 ; // Since array is sorted an element present // in array must be in range defined by corner while ( low <= high && x >= arr [ low ] && x <= arr [ high ]) { if ( low == high ) { if ( arr [ low ] == x ) { return low ; } return - 1 ; } // Probing the position with keeping // uniform distribution in mind. let pos = Math . floor ( low + ((( high - low ) / ( arr [ high ] - arr [ low ])) * ( x - arr [ low ]))); // Condition of target found if ( arr [ pos ] == x ) { return pos ; } // If x is larger x is in upper part if ( arr [ pos ] < x ) { low = pos + 1 ; } // If x is smaller x is in lower part else { high = pos - 1 ; } } return - 1 ; } // Main function let arr = [ 10 12 13 16 18 19 20 21 22 23 24 33 35 42 47 ]; let n = arr . length ; let x = 18 ; // Element to be searched let index = interpolationSearch ( arr n x ); // If element was found if ( index != - 1 ) { console . log ( 'Element found at index' index ); } else { console . log ( 'Element not found' ); }
Producción
Element found at index 4
Complejidad del tiempo: O(log2(log2 n)) para el caso promedio y O(n) para el peor de los casos
Complejidad del espacio auxiliar: O(1)