Dieses Tutorial ist eine anfängerfreundliche Anleitung für Lernen von Datenstrukturen und Algorithmen mit Python. In diesem Artikel besprechen wir die integrierten Datenstrukturen wie Listen, Tupel, Wörterbücher usw. sowie einige benutzerdefinierte Datenstrukturen wie z verknüpfte Listen , Bäume , Grafiken usw. und Traversal- sowie Such- und Sortieralgorithmen anhand von guten und gut erklärten Beispielen und Übungsfragen.

Listen

Python-Listen sind geordnete Datensammlungen, genau wie Arrays in anderen Programmiersprachen. Es erlaubt verschiedene Arten von Elementen in der Liste. Die Implementierung von Python List ähnelt Vectors in C++ oder ArrayList in JAVA. Der kostspielige Vorgang besteht darin, das Element am Anfang der Liste einzufügen oder zu löschen, da alle Elemente verschoben werden müssen. Auch das Einfügen und Löschen am Ende der Liste kann kostspielig werden, wenn der vorab zugewiesene Speicher voll wird.

Beispiel: Python-Liste erstellen

List = [1, 2, 3, 'GFG', 2.3] print(List) 

[1, 2, 3, 'GFG', 2.3] 

Auf Listenelemente kann über den zugewiesenen Index zugegriffen werden. In Python ist der Startindex der Liste eine Sequenz 0 und der Endindex ist (wenn N Elemente vorhanden sind) N-1.

Beispiel: Python-Listenoperationen

# Creating a List with # the use of multiple values List = ['Geeks', 'For', 'Geeks'] print('
List containing multiple values: ') print(List) # Creating a Multi-Dimensional List # (By Nesting a list inside a List) List2 = [['Geeks', 'For'], ['Geeks']] print('
Multi-Dimensional List: ') print(List2) # accessing a element from the # list using index number print('Accessing element from the list') print(List[0]) print(List[2]) # accessing a element using # negative indexing print('Accessing element using negative indexing') # print the last element of list print(List[-1]) # print the third last element of list print(List[-3]) 

List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks 

Tupel

Python-Tupel ähneln Listen, Tupel jedoch unveränderlich Es liegt in der Natur vor, d. h. wenn es einmal erstellt wurde, kann es nicht mehr verändert werden. Genau wie eine Liste kann auch ein Tupel Elemente unterschiedlichen Typs enthalten.

In Python werden Tupel erstellt, indem eine durch „Komma“ getrennte Folge von Werten mit oder ohne Verwendung von Klammern zum Gruppieren der Datenfolge platziert wird.

Notiz: Um ein Tupel aus einem Element zu erstellen, muss ein abschließendes Komma stehen. Beispielsweise erstellt (8,) ein Tupel, das 8 als Element enthält.

Beispiel: Python-Tupeloperationen

# Creating a Tuple with # the use of Strings Tuple = ('Geeks', 'For') print('
Tuple with the use of String: ') print(Tuple) # Creating a Tuple with # the use of list list1 = [1, 2, 4, 5, 6] print('
Tuple using List: ') Tuple = tuple(list1) # Accessing element using indexing print('First element of tuple') print(Tuple[0]) # Accessing element from last # negative indexing print('
Last element of tuple') print(Tuple[-1]) print('
Third last element of tuple') print(Tuple[-3]) 

Tuple with the use of String: ('Geeks', 'For') Tuple using List: First element of tuple 1 Last element of tuple 6 Third last element of tuple 4 

Satz

Python-Set ist eine veränderbare Datensammlung, die keine Duplizierung zulässt. Sets dienen im Wesentlichen dazu, die Mitgliedschaft zu testen und doppelte Einträge zu eliminieren. Die dabei verwendete Datenstruktur ist Hashing, eine beliebte Technik zum Durchführen von Einfügungen, Löschungen und Durchläufen in O(1) im Durchschnitt.

Wenn an derselben Indexposition mehrere Werte vorhanden sind, wird der Wert an diese Indexposition angehängt, um eine verknüpfte Liste zu bilden. In werden CPython-Sets mithilfe eines Wörterbuchs mit Dummy-Variablen implementiert, wobei die Schlüsselelemente die Mitglieder sind, die mit größerer Optimierung der Zeitkomplexität festgelegt werden.

Set-Implementierung:

Sets mit zahlreichen Operationen auf einer einzelnen HashTable:

Beispiel: Python-Set-Operationen

# Creating a Set with # a mixed type of values # (Having numbers and strings) Set = set([1, 2, 'Geeks', 4, 'For', 6, 'Geeks']) print('
Set with the use of Mixed Values') print(Set) # Accessing element using # for loop print('
Elements of set: ') for i in Set: print(i, end =' ') print() # Checking the element # using in keyword print('Geeks' in Set) 

Set with the use of Mixed Values {1, 2, 4, 6, 'For', 'Geeks'} Elements of set: 1 2 4 6 For Geeks True 

Gefrorene Sets

Gefrorene Sets In Python handelt es sich um unveränderliche Objekte, die nur Methoden und Operatoren unterstützen, die ein Ergebnis erzeugen, ohne die eingefrorene Menge oder Mengen zu beeinflussen, auf die sie angewendet werden. Während Elemente einer Menge jederzeit geändert werden können, bleiben Elemente der eingefrorenen Menge nach der Erstellung gleich.

Beispiel: Python Frozen-Set

# Same as {'a', 'b','c'} normal_set = set(['a', 'b','c']) print('Normal Set') print(normal_set) # A frozen set frozen_set = frozenset(['e', 'f', 'g']) print('
Frozen Set') print(frozen_set) # Uncommenting below line would cause error as # we are trying to add element to a frozen set # frozen_set.add('h') 

Normal Set {'a', 'b', 'c'} Frozen Set frozenset({'f', 'g', 'e'}) 

Zeichenfolge

Python-Strings ist das unveränderliche Array von Bytes, die Unicode-Zeichen darstellen. Python hat keinen Zeichendatentyp, ein einzelnes Zeichen ist einfach eine Zeichenfolge mit der Länge 1.

Notiz: Da Zeichenfolgen unveränderlich sind, führt die Änderung einer Zeichenfolge zur Erstellung einer neuen Kopie.

Beispiel: Python-Strings-Operationen

String = 'Welcome to GeeksForGeeks' print('Creating String: ') print(String) # Printing First character print('
First character of String is: ') print(String[0]) # Printing Last character print('
Last character of String is: ') print(String[-1]) 

Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s 

Wörterbuch

Python-Wörterbuch ist eine ungeordnete Datensammlung, die Daten im Format eines Schlüssel-Wert-Paares speichert. Es ist wie Hash-Tabellen in jeder anderen Sprache mit der zeitlichen Komplexität von O(1). Die Indizierung des Python-Wörterbuchs erfolgt mithilfe von Schlüsseln. Dabei handelt es sich um einen beliebigen hashbaren Typ, d. h. um ein Objekt, das sich nie ändern kann, wie z. B. Zeichenfolgen, Zahlen, Tupel usw. Wir können ein Wörterbuch erstellen, indem wir geschweifte Klammern ({}) oder Wörterbuchverständnis verwenden.

Beispiel: Python-Wörterbuchoperationen

# Creating a Dictionary Dict = {'Name': 'Geeks', 1: [1, 2, 3, 4]} print('Creating Dictionary: ') print(Dict) # accessing a element using key print('Accessing a element using key:') print(Dict['Name']) # accessing a element using get() # method print('Accessing a element using get:') print(Dict.get(1)) # creation using Dictionary comprehension myDict = {x: x**2 for x in [1,2,3,4,5]} print(myDict) 

Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25} 

Matrix

Eine Matrix ist ein 2D-Array, bei dem jedes Element genau die gleiche Größe hat. Um eine Matrix zu erstellen, verwenden wir die NumPy-Paket .

Beispiel: Python NumPy-Matrixoperationen

import numpy as np a = np.array([[1,2,3,4],[4,55,1,2], [8,3,20,19],[11,2,22,21]]) m = np.reshape(a,(4, 4)) print(m) # Accessing element print('
Accessing Elements') print(a[1]) print(a[2][0]) # Adding Element m = np.append(m,[[1, 15,13,11]],0) print('
Adding Element') print(m) # Deleting Element m = np.delete(m,[1],0) print('
Deleting Element') print(m) 

Ausgabe

[[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]] Accessing Elements [ 4 55 1 2] 8 Adding Element [[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] Deleting Element [[ 1 2 3 4]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] 

Bytearray

Python Bytearray liefert eine veränderbare Folge von Ganzzahlen im Bereich 0 <= x < 256.

Beispiel: Python-Bytearray-Operationen

# Creating bytearray a = bytearray((12, 8, 25, 2)) print('Creating Bytearray:') print(a) # accessing elements print('
Accessing Elements:', a[1]) # modifying elements a[1] = 3 print('
After Modifying:') print(a) # Appending elements a.append(30) print('
After Adding Elements:') print(a) 

Creating Bytearray: bytearray(b'x0cx08x19x02') Accessing Elements: 8 After Modifying: bytearray(b'x0cx03x19x02') After Adding Elements: bytearray(b'x0cx03x19x02x1e') 

Verlinkte Liste

A verlinkte Liste ist eine lineare Datenstruktur, bei der die Elemente nicht an zusammenhängenden Speicherorten gespeichert sind. Die Elemente in einer verknüpften Liste werden mithilfe von Zeigern verknüpft, wie im folgenden Bild dargestellt:

Eine verknüpfte Liste wird durch einen Zeiger auf den ersten Knoten der verknüpften Liste dargestellt. Der erste Knoten wird Kopf genannt. Wenn die verknüpfte Liste leer ist, ist der Wert des Kopfes NULL. Jeder Knoten in einer Liste besteht aus mindestens zwei Teilen:

• Daten
• Zeiger (oder Referenz) auf den nächsten Knoten

Beispiel: Definieren einer verknüpften Liste in Python

# Node class class Node: # Function to initialize the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize # next as null # Linked List class class LinkedList: # Function to initialize the Linked # List object def __init__(self): self.head = None 

Lassen Sie uns eine einfache verknüpfte Liste mit 3 Knoten erstellen.

# A simple Python program to introduce a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3)  '''  Three nodes have been created.  We have references to these three blocks as head,  second and third  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | None | | 2 | None | | 3 | None |  +----+------+ +----+------+ +----+------+  ''' llist.head.next = second; # Link first node with second  '''  Now next of first Node refers to second. So they  both are linked.  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | o-------->| 2 | null | | 3 | null |  +----+------+ +----+------+ +----+------+ ''' zweiter.nächster = dritter ; # Verknüpfen Sie den zweiten Knoten mit dem dritten Knoten ''' Jetzt bezieht sich der nächste Knoten des zweiten Knotens auf den dritten. Alle drei Knoten sind also miteinander verbunden.  llist.head zweites drittes | | |  | | |  +----+------+ +----+------+ +----+------+ | 1 | o-------->| 2 | o-------->| 3 | null |  +----+------+ +----+------+ +----+------+ ''' 

Durchquerung verknüpfter Listen

Im vorherigen Programm haben wir eine einfache verknüpfte Liste mit drei Knoten erstellt. Lassen Sie uns die erstellte Liste durchlaufen und die Daten jedes Knotens drucken. Schreiben wir zum Durchlaufen eine Allzweckfunktion printList(), die eine beliebige Liste druckt.

# A simple Python program for traversal of a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # This function prints contents of linked list # starting from head def printList(self): temp = self.head while (temp): print (temp.data) temp = temp.next # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) llist.head.next = second; # Link first node with second second.next = third; # Link second node with the third node llist.printList() 

1 2 3 

Weitere Artikel zur verlinkten Liste

• Einfügen einer verknüpften Liste
• Löschen verknüpfter Listen (Löschen eines bestimmten Schlüssels)
• Löschen verknüpfter Listen (Löschen eines Schlüssels an einer bestimmten Position)
• Länge einer verknüpften Liste ermitteln (iterativ und rekursiv)
• Durchsuchen eines Elements in einer verknüpften Liste (iterativ und rekursiv)
• N-ter Knoten vom Ende einer verknüpften Liste
• Kehren Sie eine verknüpfte Liste um

A Stapel ist eine lineare Datenstruktur, die Elemente nach dem Last-In/First-Out-Prinzip (LIFO) oder dem First-In/Last-Out-Prinzip (FILO) speichert. Im Stapel wird ein neues Element an einem Ende hinzugefügt und ein Element nur an diesem Ende entfernt. Die Einfüge- und Löschvorgänge werden oft als Push und Pop bezeichnet.

stack = [] # append() function to push # element in the stack stack.append('g') stack.append('f') stack.append('g') print('Initial stack') print(stack) # pop() function to pop # element from stack in # LIFO order print('
Elements popped from stack:') print(stack.pop()) print(stack.pop()) print(stack.pop()) print('
Stack after elements are popped:') print(stack) # uncommenting print(stack.pop()) # will cause an IndexError # as the stack is now empty 

Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: [] 

Als Stapel werden die Warteschlange ist eine lineare Datenstruktur, die Elemente nach dem FIFO-Prinzip (First In First Out) speichert. Bei einer Warteschlange wird das zuletzt hinzugefügte Element zuerst entfernt. Ein gutes Beispiel für die Warteschlange ist eine beliebige Warteschlange von Verbrauchern für eine Ressource, bei der der Verbraucher, der zuerst kam, zuerst bedient wird.

# Initializing a queue queue = [] # Adding elements to the queue queue.append('g') queue.append('f') queue.append('g') print('Initial queue') print(queue) # Removing elements from the queue print('
Elements dequeued from queue') print(queue.pop(0)) print(queue.pop(0)) print(queue.pop(0)) print('
Queue after removing elements') print(queue) # Uncommenting print(queue.pop(0)) # will raise and IndexError # as the queue is now empty 

Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements [] 

Prioritätswarteschlangen sind abstrakte Datenstrukturen, bei denen alle Daten/Werte in der Warteschlange eine bestimmte Priorität haben. Beispielsweise kommt bei Fluggesellschaften Gepäck mit der Bezeichnung Business oder First Class früher an als der Rest. Die Prioritätswarteschlange ist eine Erweiterung der Warteschlange mit den folgenden Eigenschaften.

• Ein Element mit hoher Priorität wird vor einem Element mit niedriger Priorität aus der Warteschlange entfernt.
• Wenn zwei Elemente die gleiche Priorität haben, werden sie entsprechend ihrer Reihenfolge in der Warteschlange bedient.

# A simple implementation of Priority Queue # using Queue. class PriorityQueue(object): def __init__(self): self.queue = [] def __str__(self): return ' '.join([str(i) for i in self.queue]) # for checking if the queue is empty def isEmpty(self): return len(self.queue) == 0 # for inserting an element in the queue def insert(self, data): self.queue.append(data) # for popping an element based on Priority def delete(self): try: max = 0 for i in range(len(self.queue)): if self.queue[i]>self.queue[max]: max = i item = self.queue[max] del self.queue[max] Rückgabeelement außer IndexError: print() exit() if __name__ == '__main__': myQueue = PriorityQueue( ) myQueue.insert(12) myQueue.insert(1) myQueue.insert(14) myQueue.insert(7) print(myQueue) while not myQueue.isEmpty(): print(myQueue.delete()) 

12 1 14 7 14 12 7 1 

Haufen

heapq-Modul in Python stellt die Heap-Datenstruktur bereit, die hauptsächlich zur Darstellung einer Prioritätswarteschlange verwendet wird. Die Eigenschaft dieser Datenstruktur besteht darin, dass sie immer das kleinste Element (min. Heap) zurückgibt, wenn das Element entfernt wird. Immer wenn Elemente verschoben oder entfernt werden, bleibt die Heap-Struktur erhalten. Das Element heap[0] gibt außerdem jedes Mal das kleinste Element zurück. Es unterstützt das Extrahieren und Einfügen des kleinsten Elements in den O(log n)-Zeiten.

Im Allgemeinen gibt es zwei Arten von Heaps:

• Max-Heap: In einem Max-Heap muss der am Wurzelknoten vorhandene Schlüssel der größte unter den Schlüsseln aller seiner untergeordneten Knoten sein. Die gleiche Eigenschaft muss rekursiv für alle Unterbäume in diesem Binärbaum gelten.
• Min-Heap: In einem Min-Heap muss der am Wurzelknoten vorhandene Schlüssel der minimale Schlüssel aller seiner untergeordneten Knoten sein. Die gleiche Eigenschaft muss rekursiv für alle Unterbäume in diesem Binärbaum gelten.

# importing 'heapq' to implement heap queue import heapq # initializing list li = [5, 7, 9, 1, 3] # using heapify to convert list into heap heapq.heapify(li) # printing created heap print ('The created heap is : ',end='') print (list(li)) # using heappush() to push elements into heap # pushes 4 heapq.heappush(li,4) # printing modified heap print ('The modified heap after push is : ',end='') print (list(li)) # using heappop() to pop smallest element print ('The popped and smallest element is : ',end='') print (heapq.heappop(li)) 

The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1 

Weitere Artikel zu Heap

• Binärer Heap
• K'tes größtes Element in einem Array
• K'tes kleinstes/größtes Element im unsortierten Array
• Sortieren Sie ein nahezu sortiertes Array
• K-tes zusammenhängendes Subarray mit der größten Summe
• Minimale Summe zweier Zahlen, die aus Ziffern eines Arrays gebildet werden

Ein Baum ist eine hierarchische Datenstruktur, die wie in der folgenden Abbildung aussieht –

 tree  ----  j  <-- root  /   f k  /   a h z  <-- leaves 

Der oberste Knoten des Baums wird als Wurzel bezeichnet, während die untersten Knoten oder Knoten ohne Kinder als Blattknoten bezeichnet werden. Die Knoten, die sich direkt unter einem Knoten befinden, werden als dessen untergeordnete Knoten bezeichnet, und die Knoten, die direkt über einem Knoten liegen, werden als dessen übergeordnete Knoten bezeichnet.

A Binärbaum ist ein Baum, dessen Elemente fast zwei Kinder haben können. Da jedes Element in einem Binärbaum nur zwei untergeordnete Elemente haben kann, nennen wir sie normalerweise das linke und das rechte untergeordnete Element. Ein Binärbaumknoten enthält die folgenden Teile.

• Daten
• Zeiger auf das linke untergeordnete Element
• Zeiger auf das richtige Kind

Beispiel: Knotenklasse definieren

# A Python class that represents an individual node # in a Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key 

Lassen Sie uns nun einen Baum mit 4 Knoten in Python erstellen. Nehmen wir an, die Baumstruktur sieht wie folgt aus:

 tree  ----  1  <-- root  /   2 3   /  4 

Beispiel: Daten zum Baum hinzufügen

# Python program to introduce Binary Tree # A class that represents an individual node in a # Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key # create root root = Node(1) ''' following is the tree after above statement  1  /   None None''' root.left = Node(2); root.right = Node(3); ''' 2 and 3 become left and right children of 1  1  /   2 3  /  /  None None None None''' root.left.left = Node(4); '''4 becomes left child of 2  1  /   2 3  /  /  4 None None None /  None None''' 

Baumdurchquerung

Bäume können überquert werden auf veschiedenen Wegen. Im Folgenden sind die allgemein verwendeten Methoden zum Überqueren von Bäumen aufgeführt. Betrachten wir den folgenden Baum –

 tree  ----  1  <-- root  /   2 3   /  4 5 

Tiefendurchquerungen:

• Reihenfolge (Links, Wurzel, Rechts): 4 2 5 1 3
• Vorbestellung (Root, Left, Right): 1 2 4 5 3
• Postorder (Links, Rechts, Root): 4 5 2 3 1

Algorithmus Inorder(Baum)

• Durchlaufen Sie den linken Teilbaum, d. h. rufen Sie Inorder(left-subtree) auf.
• Besuchen Sie die Wurzel.
• Durchqueren Sie den rechten Teilbaum, d. h. rufen Sie Inorder(right-subtree) auf.

Algorithmus-Vorbestellung (Baum)

• Besuchen Sie die Wurzel.
• Durchqueren Sie den linken Teilbaum, d. h. rufen Sie Preorder(left-subtree) auf.
• Durchqueren Sie den rechten Teilbaum, d. h. rufen Sie Preorder(right-subtree) auf.

Algorithmus Postanweisung(Baum)

• Durchqueren Sie den linken Teilbaum, d. h. rufen Sie Postorder(left-subtree) auf.
• Durchqueren Sie den rechten Teilbaum, d. h. rufen Sie Postorder(right-subtree) auf.
• Besuchen Sie die Wurzel.

# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do inorder tree traversal def printInorder(root): if root: # First recur on left child printInorder(root.left) # then print the data of node print(root.val), # now recur on right child printInorder(root.right) # A function to do postorder tree traversal def printPostorder(root): if root: # First recur on left child printPostorder(root.left) # the recur on right child printPostorder(root.right) # now print the data of node print(root.val), # A function to do preorder tree traversal def printPreorder(root): if root: # First print the data of node print(root.val), # Then recur on left child printPreorder(root.left) # Finally recur on right child printPreorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Preorder traversal of binary tree is') printPreorder(root) print('
Inorder traversal of binary tree is') printInorder(root) print('
Postorder traversal of binary tree is') printPostorder(root) 

Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1 

Zeitkomplexität – O(n)

Breitenorientierte oder ebene Ordnungsdurchquerung

Durchqueren der Level-Reihenfolge eines Baumes ist die Breitendurchquerung für den Baum. Die Ebenenreihenfolge des obigen Baums beträgt 1 2 3 4 5.

Für jeden Knoten wird zunächst der Knoten besucht und dann werden seine untergeordneten Knoten in eine FIFO-Warteschlange gestellt. Unten ist der Algorithmus dafür –

• Erstellen Sie eine leere Warteschlange q
• temp_node = root /*start from root*/
• Schleife, während temp_node nicht NULL ist
  • temp_node->data drucken.
  • Stellen Sie die Kinder von temp_node (zuerst die linken, dann die rechten Kinder) in die Warteschlange q
  • Entfernen Sie einen Knoten aus q

# Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self ,key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Vorderseite der Warteschlange drucken und # aus Warteschlange entfernen print (queue[0].data) node = queue.pop(0) # Linkes untergeordnetes Element in die Warteschlange stellen, wenn node.left nicht None ist: queue.append(node.left ) # Rechtes Kind in die Warteschlange stellen, wenn node.right nicht None ist: queue.append(node.right) # Treiberprogramm zum Testen der obigen Funktion root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print ('Level Order Traversal des Binärbaums ist -') printLevelOrder(root) 

Level Order Traversal of binary tree is - 1 2 3 4 5 

Zeitkomplexität: O(n)

Weitere Artikel zum Thema Binärbaum

• Einfügen in einen Binärbaum
• Löschen in einem Binärbaum
• Inorder Tree Traversal ohne Rekursion
• Inorder Tree Traversal ohne Rekursion und ohne Stack!
• Postorder-Durchquerung aus gegebenen Inorder- und Preorder-Durchquerungen drucken
• Finden Sie die Nachbestellungsdurchquerung von BST anhand der Vorbestellungsdurchquerung

Binärer Suchbaum ist eine knotenbasierte binäre Baumdatenstruktur mit den folgenden Eigenschaften:

# A utility function to search a given key in BST def search(root,key): # Base Cases: root is null or key is present at root if root is None or root.val == key: return root # Key is greater than root's key if root.val  < key: return search(root.right,key) # Key is smaller than root's key return search(root.left,key) 

# Python program to demonstrate # insert operation in binary search tree # A utility class that represents # an individual node in a BST class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A utility function to insert # a new node with the given key def insert(root, key): if root is None: return Node(key) else: if root.val == key: return root elif root.val  < key: root.right = insert(root.right, key) else: root.left = insert(root.left, key) return root # A utility function to do inorder tree traversal def inorder(root): if root: inorder(root.left) print(root.val) inorder(root.right) # Driver program to test the above functions # Let us create the following BST # 50 # /  # 30 70 # /  /  # 20 40 60 80 r = Node(50) r = insert(r, 30) r = insert(r, 20) r = insert(r, 40) r = insert(r, 70) r = insert(r, 60) r = insert(r, 80) # Print inorder traversal of the BST inorder(r) 

20 30 40 50 60 70 80 

A Graph ist eine nichtlineare Datenstruktur bestehend aus Knoten und Kanten. Die Knoten werden manchmal auch als Eckpunkte bezeichnet und die Kanten sind Linien oder Bögen, die zwei beliebige Knoten im Diagramm verbinden. Formaler kann ein Graph als ein Graph definiert werden, der aus einer endlichen Menge von Eckpunkten (oder Knoten) und einer Menge von Kanten besteht, die ein Knotenpaar verbinden.

# A simple representation of graph using Adjacency Matrix class Graph: def __init__(self,numvertex): self.adjMatrix = [[-1]*numvertex for x in range(numvertex)] self.numvertex = numvertex self.vertices = {} self.verticeslist =[0]*numvertex def set_vertex(self,vtx,id): if 0 <=vtx <=self.numvertex: self.vertices[id] = vtx self.verticeslist[vtx] = id def set_edge(self,frm,to,cost=0): frm = self.vertices[frm] to = self.vertices[to] self.adjMatrix[frm][to] = cost # for directed graph do not add this self.adjMatrix[to][frm] = cost def get_vertex(self): return self.verticeslist def get_edges(self): edges=[] for i in range (self.numvertex): for j in range (self.numvertex): if (self.adjMatrix[i][j]!=-1): edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j])) return edges def get_matrix(self): return self.adjMatrix G =Graph(6) G.set_vertex(0,'a') G.set_vertex(1,'b') G.set_vertex(2,'c') G.set_vertex(3,'d') G.set_vertex(4,'e') G.set_vertex(5,'f') G.set_edge('a','e',10) G.set_edge('a','c',20) G.set_edge('c','b',30) G.set_edge('b','e',40) G.set_edge('e','d',50) G.set_edge('f','e',60) print('Vertices of Graph') print(G.get_vertex()) print('Edges of Graph') print(G.get_edges()) print('Adjacency Matrix of Graph') print(G.get_matrix()) 

# A class to represent the adjacency list of the node class AdjNode: def __init__(self, data): self.vertex = data self.next = None # A class to represent a graph. A graph # is the list of the adjacency lists. # Size of the array will be the no. of the # vertices 'V' class Graph: def __init__(self, vertices): self.V = vertices self.graph = [None] * self.V # Function to add an edge in an undirected graph def add_edge(self, src, dest): # Adding the node to the source node node = AdjNode(dest) node.next = self.graph[src] self.graph[src] = node # Adding the source node to the destination as # it is the undirected graph node = AdjNode(src) node.next = self.graph[dest] self.graph[dest] = node # Function to print the graph def print_graph(self): for i in range(self.V): print('Adjacency list of vertex {}
 head'.format(i), end='') temp = self.graph[i] while temp: print(' ->{}'.format(temp.vertex), end='') temp = temp.next print(' 
') # Treiberprogramm für die obige Diagrammklasse, wenn __name__ == '__main__' : V = 5 graph = Graph(V) graph.add_edge(0, 1) graph.add_edge(0, 4) graph.add_edge(1, 2) graph.add_edge(1, 3) graph.add_edge(1, 4) graph.add_edge(2, 3) graph.add_edge(3, 4) graph.print_graph() 

Adjacency list of vertex 0 head ->4 -> 1 Adjazenzliste von Scheitelpunkt 1 Kopf -> 4 -> 3 -> 2 -> 0 Adjazenzliste von Scheitelpunkt 2 Kopf -> 3 -> 1 Adjazenzliste von Scheitelpunkt 3 Kopf -> 4 -> 2 -> 1 Adjazenz Liste von Scheitelpunkt 4 Kopf -> 3 -> 1 -> 0 

Breitenorientierte Durchquerung für einen Graphen ähnelt die Breitendurchquerung eines Baumes. Der einzige Haken hier ist, dass Diagramme im Gegensatz zu Bäumen Zyklen enthalten können, sodass wir möglicherweise wieder zum selben Knoten gelangen. Um zu vermeiden, dass ein Knoten mehr als einmal verarbeitet wird, verwenden wir ein boolesches besuchtes Array. Der Einfachheit halber wird angenommen, dass alle Scheitelpunkte vom Startscheitelpunkt aus erreichbar sind.

Im folgenden Diagramm beginnen wir beispielsweise mit der Durchquerung von Scheitelpunkt 2. Wenn wir Scheitelpunkt 0 erreichen, suchen wir nach allen angrenzenden Scheitelpunkten. 2 ist auch ein angrenzender Scheitelpunkt von 0. Wenn wir besuchte Scheitelpunkte nicht markieren, wird 2 erneut verarbeitet und es wird zu einem nicht terminierenden Prozess. Eine Breitendurchquerung des folgenden Diagramms ist 2, 0, 3, 1.

# Python3 Program to print BFS traversal # from a given source vertex. BFS(int s) # traverses vertices reachable from s. from collections import defaultdict # This class represents a directed graph # using adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self,u,v): self.graph[u].append(v) # Function to print a BFS of graph def BFS(self, s): # Mark all the vertices as not visited visited = [False] * (max(self.graph) + 1) # Create a queue for BFS queue = [] # Mark the source node as # visited and enqueue it queue.append(s) visited[s] = True while queue: # Dequeue a vertex from # queue and print it s = queue.pop(0) print (s, end = ' ') # Get all adjacent vertices of the # dequeued vertex s. If a adjacent # has not been visited, then mark it # visited and enqueue it for i in self.graph[s]: if visited[i] == False: queue.append(i) visited[i] = True # Driver code # Create a graph given in # the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print ('Following is Breadth First Traversal' ' (starting from vertex 2)') g.BFS(2) 

Following is Breadth First Traversal (starting from vertex 2) 2 0 3 1 

Zeitkomplexität: O(V+E), wobei V die Anzahl der Eckpunkte im Diagramm und E die Anzahl der Kanten im Diagramm ist.

Tiefensuche oder DFS

Tiefendurchquerung für ein Diagramm ähnelt der Tiefendurchquerung eines Baums. Der einzige Haken hier ist, dass Diagramme im Gegensatz zu Bäumen Zyklen enthalten können und ein Knoten möglicherweise zweimal besucht wird. Um zu vermeiden, dass ein Knoten mehr als einmal verarbeitet wird, verwenden Sie ein boolesches besuchtes Array.

Algorithmus:

• Erstellen Sie eine rekursive Funktion, die den Index des Knotens und ein besuchtes Array übernimmt.
• Markieren Sie den aktuellen Knoten als besucht und drucken Sie den Knoten aus.
• Durchlaufen Sie alle benachbarten und nicht markierten Knoten und rufen Sie die rekursive Funktion mit dem Index des benachbarten Knotens auf.

# Python3 program to print DFS traversal # from a given graph from collections import defaultdict # This class represents a directed graph using # adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self, u, v): self.graph[u].append(v) # A function used by DFS def DFSUtil(self, v, visited): # Mark the current node as visited # and print it visited.add(v) print(v, end=' ') # Recur for all the vertices # adjacent to this vertex for neighbour in self.graph[v]: if neighbour not in visited: self.DFSUtil(neighbour, visited) # The function to do DFS traversal. It uses # recursive DFSUtil() def DFS(self, v): # Create a set to store visited vertices visited = set() # Call the recursive helper function # to print DFS traversal self.DFSUtil(v, visited) # Driver code # Create a graph given # in the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print('Following is DFS from (starting from vertex 2)') g.DFS(2) 

Following is DFS from (starting from vertex 2) 2 0 1 3 

Weitere Artikel zum Thema Grafik

• Diagrammdarstellungen mit Set und Hash
• Finden Sie den Mutterscheitelpunkt in einem Diagramm
• Iterative Tiefensuche
• Zählen Sie mithilfe von BFS die Anzahl der Knoten auf einer bestimmten Ebene in einem Baum
• Zählen Sie alle möglichen Pfade zwischen zwei Eckpunkten

Der Vorgang, bei dem sich eine Funktion direkt oder indirekt selbst aufruft, heißt Rekursion und die entsprechende Funktion heißt a rekursive Funktion . Mit den rekursiven Algorithmen lassen sich bestimmte Probleme recht einfach lösen. Beispiele für solche Probleme sind Towers of Hanoi (TOH), Inorder/Preorder/Postorder Tree Traversals, DFS of Graph usw.

def fact(n):  # base case  if (n  <= 1)   return 1  else   return n*fact(n-1) 

# A Python 3 program to # demonstrate working of # recursion def printFun(test): if (test  < 1): return else: print(test, end=' ') printFun(test-1) # statement 2 print(test, end=' ') return # Driver Code test = 3 printFun(test) 

3 2 1 1 2 3 

• Rekursion
• Rekursion in Python
• Übungsfragen zur Rekursion | Set 1
• Übungsfragen zur Rekursion | Satz 2
• Übungsfragen zur Rekursion | Satz 3
• Übungsfragen zur Rekursion | Satz 4
• Übungsfragen zur Rekursion | Satz 5
• Übungsfragen zur Rekursion | Satz 6
• Übungsfragen zur Rekursion | Satz 7

>>> Mehr

Dynamische Programmierung

Dynamische Programmierung ist hauptsächlich eine Optimierung gegenüber der einfachen Rekursion. Wo immer wir eine rekursive Lösung sehen, die wiederholte Aufrufe für dieselben Eingaben enthält, können wir sie mithilfe der dynamischen Programmierung optimieren. Die Idee besteht darin, die Ergebnisse von Teilproblemen einfach zu speichern, damit wir sie bei Bedarf später nicht erneut berechnen müssen. Diese einfache Optimierung reduziert die Zeitkomplexität von exponentiell auf polynomial. Wenn wir beispielsweise eine einfache rekursive Lösung für Fibonacci-Zahlen schreiben, erhalten wir eine exponentielle Zeitkomplexität, und wenn wir sie optimieren, indem wir Lösungen von Teilproblemen speichern, reduziert sich die Zeitkomplexität auf linear.

Tabellierung vs. Auswendiglernen

Es gibt zwei unterschiedliche Möglichkeiten, die Werte zu speichern, sodass die Werte eines Teilproblems wiederverwendet werden können. Hier werden zwei Muster zur Lösung des Problems der dynamischen Programmierung (DP) diskutiert:

• Tabellierung: Von unten nach oben
• Auswendiglernen: Von oben nach unten

Tabellierung

Wie der Name schon sagt, beginnen Sie von unten und sammeln Sie Antworten nach oben. Lassen Sie uns im Hinblick auf den Zustandsübergang diskutieren.

Beschreiben wir einen Zustand für unser DP-Problem als dp[x] mit dp[0] als Basiszustand und dp[n] als unserem Zielzustand. Wir müssen also den Wert des Zielstatus ermitteln, d. h. dp[n].

Wenn wir unseren Übergang von unserem Basiszustand, d. h. dp[0], beginnen und unserer Zustandsübergangsrelation folgen, um unseren Zielzustand dp[n] zu erreichen, nennen wir das den Bottom-Up-Ansatz, da ganz klar ist, dass wir unseren Übergang von dort aus begonnen haben unteren Grundzustand und erreichte den obersten gewünschten Zustand.

Warum nennen wir es nun Tabellierungsmethode?

Um dies herauszufinden, schreiben wir zunächst Code, um die Fakultät einer Zahl mithilfe des Bottom-up-Ansatzes zu berechnen. Auch hier definieren wir als allgemeine Vorgehensweise zur Lösung eines DP zunächst einen Zustand. In diesem Fall definieren wir einen Zustand als dp[x], wobei dp[x] die Fakultät von x ermitteln soll.

Nun ist es ziemlich offensichtlich, dass dp[x+1] = dp[x] * (x+1)

# Tabulated version to find factorial x. dp = [0]*MAXN # base case dp[0] = 1; for i in range(n+1):  dp[i] = dp[i-1] * i 

Auswendiglernen

Lassen Sie es uns noch einmal anhand des Zustandsübergangs beschreiben. Wenn wir den Wert für einen Zustand finden müssen, sagen wir dp[n], und anstatt vom Basiszustand dp[0] auszugehen, erfragen wir unsere Antwort bei den Zuständen, die nach dem Zustandsübergang den Zielzustand dp[n] erreichen können Beziehung, dann ist es die Top-Down-Methode der DP.

Hier beginnen wir unsere Reise im obersten Zielstaat und berechnen die Antwort, indem wir die Werte der Staaten zählen, die den Zielstaat erreichen können, bis wir den untersten Basiszustand erreichen.

Lassen Sie uns den Code für das faktorielle Problem noch einmal von oben nach unten schreiben

# Memoized version to find factorial x. # To speed up we store the values # of calculated states # initialized to -1 dp[0]*MAXN # return fact x! def solve(x):  if (x==0)  return 1  if (dp[x]!=-1)  return dp[x]  return (dp[x] = x * solve(x-1)) 

Weitere Artikel zur dynamischen Programmierung

• Optimale Unterkonstruktionseigenschaft
• Eigenschaft „Überlappende Teilprobleme“.
• Fibonacci-Zahlen
• Teilmenge mit durch m teilbarer Summe
• Maximalsummenerhöhungsfolge
• Längster gemeinsamer Teilstring

>>> Mehr

Suchalgorithmen

Lineare Suche

• Beginnen Sie mit dem Element ganz links von arr[] und vergleichen Sie x nacheinander mit jedem Element von arr[]
• Wenn x mit einem Element übereinstimmt, wird der Index zurückgegeben.
• Wenn x mit keinem der Elemente übereinstimmt, wird -1 zurückgegeben.

# Python3 code to linearly search x in arr[]. # If x is present then return its location, # otherwise return -1 def search(arr, n, x): for i in range(0, n): if (arr[i] == x): return i return -1 # Driver Code arr = [2, 3, 4, 10, 40] x = 10 n = len(arr) # Function call result = search(arr, n, x) if(result == -1): print('Element is not present in array') else: print('Element is present at index', result) 

Element is present at index 3 

Die zeitliche Komplexität des obigen Algorithmus beträgt O(n).

Weitere Informationen finden Sie unter Lineare Suche .

Binäre Suche

Durchsuchen Sie ein sortiertes Array, indem Sie das Suchintervall wiederholt halbieren. Beginnen Sie mit einem Intervall, das das gesamte Array abdeckt. Wenn der Wert des Suchschlüssels kleiner ist als das Element in der Mitte des Intervalls, grenzen Sie das Intervall auf die untere Hälfte ein. Andernfalls beschränken Sie es auf die obere Hälfte. Überprüfen Sie wiederholt, bis der Wert gefunden wird oder das Intervall leer ist.

# Python3 Program for recursive binary search. # Returns index of x in arr if present, else -1 def binarySearch (arr, l, r, x): # Check base case if r>= l: mid = l + (r - l) // 2 # Wenn das Element in der Mitte selbst vorhanden ist, if arr[mid] == x: return mid # Wenn das Element kleiner als mid ist, kann es # nur vorhanden sein im linken Subarray elif arr[mid]> x: return BinarySearch(arr, l, mid-1, x) # Sonst kann das Element nur vorhanden sein # im rechten Subarray else: Return BinarySearch(arr, Mid + 1, r, x ) sonst: # Element ist im Array nicht vorhanden return -1 # Treibercode arr = [ 2, 3, 4, 10, 40 ] x = 10 # Funktionsaufrufergebnis = BinarySearch(arr, 0, len(arr)-1 , x) if result != -1: print ('Element ist am Index % d vorhanden' % result) else: print ('Element ist nicht im Array vorhanden') 

Element is present at index 3 

Die zeitliche Komplexität des obigen Algorithmus beträgt O(log(n)).

Weitere Informationen finden Sie unter Binäre Suche .

Sortieralgorithmen

Auswahlsortierung

Der Auswahl sortieren Der Algorithmus sortiert ein Array, indem er wiederholt das minimale Element (in aufsteigender Reihenfolge) aus dem unsortierten Teil findet und es an den Anfang setzt. Bei jeder Iteration der Auswahlsortierung wird das minimale Element (in aufsteigender Reihenfolge) aus dem unsortierten Subarray ausgewählt und in das sortierte Subarray verschoben.

Flussdiagramm der Auswahlsortierung:

# Python program for implementation of Selection # Sort import sys A = [64, 25, 12, 22, 11] # Traverse through all array elements for i in range(len(A)): # Find the minimum element in remaining # unsorted array min_idx = i for j in range(i+1, len(A)): if A[min_idx]>A[j]: min_idx = j # Tauschen Sie das gefundene minimale Element mit # dem ersten Element aus A[i], A[min_idx] = A[min_idx], A[i] # Treibercode zum Testen oben print ('Sorted array ') für i in range(len(A)): print('%d' %A[i]), 

Sorted array 11 12 22 25 64 

Zeitkomplexität: An ² ), da es zwei verschachtelte Schleifen gibt.

Hilfsraum: O(1)

Blasensortierung

Blasensortierung ist der einfachste Sortieralgorithmus, der durch wiederholtes Vertauschen benachbarter Elemente funktioniert, wenn sie in der falschen Reihenfolge sind.

Abbildung:

# Python program for implementation of Bubble Sort def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): # Last i elements are already in place for j in range(0, n-i-1): # traverse the array from 0 to n-i-1 # Swap if the element found is greater # than the next element if arr[j]>arr[j+1] : arr[j], arr[j+1] = arr[j+1], arr[j] # Treibercode zum Testen oben arr = [64, 34, 25, 12, 22, 11 , 90] bubbleSort(arr) print ('Sorted array is:') for i in range(len(arr)): print ('%d' %arr[i]), 

Sorted array is: 11 12 22 25 34 64 90 

Zeitkomplexität: An ² )

Sortieren durch Einfügen

So sortieren Sie ein Array der Größe n in aufsteigender Reihenfolge mit Sortieren durch Einfügen :

• Iterieren Sie von arr[1] zu arr[n] über das Array.
• Vergleichen Sie das aktuelle Element (Schlüssel) mit seinem Vorgänger.
• Wenn das Schlüsselelement kleiner als sein Vorgänger ist, vergleichen Sie es mit den vorherigen Elementen. Verschieben Sie die größeren Elemente um eine Position nach oben, um Platz für das ausgetauschte Element zu schaffen.

Illustration:

# Python program for implementation of Insertion Sort # Function to do insertion sort def insertionSort(arr): # Traverse through 1 to len(arr) for i in range(1, len(arr)): key = arr[i] # Move elements of arr[0..i-1], that are # greater than key, to one position ahead # of their current position j = i-1 while j>= 0 und Schlüssel < arr[j] : arr[j + 1] = arr[j] j -= 1 arr[j + 1] = key # Driver code to test above arr = [12, 11, 13, 5, 6] insertionSort(arr) for i in range(len(arr)): print ('% d' % arr[i]) 

 5 6 11 12 13 

Zeitkomplexität: An ² ))

Zusammenführen, sortieren

Wie QuickSort, Zusammenführen, sortieren ist ein Divide-and-Conquer-Algorithmus. Es teilt das Eingabearray in zwei Hälften, ruft sich selbst für die beiden Hälften auf und führt dann die beiden sortierten Hälften zusammen. Die Funktion merge() wird zum Zusammenführen zweier Hälften verwendet. Merge(arr, l, m, r) ist ein Schlüsselprozess, der davon ausgeht, dass arr[l..m] und arr[m+1..r] sortiert sind, und die beiden sortierten Unterarrays zu einem zusammenführt.

MergeSort(arr[], l, r) If r>l 1. Finden Sie den Mittelpunkt, um das Array in zwei Hälften zu teilen: middle m = l+ (r-l)/2 2. MergeSort für die erste Hälfte aufrufen: mergeSort(arr, l, m) aufrufen 3. mergeSort für die zweite Hälfte aufrufen: Call mergeSort(arr, m+1, r) 4. Führen Sie die beiden in Schritt 2 und 3 sortierten Hälften zusammen: Rufen Sie merge(arr, l, m, r)>'> auf   
     
Python3   
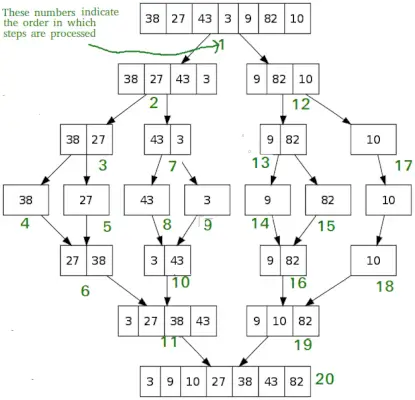
# Python program for implementation of MergeSort def mergeSort(arr): if len(arr)>1: # Finden der Mitte des Arrays mid = len(arr)//2 # Teilen der Array-Elemente L = arr[:mid] # in 2 Hälften R = arr[mid:] # Sortieren der ersten Hälfte mergeSort(L) # Sortieren der zweiten Hälfte mergeSort(R) i = j = k = 0 # Daten in die temporären Arrays L[] und R[] kopieren, während i < len(L) and j  < len(R): if L[i]  < R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 # Checking if any element was left while i  < len(L): arr[k] = L[i] i += 1 k += 1 while j  < len(R): arr[k] = R[j] j += 1 k += 1 # Code to print the list def printList(arr): for i in range(len(arr)): print(arr[i], end=' ') print() # Driver Code if __name__ == '__main__': arr = [12, 11, 13, 5, 6, 7] print('Given array is', end='
') printList(arr) mergeSort(arr) print('Sorted array is: ', end='
') printList(arr) 
    
  Ausgabe       Zeitkomplexität:     O(n(logn))  
  
 Schnelle Sorte  
 
 Wie Zusammenführungssortierung,    Schnelle Sorte    ist ein Divide-and-Conquer-Algorithmus. Es wählt ein Element als Pivot aus und partitioniert das angegebene Array um den ausgewählten Pivot. Es gibt viele verschiedene Versionen von QuickSort, die Pivot auf unterschiedliche Weise auswählen.  
  
 Wählen Sie immer das erste Element als Drehpunkt.  
  
 
 Wählen Sie immer das letzte Element als Pivot (unten implementiert)  
 
 Wählen Sie ein zufälliges Element als Pivot.  
 
 Wählen Sie den Median als Pivot.  
 
 
 Der Schlüsselprozess in QuickSort ist partition(). Das Ziel von Partitionen besteht darin, bei einem gegebenen Array und einem Element x des Arrays als Drehpunkt x an der richtigen Position im sortierten Array zu platzieren und alle kleineren Elemente (kleiner als x) vor x und alle größeren Elemente (größer als x) danach zu platzieren X. All dies sollte in linearer Zeit erfolgen.  
  
/* low -->Startindex, hoch --> Endindex */ quickSort(arr[], low, high) { if (low { /* pi ist Partitionierungsindex, arr[pi] ist jetzt an der richtigen Stelle */ pi = partition(arr, low, high); quickSort(arr, low, pi - 1); // Vor pi quickSort(arr, pi + 1, high); // Nach pi } 
 
  
  
    Partitionsalgorithmus     
  
 Es gibt viele Möglichkeiten, eine Partitionierung durchzuführen    Pseudocode    übernimmt die im CLRS-Buch angegebene Methode. Die Logik ist einfach: Wir beginnen mit dem Element ganz links und verfolgen den Index kleinerer (oder gleicher) Elemente wie i. Wenn wir beim Durchlaufen ein kleineres Element finden, tauschen wir das aktuelle Element mit arr[i] aus. Andernfalls ignorieren wir das aktuelle Element.  
  
/* This function takes last element as pivot, places the pivot element at its correct position in sorted array, and places all smaller (smaller than pivot) to left of pivot and all greater elements to right of pivot */ partition (arr[], low, high) {  // pivot (Element to be placed at right position)  pivot = arr[high];   i = (low – 1) // Index of smaller element and indicates the   // right position of pivot found so far  for (j = low; j  <= high- 1; j++){  // If current element is smaller than the pivot  if (arr[j]   i++; // increment index of smaller element  swap arr[i] and arr[j]  }  }  swap arr[i + 1] and arr[high])  return (i + 1) } 
Python3   
# Python3 implementation of QuickSort # This Function handles sorting part of quick sort # start and end points to first and last element of # an array respectively def partition(start, end, array): # Initializing pivot's index to start pivot_index = start pivot = array[pivot_index] # This loop runs till start pointer crosses # end pointer, and when it does we swap the # pivot with element on end pointer while start  < end: # Increment the start pointer till it finds an # element greater than pivot while start  < len(array) and array[start]  <= pivot: start += 1 # Decrement the end pointer till it finds an # element less than pivot while array[end]>Pivot: Ende -= 1 # Wenn sich Start und Ende nicht gekreuzt haben, # vertauschen Sie die Zahlen an Start und Ende if(start < end): array[start], array[end] = array[end], array[start] # Swap pivot element with element on end pointer. # This puts pivot on its correct sorted place. array[end], array[pivot_index] = array[pivot_index], array[end] # Returning end pointer to divide the array into 2 return end # The main function that implements QuickSort def quick_sort(start, end, array): if (start  < end): # p is partitioning index, array[p] # is at right place p = partition(start, end, array) # Sort elements before partition # and after partition quick_sort(start, p - 1, array) quick_sort(p + 1, end, array) # Driver code array = [ 10, 7, 8, 9, 1, 5 ] quick_sort(0, len(array) - 1, array) print(f'Sorted array: {array}') 
    
  Ausgabe   
Sorted array: [1, 5, 7, 8, 9, 10] 
  
    Zeitkomplexität:     O(n(logn))  
  
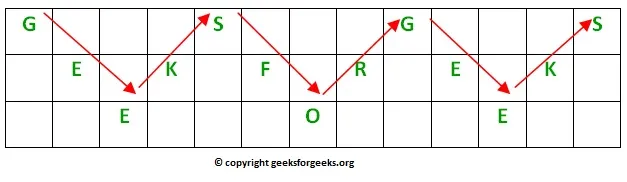
 ShellSort  
 
  ShellSort   ist hauptsächlich eine Variation von Insertion Sort. Bei der Einfügesortierung verschieben wir Elemente nur eine Position nach vorne. Wenn ein Element weit nach vorne bewegt werden muss, sind viele Bewegungen erforderlich. Die Idee von ShellSort besteht darin, den Austausch entfernter Elemente zu ermöglichen. In ShellSort machen wir das Array für einen großen Wert von h h-sortiert. Wir reduzieren den Wert von h so lange, bis er 1 wird. Ein Array wird als h-sortiert bezeichnet, wenn alle Unterlisten jedes hs vorhanden sind   Th   Element ist sortiert.  
Python3   
# Python3 program for implementation of Shell Sort def shellSort(arr): gap = len(arr) // 2 # initialize the gap while gap>0: i = 0 j = Lücke # Checke das Array von links nach rechts ein # bis zum letzten möglichen Index von j while j < len(arr): if arr[i]>arr[j]: arr[i],arr[j] = arr[j],arr[i] i += 1 j += 1 # Jetzt schauen wir vom i-ten Index nach links zurück # wir tauschen die Werte aus, die sind nicht in der richtigen Reihenfolge. k = i während k - Lücke> -1: wenn arr[k - Lücke]> arr[k]: arr[k-lücke],arr[k] = arr[k],arr[k-lücke] k -= 1 Lücke //= 2 # Treiber zum Überprüfen des Codes arr2 = [12, 34, 54, 2, 3] print('input array:',arr2) shellSort(arr2) print('sorted array', arr2) 
    
  Ausgabe   
input array: [12, 34, 54, 2, 3] sorted array [2, 3, 12, 34, 54] 
  
    Zeitkomplexität:     An   2   ).