Tangenter mellem to konvekse polygoner
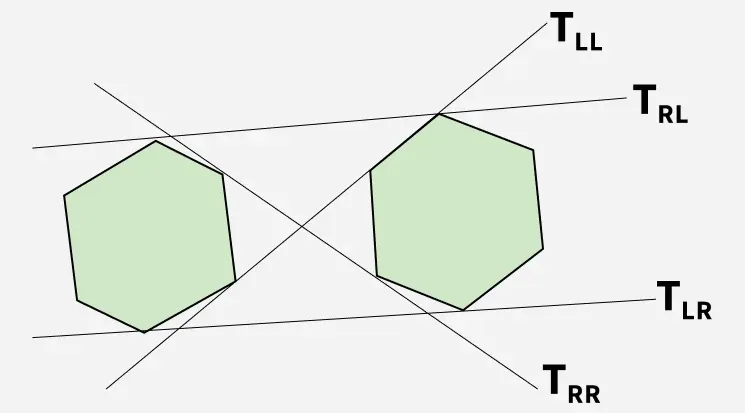
Med to konvekse polygoner sigter vi mod at identificere de nedre og øvre tangenter, der forbinder dem.
Som vist i figuren nedenfor T RL og T LR repræsenterer henholdsvis øvre og nedre tangenter.

Eksempler:
Input: Første polygon: [[2 2] [3 3] [5 2] [4 0] [3 1]]
Anden polygon: [[-1 0] [0 1] [1 0] [0 -2]].
Produktion: Øvre Tangent - linjeforbindelse (01) og (33)
Nedre Tangent - linjeforbindelse (0-2) og (40)
Forklaring: Billedet viser tydeligt strukturen og tangenterne, der forbinder de to polygoner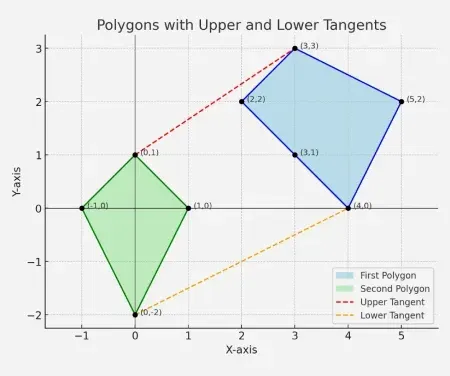
Nærme sig:
For at finde den øverste tangent begynder vi med at vælge to punkter: punktet længst til højre i polygonen -en og polygonens længst venstre punkt b . Linjen, der forbinder disse to punkter, er mærket som Linje 1 . Da denne linje går gennem polygon b (dvs. den er ikke helt over den) vi bevæger os til næste punkt i retning mod uret på b dannelse Linje 2 . Denne linje er nu over polygon b hvilket er godt. Men det krydser polygon -en så vi går videre til næste punkt -en i urets retning skaber Linje 3 . Linje 3 krydser stadig polygon -en beder om et andet træk til Linje 4 . Linje 4 krydser dog polygon b så vi går videre til Linje 5 . Endelig Linje 5 krydser ikke nogen polygon, hvilket gør den til den korrekte øvre tangent for de givne polygoner.
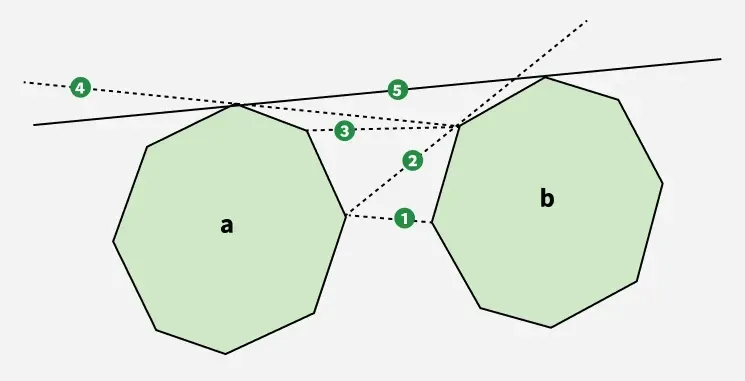
For at finde den nederste tangent skal vi bevæge os omvendt gennem polygonerne, dvs. hvis linjen krydser polygonen b, flytter vi til næste med uret og mod uret næste, hvis linjen krydser polygonen a.
Algoritme for øvre tangent:
L ← linje, der forbinder punktet længst til højre i a og punktet længst til venstre i b. while (L krydser enhver af polygonerne) { while(L krydser b) L ← L' : punktet på b rykker op. mens (L krydser a) L ← L': punktet på a rykker op. }
Algoritme for lavere tangent:
L ← linje, der forbinder punktet længst til højre i a og punktet længst til venstre i b. mens (L krydser enhver af polygonerne) { mens (L krydser b) L ← L' : punktet på b flyttes ned. mens (L krydser a) L ← L' : punktet på a flyttes ned. }
Bemærk, at ovenstående kode kun beregner den øvre tangent. En lignende tilgang kan også bruges til at finde den nederste tangent.
CPP #include using namespace std ; // Determines the quadrant of a point relative to origin int quad ( vector < int > p ) { if ( p [ 0 ] >= 0 && p [ 1 ] >= 0 ) return 1 ; if ( p [ 0 ] <= 0 && p [ 1 ] >= 0 ) return 2 ; if ( p [ 0 ] <= 0 && p [ 1 ] <= 0 ) return 3 ; return 4 ; } // Returns the orientation of ordered triplet (a b c) // 0 -> Collinear 1 -> Clockwise -1 -> Counterclockwise int orientation ( vector < int > a vector < int > b vector < int > c ) { int res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]); if ( res == 0 ) return 0 ; if ( res > 0 ) return 1 ; return -1 ; } // Compare function to sort points counter-clockwise around center bool compare ( vector < int > p1 vector < int > q1 vector < int > mid ) { vector < int > p = { p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ]}; vector < int > q = { q1 [ 0 ] - mid [ 0 ] q1 [ 1 ] - mid [ 1 ]}; int one = quad ( p ); int two = quad ( q ); if ( one != two ) return ( one < two ); return ( p [ 1 ] * q [ 0 ] < q [ 1 ] * p [ 0 ]); } // Sorts the polygon points counter-clockwise vector < vector < int >> sortPoints ( vector < vector < int >> polygon ) { vector < int > mid = { 0 0 }; int n = polygon . size (); // Calculate center (centroid) of the polygon for ( int i = 0 ; i < n ; i ++ ) { mid [ 0 ] += polygon [ i ][ 0 ]; mid [ 1 ] += polygon [ i ][ 1 ]; polygon [ i ][ 0 ] *= n ; polygon [ i ][ 1 ] *= n ; } // Sort points based on their angle from the center sort ( polygon . begin () polygon . end () [ mid ]( vector < int > p1 vector < int > p2 ) { return compare ( p1 p2 mid ); }); // Divide back to original coordinates for ( int i = 0 ; i < n ; i ++ ) { polygon [ i ][ 0 ] /= n ; polygon [ i ][ 1 ] /= n ; } return polygon ; } // Finds the upper tangent between two convex polygons a and b // Returns two points forming the upper tangent vector < vector < int >> findUpperTangent ( vector < vector < int >> a vector < vector < int >> b ) { int n1 = a . size () n2 = b . size (); // Find the rightmost point of polygon a and leftmost point of polygon b int maxa = INT_MIN ; for ( auto & p : a ) maxa = max ( maxa p [ 0 ]); int minb = INT_MAX ; for ( auto & p : b ) minb = min ( minb p [ 0 ]); // Sort both polygons counter-clockwise a = sortPoints ( a ); b = sortPoints ( b ); // Ensure polygon a is to the left of polygon b if ( minb < maxa ) swap ( a b ); n1 = a . size (); n2 = b . size (); // Find the rightmost point in a int ia = 0 ib = 0 ; for ( int i = 1 ; i < n1 ; i ++ ) if ( a [ i ][ 0 ] > a [ ia ][ 0 ]) ia = i ; // Find the leftmost point in b for ( int i = 1 ; i < n2 ; i ++ ) if ( b [ i ][ 0 ] < b [ ib ][ 0 ]) ib = i ; // Initialize starting points int inda = ia indb = ib ; bool done = false ; // Find upper tangent using orientation checks while ( ! done ) { done = true ; // Move to next point in a if necessary while ( orientation ( b [ indb ] a [ inda ] a [( inda + 1 ) % n1 ]) > 0 ) inda = ( inda + 1 ) % n1 ; // Move to previous point in b if necessary while ( orientation ( a [ inda ] b [ indb ] b [( n2 + indb - 1 ) % n2 ]) < 0 ) { indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } // Return the points forming the upper tangent return { a [ inda ] b [ indb ]}; } // Main driver code int main () { vector < vector < int >> a = {{ 2 2 } { 3 1 } { 3 3 } { 5 2 } { 4 0 }}; vector < vector < int >> b = {{ 0 1 } { 1 0 } { 0 -2 } { -1 0 }}; vector < vector < int >> tangent = findUpperTangent ( a b ); for ( auto it : tangent ){ cout < < it [ 0 ] < < ' ' < < it [ 1 ] < < ' n ' ; } return 0 ; }
Java import java.util.* ; class GfG { // Determines the quadrant of a point static int quad ( int [] p ) { if ( p [ 0 ] >= 0 && p [ 1 ] >= 0 ) return 1 ; if ( p [ 0 ] <= 0 && p [ 1 ] >= 0 ) return 2 ; if ( p [ 0 ] <= 0 && p [ 1 ] <= 0 ) return 3 ; return 4 ; } // Checks whether the line is crossing the polygon static int orientation ( int [] a int [] b int [] c ) { int res = ( b [ 1 ] - a [ 1 ] ) * ( c [ 0 ] - b [ 0 ] ) - ( c [ 1 ] - b [ 1 ] ) * ( b [ 0 ] - a [ 0 ] ); if ( res == 0 ) return 0 ; if ( res > 0 ) return 1 ; return - 1 ; } // Compare function for sorting static class PointComparator implements Comparator < int []> { int [] mid ; public PointComparator ( int [] mid ) { this . mid = mid ; } public int compare ( int [] p1 int [] p2 ) { int [] p = { p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ] }; int [] q = { p2 [ 0 ] - mid [ 0 ] p2 [ 1 ] - mid [ 1 ] }; int one = quad ( p ); int two = quad ( q ); if ( one != two ) return one - two ; return p [ 1 ] * q [ 0 ] - q [ 1 ] * p [ 0 ] ; } } // Finds upper tangent of two polygons 'a' and 'b' // represented as 2D arrays and stores the result static int [][] findUpperTangent ( int [][] a int [][] b ) { // n1 -> number of points in polygon a // n2 -> number of points in polygon b int n1 = a . length n2 = b . length ; int [] mid = { 0 0 }; int maxa = Integer . MIN_VALUE ; // Calculate centroid for polygon a and adjust points for scaling for ( int i = 0 ; i < n1 ; i ++ ) { maxa = Math . max ( maxa a [ i ][ 0 ] ); mid [ 0 ] += a [ i ][ 0 ] ; mid [ 1 ] += a [ i ][ 1 ] ; a [ i ][ 0 ] *= n1 ; a [ i ][ 1 ] *= n1 ; } // Sorting the points in counter-clockwise order for polygon a Arrays . sort ( a new PointComparator ( mid )); for ( int i = 0 ; i < n1 ; i ++ ) { a [ i ][ 0 ] /= n1 ; a [ i ][ 1 ] /= n1 ; } mid [ 0 ] = 0 ; mid [ 1 ] = 0 ; int minb = Integer . MAX_VALUE ; // Calculate centroid for polygon b and adjust points for scaling for ( int i = 0 ; i < n2 ; i ++ ) { mid [ 0 ] += b [ i ][ 0 ] ; mid [ 1 ] += b [ i ][ 1 ] ; minb = Math . min ( minb b [ i ][ 0 ] ); b [ i ][ 0 ] *= n2 ; b [ i ][ 1 ] *= n2 ; } // Sorting the points in counter-clockwise order for polygon b Arrays . sort ( b new PointComparator ( mid )); for ( int i = 0 ; i < n2 ; i ++ ) { b [ i ][ 0 ] /= n2 ; b [ i ][ 1 ] /= n2 ; } // If a is to the right of b swap a and b if ( minb < maxa ) { int [][] temp = a ; a = b ; b = temp ; n1 = a . length ; n2 = b . length ; } // ia -> rightmost point of a int ia = 0 ib = 0 ; for ( int i = 1 ; i < n1 ; i ++ ) { if ( a [ i ][ 0 ] > a [ ia ][ 0 ] ) ia = i ; } // ib -> leftmost point of b for ( int i = 1 ; i < n2 ; i ++ ) { if ( b [ i ][ 0 ] < b [ ib ][ 0 ] ) ib = i ; } // Finding the upper tangent int inda = ia indb = ib ; boolean done = false ; while ( ! done ) { done = true ; while ( orientation ( b [ indb ] a [ inda ] a [ ( inda + 1 ) % n1 ] ) > 0 ) inda = ( inda + 1 ) % n1 ; while ( orientation ( a [ inda ] b [ indb ] b [ ( n2 + indb - 1 ) % n2 ] ) < 0 ) { indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } // Returning the upper tangent as a 2D array return new int [][] { { a [ inda ][ 0 ] a [ inda ][ 1 ] } { b [ indb ][ 0 ] b [ indb ][ 1 ] } }; } // Driver code public static void main ( String [] args ) { int [][] a = {{ 2 2 }{ 3 1 }{ 3 3 }{ 5 2 }{ 4 0 }}; int [][] b = {{ 0 1 }{ 1 0 }{ 0 - 2 }{ - 1 0 }}; // Get the upper tangent as a 2D array int [][] upperTangent = findUpperTangent ( a b ); // Store or use the result System . out . println ( upperTangent [ 0 ][ 0 ] + ' ' + upperTangent [ 0 ][ 1 ] ); System . out . println ( upperTangent [ 1 ][ 0 ] + ' ' + upperTangent [ 1 ][ 1 ] ); } }
Python from functools import cmp_to_key def quad ( p ): if p [ 0 ] >= 0 and p [ 1 ] >= 0 : return 1 if p [ 0 ] <= 0 and p [ 1 ] >= 0 : return 2 if p [ 0 ] <= 0 and p [ 1 ] <= 0 : return 3 return 4 def orientation ( a b c ): res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]) if res == 0 : return 0 if res > 0 : return 1 return - 1 def compare ( mid ): def cmp ( p1 q1 ): p = [ p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ]] q = [ q1 [ 0 ] - mid [ 0 ] q1 [ 1 ] - mid [ 1 ]] one = quad ( p ) two = quad ( q ) if one != two : return one - two if p [ 1 ] * q [ 0 ] < q [ 1 ] * p [ 0 ]: return - 1 return 1 return cmp def findUpperTangent ( a b ): n1 n2 = len ( a ) len ( b ) mid_a = [ 0 0 ] maxa = float ( '-inf' ) for i in range ( n1 ): maxa = max ( maxa a [ i ][ 0 ]) mid_a [ 0 ] += a [ i ][ 0 ] mid_a [ 1 ] += a [ i ][ 1 ] a = sorted ( a key = cmp_to_key ( compare ( mid_a ))) mid_b = [ 0 0 ] minb = float ( 'inf' ) for i in range ( n2 ): minb = min ( minb b [ i ][ 0 ]) mid_b [ 0 ] += b [ i ][ 0 ] mid_b [ 1 ] += b [ i ][ 1 ] b = sorted ( b key = cmp_to_key ( compare ( mid_b ))) if minb < maxa : a b = b a n1 n2 = n2 n1 ia = 0 for i in range ( 1 n1 ): if a [ i ][ 0 ] > a [ ia ][ 0 ]: ia = i ib = 0 for i in range ( 1 n2 ): if b [ i ][ 0 ] < b [ ib ][ 0 ]: ib = i inda indb = ia ib done = False while not done : done = True while orientation ( b [ indb ] a [ inda ] a [( inda + 1 ) % n1 ]) > 0 : inda = ( inda + 1 ) % n1 while orientation ( a [ inda ] b [ indb ] b [( n2 + indb - 1 ) % n2 ]) < 0 : indb = ( n2 + indb - 1 ) % n2 done = False # return integer coordinates return [[ int ( a [ inda ][ 0 ]) int ( a [ inda ][ 1 ])] [ int ( b [ indb ][ 0 ]) int ( b [ indb ][ 1 ])]] # Driver Code if __name__ == '__main__' : a = [ [ 2 2 ] [ 3 1 ] [ 3 3 ] [ 5 2 ] [ 4 0 ] ] b = [ [ 0 1 ] [ 1 0 ] [ 0 - 2 ] [ - 1 0 ] ] upperTangent = findUpperTangent ( a b ) for point in upperTangent : print ( f ' { point [ 0 ] } { point [ 1 ] } ' )
C# using System ; public class UpperTangentFinder { static int Quad ( int x int y ) { if ( x >= 0 && y >= 0 ) return 1 ; if ( x <= 0 && y >= 0 ) return 2 ; if ( x <= 0 && y <= 0 ) return 3 ; return 4 ; } static int Orientation ( int [] a int [] b int [] c ) { int res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]); if ( res == 0 ) return 0 ; return res > 0 ? 1 : - 1 ; } static bool Compare ( int [] p1 int [] p2 int [] mid ) { int [] p = { p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ] }; int [] q = { p2 [ 0 ] - mid [ 0 ] p2 [ 1 ] - mid [ 1 ] }; int quadP = Quad ( p [ 0 ] p [ 1 ]); int quadQ = Quad ( q [ 0 ] q [ 1 ]); if ( quadP != quadQ ) return quadP < quadQ ; return ( p [ 1 ] * q [ 0 ]) < ( q [ 1 ] * p [ 0 ]); } static int [] SortPoints ( int [] polygon ) { int n = polygon . GetLength ( 0 ); int [] mid = { 0 0 }; for ( int i = 0 ; i < n ; i ++ ) { mid [ 0 ] += polygon [ i 0 ]; mid [ 1 ] += polygon [ i 1 ]; polygon [ i 0 ] *= n ; polygon [ i 1 ] *= n ; } for ( int i = 0 ; i < n - 1 ; i ++ ) { for ( int j = i + 1 ; j < n ; j ++ ) { int [] p1 = { polygon [ i 0 ] polygon [ i 1 ] }; int [] p2 = { polygon [ j 0 ] polygon [ j 1 ] }; if ( ! Compare ( p1 p2 mid )) { int tempX = polygon [ i 0 ] tempY = polygon [ i 1 ]; polygon [ i 0 ] = polygon [ j 0 ]; polygon [ i 1 ] = polygon [ j 1 ]; polygon [ j 0 ] = tempX ; polygon [ j 1 ] = tempY ; } } } for ( int i = 0 ; i < n ; i ++ ) { polygon [ i 0 ] /= n ; polygon [ i 1 ] /= n ; } return polygon ; } static int [] FindUpperTangent ( int [] a int [] b ) { int n1 = a . GetLength ( 0 ); int n2 = b . GetLength ( 0 ); int maxa = int . MinValue ; for ( int i = 0 ; i < n1 ; i ++ ) maxa = Math . Max ( maxa a [ i 0 ]); int minb = int . MaxValue ; for ( int i = 0 ; i < n2 ; i ++ ) minb = Math . Min ( minb b [ i 0 ]); a = SortPoints ( a ); b = SortPoints ( b ); if ( minb < maxa ) { int [] temp = a ; a = b ; b = temp ; n1 = a . GetLength ( 0 ); n2 = b . GetLength ( 0 ); } int ia = 0 ib = 0 ; for ( int i = 1 ; i < n1 ; i ++ ) if ( a [ i 0 ] > a [ ia 0 ]) ia = i ; for ( int i = 1 ; i < n2 ; i ++ ) if ( b [ i 0 ] < b [ ib 0 ]) ib = i ; int inda = ia indb = ib ; bool done = false ; while ( ! done ) { done = true ; while ( Orientation ( new int [] { b [ indb 0 ] b [ indb 1 ] } new int [] { a [ inda 0 ] a [ inda 1 ] } new int [] { a [( inda + 1 ) % n1 0 ] a [( inda + 1 ) % n1 1 ] }) > 0 ){ inda = ( inda + 1 ) % n1 ; } while ( Orientation ( new int [] { a [ inda 0 ] a [ inda 1 ] } new int [] { b [ indb 0 ] b [ indb 1 ] } new int [] { b [( n2 + indb - 1 ) % n2 0 ] b [( n2 + indb - 1 ) % n2 1 ] }) < 0 ){ indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } int [] result = new int [ 2 2 ]; result [ 0 0 ] = a [ inda 0 ]; result [ 0 1 ] = a [ inda 1 ]; result [ 1 0 ] = b [ indb 0 ]; result [ 1 1 ] = b [ indb 1 ]; return result ; } public static void Main ( string [] args ) { int [] a = new int [] { { 2 2 } { 3 1 } { 3 3 } { 5 2 } { 4 0 } }; int [] b = new int [] { { 0 1 } { 1 0 } { 0 - 2 } { - 1 0 } }; int [] tangent = FindUpperTangent ( a b ); for ( int i = 0 ; i < 2 ; i ++ ) { Console . WriteLine ( tangent [ i 0 ] + ' ' + tangent [ i 1 ]); } } }
JavaScript // Determine the quadrant of a point function quad ( p ) { if ( p [ 0 ] >= 0 && p [ 1 ] >= 0 ) return 1 ; if ( p [ 0 ] <= 0 && p [ 1 ] >= 0 ) return 2 ; if ( p [ 0 ] <= 0 && p [ 1 ] <= 0 ) return 3 ; return 4 ; } // Find orientation of triplet (a b c) function orientation ( a b c ) { let res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]); if ( res === 0 ) return 0 ; return res > 0 ? 1 : - 1 ; } // Compare two points based on mid function compare ( p1 p2 mid ) { let p = [ p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ]]; let q = [ p2 [ 0 ] - mid [ 0 ] p2 [ 1 ] - mid [ 1 ]]; let quadP = quad ( p ); let quadQ = quad ( q ); if ( quadP !== quadQ ) return quadP - quadQ ; return ( p [ 1 ] * q [ 0 ]) - ( q [ 1 ] * p [ 0 ]); } // Sort polygon points counter-clockwise function sortPoints ( polygon ) { let n = polygon . length ; let mid = [ 0 0 ]; for ( let i = 0 ; i < n ; i ++ ) { mid [ 0 ] += polygon [ i ][ 0 ]; mid [ 1 ] += polygon [ i ][ 1 ]; polygon [ i ][ 0 ] *= n ; polygon [ i ][ 1 ] *= n ; } polygon . sort (( p1 p2 ) => compare ( p1 p2 mid )); for ( let i = 0 ; i < n ; i ++ ) { polygon [ i ][ 0 ] = Math . floor ( polygon [ i ][ 0 ] / n ); polygon [ i ][ 1 ] = Math . floor ( polygon [ i ][ 1 ] / n ); } return polygon ; } // Find upper tangent between two convex polygons function findUpperTangent ( a b ) { let n1 = a . length ; let n2 = b . length ; let maxa = - Infinity ; for ( let i = 0 ; i < n1 ; i ++ ) maxa = Math . max ( maxa a [ i ][ 0 ]); let minb = Infinity ; for ( let i = 0 ; i < n2 ; i ++ ) minb = Math . min ( minb b [ i ][ 0 ]); a = sortPoints ( a ); b = sortPoints ( b ); if ( minb < maxa ) { let temp = a ; a = b ; b = temp ; n1 = a . length ; n2 = b . length ; } let ia = 0 ib = 0 ; for ( let i = 1 ; i < n1 ; i ++ ) if ( a [ i ][ 0 ] > a [ ia ][ 0 ]) ia = i ; for ( let i = 1 ; i < n2 ; i ++ ) if ( b [ i ][ 0 ] < b [ ib ][ 0 ]) ib = i ; let inda = ia indb = ib ; let done = false ; while ( ! done ) { done = true ; while ( orientation ( b [ indb ] a [ inda ] a [( inda + 1 ) % n1 ]) > 0 ) inda = ( inda + 1 ) % n1 ; while ( orientation ( a [ inda ] b [ indb ] b [( n2 + indb - 1 ) % n2 ]) < 0 ) { indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } return [ a [ inda ] b [ indb ]]; } // Driver code let a = [[ 2 2 ][ 3 1 ][ 3 3 ][ 5 2 ][ 4 0 ]]; let b = [[ 0 1 ][ 1 0 ][ 0 - 2 ][ - 1 0 ]]; let tangent = findUpperTangent ( a b ); for ( let point of tangent ) { console . log ( point [ 0 ] + ' ' + point [ 1 ]); }
Produktion
upper tangent (01) (33)
Tidskompleksitet: O(n1 log (n1) + n2 log(n2))
Hjælpeplads: O(1)