Omvendt sletningsalgoritme for minimumsspændingstræ

 #practiceLinkDiv { display: ingen !important; }
#practiceLinkDiv { display: ingen !important; } Omvendt sletningsalgoritme er tæt forbundet med Kruskals algoritme . I Kruskals algoritme er det, vi gør: Sortere kanter efter stigende rækkefølge af deres vægte. Efter sortering plukker vi en efter en kanter i stigende rækkefølge. Vi inkluderer aktuelt plukket kant, hvis ved at inkludere dette i spændingstræ ikke danner nogen cyklus, før der er V-1 kanter i spændingstræet, hvor V = antal hjørner.
I Reverse Delete-algoritmen sorterer vi alle kanter ind faldende rækkefølgen af deres vægte. Efter sortering plukker vi en efter en kanter i faldende rækkefølge. Vi inkludere den valgte flanke, hvis udelukkelse af den aktuelle flanke forårsager afbrydelse i den aktuelle graf . Hovedideen er slet kant, hvis sletningen ikke fører til afbrydelse af grafen.
Algoritmen:
- Sorter alle kanter af grafen i ikke-stigende rækkefølge af kantvægte.
- Initialiser MST som original graf og fjern ekstra kanter ved hjælp af trin 3.
- Vælg den højeste vægt kant fra de resterende kanter og kontrollere, om sletning af kanten afbryder grafen eller ej .
Hvis forbindelsen afbrydes, sletter vi ikke kanten.
Ellers sletter vi kanten og fortsætter.
Illustration:
Lad os forstå med følgende eksempel:
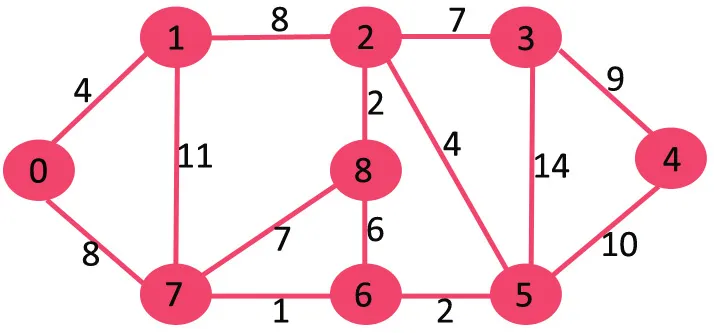
Hvis vi sletter den højeste vægtkant af vægt 14, bliver grafen ikke afbrudt, så vi fjerner den.
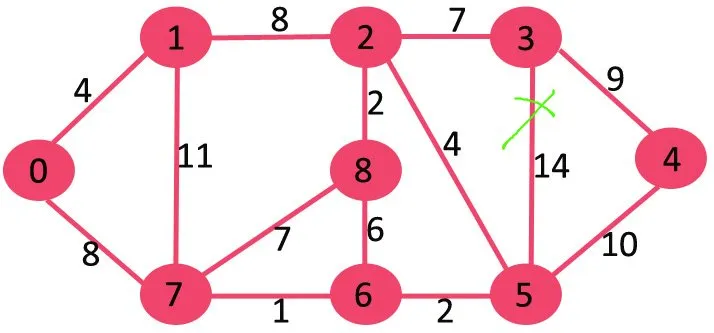
Dernæst sletter vi 11, da sletning ikke afbryder grafen.
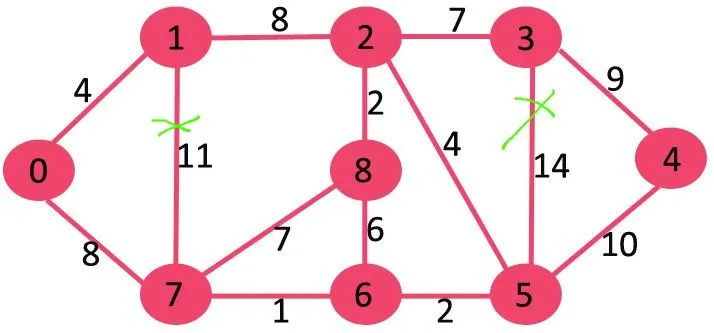
Dernæst sletter vi 10, da sletning ikke afbryder grafen.

Næste er 9. Vi kan ikke slette 9, da sletning af den forårsager afbrydelse af forbindelsen.

Vi fortsætter på denne måde, og følgende kanter forbliver i den endelige MST.
Edges in MST
(3 4)
(0 7)
(2 3)
(2 5)
(0 1)
(5 6)
(2 8)
(6 7)
Bemærk: I tilfælde af samme vægtkanter kan vi vælge enhver kant af samme vægtkanter.
Anbefalet praksis Omvendt sletningsalgoritme for minimumsspændingstræ Prøv det!Implementering:
C++Java// C++ program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm #includeusing namespace std ; // Creating shortcut for an integer pair typedef pair < int int > iPair ; // Graph class represents a directed graph // using adjacency list representation class Graph { int V ; // No. of vertices list < int > * adj ; vector < pair < int iPair > > edges ; void DFS ( int v bool visited []); public : Graph ( int V ); // Constructor // function to add an edge to graph void addEdge ( int u int v int w ); // Returns true if graph is connected bool isConnected (); void reverseDeleteMST (); }; Graph :: Graph ( int V ) { this -> V = V ; adj = new list < int > [ V ]; } void Graph :: addEdge ( int u int v int w ) { adj [ u ]. push_back ( v ); // Add w to v’s list. adj [ v ]. push_back ( u ); // Add w to v’s list. edges . push_back ({ w { u v }}); } void Graph :: DFS ( int v bool visited []) { // Mark the current node as visited and print it visited [ v ] = true ; // Recur for all the vertices adjacent to // this vertex list < int >:: iterator i ; for ( i = adj [ v ]. begin (); i != adj [ v ]. end (); ++ i ) if ( ! visited [ * i ]) DFS ( * i visited ); } // Returns true if given graph is connected else false bool Graph :: isConnected () { bool visited [ V ]; memset ( visited false sizeof ( visited )); // Find all reachable vertices from first vertex DFS ( 0 visited ); // If set of reachable vertices includes all // return true. for ( int i = 1 ; i < V ; i ++ ) if ( visited [ i ] == false ) return false ; return true ; } // This function assumes that edge (u v) // exists in graph or not void Graph :: reverseDeleteMST () { // Sort edges in increasing order on basis of cost sort ( edges . begin () edges . end ()); int mst_wt = 0 ; // Initialize weight of MST cout < < 'Edges in MST n ' ; // Iterate through all sorted edges in // decreasing order of weights for ( int i = edges . size () -1 ; i >= 0 ; i -- ) { int u = edges [ i ]. second . first ; int v = edges [ i ]. second . second ; // Remove edge from undirected graph adj [ u ]. remove ( v ); adj [ v ]. remove ( u ); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if ( isConnected () == false ) { adj [ u ]. push_back ( v ); adj [ v ]. push_back ( u ); // This edge is part of MST cout < < '(' < < u < < ' ' < < v < < ') n ' ; mst_wt += edges [ i ]. first ; } } cout < < 'Total weight of MST is ' < < mst_wt ; } // Driver code int main () { // create the graph given in above figure int V = 9 ; Graph g ( V ); // making above shown graph g . addEdge ( 0 1 4 ); g . addEdge ( 0 7 8 ); g . addEdge ( 1 2 8 ); g . addEdge ( 1 7 11 ); g . addEdge ( 2 3 7 ); g . addEdge ( 2 8 2 ); g . addEdge ( 2 5 4 ); g . addEdge ( 3 4 9 ); g . addEdge ( 3 5 14 ); g . addEdge ( 4 5 10 ); g . addEdge ( 5 6 2 ); g . addEdge ( 6 7 1 ); g . addEdge ( 6 8 6 ); g . addEdge ( 7 8 7 ); g . reverseDeleteMST (); return 0 ; } Python3// Java program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm import java.util.* ; // class to represent an edge class Edge implements Comparable < Edge > { int u v w ; Edge ( int u int v int w ) { this . u = u ; this . w = w ; this . v = v ; } public int compareTo ( Edge other ) { return ( this . w - other . w ); } } // Class to represent a graph using adjacency list // representation public class GFG { private int V ; // No. of vertices private List < Integer >[] adj ; private List < Edge > edges ; @SuppressWarnings ({ 'unchecked' 'deprecated' }) public GFG ( int v ) // Constructor { V = v ; adj = new ArrayList [ v ] ; for ( int i = 0 ; i < v ; i ++ ) adj [ i ] = new ArrayList < Integer > (); edges = new ArrayList < Edge > (); } // function to Add an edge public void AddEdge ( int u int v int w ) { adj [ u ] . add ( v ); // Add w to v’s list. adj [ v ] . add ( u ); // Add w to v’s list. edges . add ( new Edge ( u v w )); } // function to perform dfs private void DFS ( int v boolean [] visited ) { // Mark the current node as visited and print it visited [ v ] = true ; // Recur for all the vertices adjacent to // this vertex for ( int i : adj [ v ] ) { if ( ! visited [ i ] ) DFS ( i visited ); } } // Returns true if given graph is connected else false private boolean IsConnected () { boolean [] visited = new boolean [ V ] ; // Find all reachable vertices from first vertex DFS ( 0 visited ); // If set of reachable vertices includes all // return true. for ( int i = 1 ; i < V ; i ++ ) { if ( visited [ i ] == false ) return false ; } return true ; } // This function assumes that edge (u v) // exists in graph or not public void ReverseDeleteMST () { // Sort edges in increasing order on basis of cost Collections . sort ( edges ); int mst_wt = 0 ; // Initialize weight of MST System . out . println ( 'Edges in MST' ); // Iterate through all sorted edges in // decreasing order of weights for ( int i = edges . size () - 1 ; i >= 0 ; i -- ) { int u = edges . get ( i ). u ; int v = edges . get ( i ). v ; // Remove edge from undirected graph adj [ u ] . remove ( adj [ u ] . indexOf ( v )); adj [ v ] . remove ( adj [ v ] . indexOf ( u )); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if ( IsConnected () == false ) { adj [ u ] . add ( v ); adj [ v ] . add ( u ); // This edge is part of MST System . out . println ( '(' + u + ' ' + v + ')' ); mst_wt += edges . get ( i ). w ; } } System . out . println ( 'Total weight of MST is ' + mst_wt ); } // Driver code public static void main ( String [] args ) { // create the graph given in above figure int V = 9 ; GFG g = new GFG ( V ); // making above shown graph g . AddEdge ( 0 1 4 ); g . AddEdge ( 0 7 8 ); g . AddEdge ( 1 2 8 ); g . AddEdge ( 1 7 11 ); g . AddEdge ( 2 3 7 ); g . AddEdge ( 2 8 2 ); g . AddEdge ( 2 5 4 ); g . AddEdge ( 3 4 9 ); g . AddEdge ( 3 5 14 ); g . AddEdge ( 4 5 10 ); g . AddEdge ( 5 6 2 ); g . AddEdge ( 6 7 1 ); g . AddEdge ( 6 8 6 ); g . AddEdge ( 7 8 7 ); g . ReverseDeleteMST (); } } // This code is contributed by Prithi_DeyC## Python3 program to find Minimum Spanning Tree # of a graph using Reverse Delete Algorithm # Graph class represents a directed graph # using adjacency list representation class Graph : def __init__ ( self v ): # No. of vertices self . v = v self . adj = [ 0 ] * v self . edges = [] for i in range ( v ): self . adj [ i ] = [] # function to add an edge to graph def addEdge ( self u : int v : int w : int ): self . adj [ u ] . append ( v ) # Add w to v’s list. self . adj [ v ] . append ( u ) # Add w to v’s list. self . edges . append (( w ( u v ))) def dfs ( self v : int visited : list ): # Mark the current node as visited and print it visited [ v ] = True # Recur for all the vertices adjacent to # this vertex for i in self . adj [ v ]: if not visited [ i ]: self . dfs ( i visited ) # Returns true if graph is connected # Returns true if given graph is connected else false def connected ( self ): visited = [ False ] * self . v # Find all reachable vertices from first vertex self . dfs ( 0 visited ) # If set of reachable vertices includes all # return true. for i in range ( 1 self . v ): if not visited [ i ]: return False return True # This function assumes that edge (u v) # exists in graph or not def reverseDeleteMST ( self ): # Sort edges in increasing order on basis of cost self . edges . sort ( key = lambda a : a [ 0 ]) mst_wt = 0 # Initialize weight of MST print ( 'Edges in MST' ) # Iterate through all sorted edges in # decreasing order of weights for i in range ( len ( self . edges ) - 1 - 1 - 1 ): u = self . edges [ i ][ 1 ][ 0 ] v = self . edges [ i ][ 1 ][ 1 ] # Remove edge from undirected graph self . adj [ u ] . remove ( v ) self . adj [ v ] . remove ( u ) # Adding the edge back if removing it # causes disconnection. In this case this # edge becomes part of MST. if self . connected () == False : self . adj [ u ] . append ( v ) self . adj [ v ] . append ( u ) # This edge is part of MST print ( '( %d %d )' % ( u v )) mst_wt += self . edges [ i ][ 0 ] print ( 'Total weight of MST is' mst_wt ) # Driver Code if __name__ == '__main__' : # create the graph given in above figure V = 9 g = Graph ( V ) # making above shown graph g . addEdge ( 0 1 4 ) g . addEdge ( 0 7 8 ) g . addEdge ( 1 2 8 ) g . addEdge ( 1 7 11 ) g . addEdge ( 2 3 7 ) g . addEdge ( 2 8 2 ) g . addEdge ( 2 5 4 ) g . addEdge ( 3 4 9 ) g . addEdge ( 3 5 14 ) g . addEdge ( 4 5 10 ) g . addEdge ( 5 6 2 ) g . addEdge ( 6 7 1 ) g . addEdge ( 6 8 6 ) g . addEdge ( 7 8 7 ) g . reverseDeleteMST () # This code is contributed by # sanjeev2552JavaScript// C# program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm using System ; using System.Collections.Generic ; // class to represent an edge public class Edge : IComparable < Edge > { public int u v w ; public Edge ( int u int v int w ) { this . u = u ; this . v = v ; this . w = w ; } public int CompareTo ( Edge other ) { return this . w . CompareTo ( other . w ); } } // Graph class represents a directed graph // using adjacency list representation public class Graph { private int V ; // No. of vertices private List < int > [] adj ; private List < Edge > edges ; public Graph ( int v ) // Constructor { V = v ; adj = new List < int > [ v ]; for ( int i = 0 ; i < v ; i ++ ) adj [ i ] = new List < int > (); edges = new List < Edge > (); } // function to Add an edge public void AddEdge ( int u int v int w ) { adj [ u ]. Add ( v ); // Add w to v’s list. adj [ v ]. Add ( u ); // Add w to v’s list. edges . Add ( new Edge ( u v w )); } // function to perform dfs private void DFS ( int v bool [] visited ) { // Mark the current node as visited and print it visited [ v ] = true ; // Recur for all the vertices adjacent to // this vertex foreach ( int i in adj [ v ]) { if ( ! visited [ i ]) DFS ( i visited ); } } // Returns true if given graph is connected else false private bool IsConnected () { bool [] visited = new bool [ V ]; // Find all reachable vertices from first vertex DFS ( 0 visited ); // If set of reachable vertices includes all // return true. for ( int i = 1 ; i < V ; i ++ ) { if ( visited [ i ] == false ) return false ; } return true ; } // This function assumes that edge (u v) // exists in graph or not public void ReverseDeleteMST () { // Sort edges in increasing order on basis of cost edges . Sort (); int mst_wt = 0 ; // Initialize weight of MST Console . WriteLine ( 'Edges in MST' ); // Iterate through all sorted edges in // decreasing order of weights for ( int i = edges . Count - 1 ; i >= 0 ; i -- ) { int u = edges [ i ]. u ; int v = edges [ i ]. v ; // Remove edge from undirected graph adj [ u ]. Remove ( v ); adj [ v ]. Remove ( u ); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if ( IsConnected () == false ) { adj [ u ]. Add ( v ); adj [ v ]. Add ( u ); // This edge is part of MST Console . WriteLine ( '({0} {1})' u v ); mst_wt += edges [ i ]. w ; } } Console . WriteLine ( 'Total weight of MST is {0}' mst_wt ); } } class GFG { // Driver code static void Main ( string [] args ) { // create the graph given in above figure int V = 9 ; Graph g = new Graph ( V ); // making above shown graph g . AddEdge ( 0 1 4 ); g . AddEdge ( 0 7 8 ); g . AddEdge ( 1 2 8 ); g . AddEdge ( 1 7 11 ); g . AddEdge ( 2 3 7 ); g . AddEdge ( 2 8 2 ); g . AddEdge ( 2 5 4 ); g . AddEdge ( 3 4 9 ); g . AddEdge ( 3 5 14 ); g . AddEdge ( 4 5 10 ); g . AddEdge ( 5 6 2 ); g . AddEdge ( 6 7 1 ); g . AddEdge ( 6 8 6 ); g . AddEdge ( 7 8 7 ); g . ReverseDeleteMST (); } } // This code is contributed by cavi4762
ProduktionEdges in MST (3 4) (0 7) (2 3) (2 5) (0 1) (5 6) (2 8) (6 7) Total weight of MST is 37Tidskompleksitet: O((E*(V+E)) + E log E) hvor E er antallet af kanter.
Rumkompleksitet: O(V+E) hvor V er antallet af hjørner og E er antallet af kanter. Vi bruger tilgrænsende liste til at gemme grafen, så vi har brug for mellemrum proportionalt med O(V+E).
Bemærkninger:
- Ovenstående implementering er en simpel/naiv implementering af Reverse Delete-algoritmen og kan optimeres til O(E log V (log log V) 3 ) [Kilde: En uge ]. Men denne optimerede tidskompleksitet er stadig mindre end Prim og Kruskal Algoritmer til MST.
- Ovenstående implementering ændrer den originale graf. Vi kan lave en kopi af grafen, hvis den originale graf skal bibeholdes.
Opret Quiz