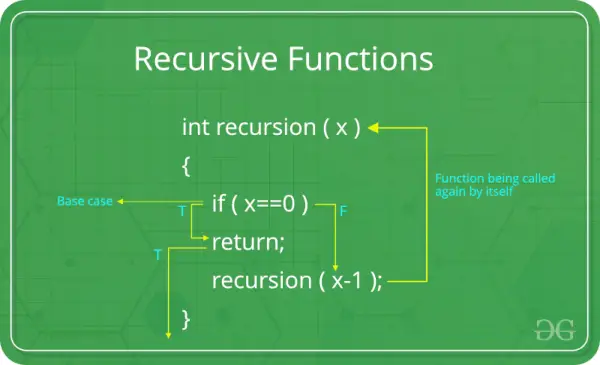
En rekursiv funktion kan defineres som en rutine, der kalder sig selv direkte eller indirekte.

Med andre ord er en rekursiv funktion en funktion, der løser et problem ved at løse mindre forekomster af samme problem. Denne teknik bruges almindeligvis i programmering til at løse problemer, der kan opdeles i enklere, lignende underproblemer.

Behov for rekursiv funktion:

En rekursiv funktion er en funktion, der løser et problem ved at løse mindre forekomster af samme problem. Denne teknik bruges ofte i programmering til at løse problemer, der kan opdeles i enklere, lignende underproblemer.

1. Løsning af komplekse opgaver:

Rekursive funktioner opdeler komplekse problemer i mindre forekomster af det samme problem, hvilket resulterer i kompakt og læsbar kode.

2. Del og hersk:

Rekursive funktioner er velegnede til opdel-og-hersk-algoritmer som f.eks. flette sortering og quicksort, opdeling af problemer i mindre delproblemer, løsning af dem rekursivt og sammenlægning af løsninger med det oprindelige problem.

3. Backtracking :

Rekursiv backtracking er ideel til at udforske og løse problemer som N-Queens og Sudoku.

4. Dynamisk programmering:

Rekursive funktioner løser effektivt dynamiske programmeringsproblemer ved at løse underproblemer og kombinere deres løsninger til en komplet løsning.

5. Træ og grafstrukturer:

Rekursive funktioner er gode til at arbejde med træ- og grafstrukturer, hvilket forenkler traversering og mønstergenkendelsesopgaver .

Sådan skriver du en rekursiv funktion:

Komponenter af en rekursiv funktion:

Base case: Hver rekursiv funktion skal have et basistilfælde. Grundscenariet er det enkleste scenarie, der ikke kræver yderligere rekursion. Dette er en opsigelsesbetingelse, der forhindrer funktionen i at kalde sig selv på ubestemt tid. Uden en ordentlig basiscase kan en rekursiv funktion føre til uendelig rekursion.

Rekursivt tilfælde: I det rekursive tilfælde kalder funktionen sig selv med de modificerede argumenter. Dette er essensen af ​​rekursion - at løse et større problem ved at opdele det i mindre forekomster af det samme problem. Det rekursive tilfælde skal flytte sig tættere på basistilfældet med hver iteration.

Lad os overveje eksemplet med fakultet af tal :

I dette eksempel er grundsagen hvornår n er 0 , og funktionen vender tilbage 1 . Det rekursive tilfælde formerer sig n med resultatet af funktionen kaldet med parameter n – 1 . Processen fortsætter, indtil basissagen er nået.

Det er vigtigt at sikre, at den rekursive funktion har et korrekt basistilfælde, og at de rekursive kald fører til basistilfældet, ellers kan proceduren køre på ubestemt tid, hvilket fører til et stackoverløb (overskrider den tilgængelige hukommelse, der er allokeret til funktionskald).

Nedenfor er implementeringen af ​​factorial af et tal:

#include  using namespace std; // Recursive Function to calculate Factorial of a number int factorial(int n) {  // Base case  if (n == 0) {  return 1;  }  // Recursive case  return n * factorial(n - 1); } // Driver Code int main() {  int n = 4;  cout  < < 'Factorial of '  < < n   < < ' is:'  < < factorial(n);  return 0; } 

import java.util.Scanner; public class Factorial {  // Recursive Function to calculate the factorial of a number  static int factorial(int n) {  // Base case: If n is 0, the factorial is 1.  if (n == 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1);  }  public static void main(String[] args) {  int n = 4;  // Calculate and print the factorial of n.  int result = factorial(n);  System.out.println('Factorial of ' + n + ' is: ' + result);  } } 

# Recursive Function to calculate Factorial of a number def factorial(n): # Base case if n == 0: return 1 # Recursive case return n * factorial(n - 1) # Driver Code if __name__ == '__main__': n = 4 print('Factorial of', n, 'is:', factorial(n)) 

using System; class Program {  // Recursive Function to calculate Factorial of a number  static int Factorial(int n)  {  // Base case  if (n == 0)  {  return 1;  }  // Recursive case  return n * Factorial(n - 1);  }  // Driver Code  static void Main()  {  int n = 4;  Console.WriteLine('Factorial of ' + n + ' is: ' + Factorial(n));  } } 

// Function to calculate the factorial of a number using recursion function factorial(n) {  // Base case: If n is 0, the factorial is 1.  if (n === 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1); } // Main function function main() {  // Given number  let n = 4;  // Calculate the factorial of n.  let result = factorial(n);  // Print the result  console.log('Factorial of ' + n + ' is: ' + result); } // Call the main function main(); 

Factorial of 4 is:24 

Tidskompleksitet: På)
Hjælpeplads: På)