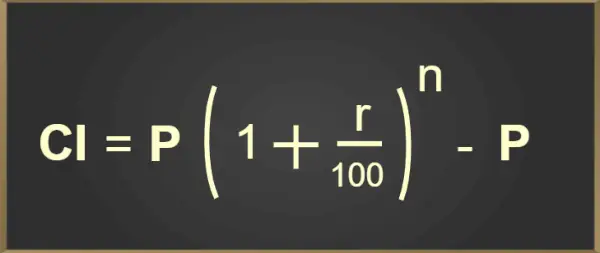Længste efterfølge, sådan at forskellen mellem tilstødende er én


Givet et a rray arr[] af størrelse n opgaven er at finde længste efterfølge sådan at absolut forskel mellem tilstødende elementer er 1.
Eksempler:
Input: arr[] = [10 9 4 5 4 8 6]
Produktion: 3
Forklaring: De tre mulige undersekvenser af længde 3 er [10 9 8] [4 5 4] og [4 5 6], hvor tilstødende elementer har en absolut forskel på 1. Der kunne ikke dannes en gyldig undersekvens af større længde.
Input: arr[] = [1 2 3 4 5]
Produktion: 5
Forklaring: Alle elementerne kan indgå i den gyldige efterfølge.
Brug af rekursion - O(2^n) Tid og O(n) Mellemrum
C++For rekursiv tilgang vi vil overveje to sager ved hvert trin:
- Hvis elementet opfylder betingelsen (den absolut forskel mellem tilstødende elementer er 1) vi omfatte det i efterfølgende og gå videre til næste element.
- ellers vi springe de strøm element og gå videre til det næste.
Matematisk den gentagelsesforhold vil se ud som følgende:
- longestSubseq(arr idx prev) = max(longestSubseq(arr idx + 1 prev) 1 + longestSubseq(arr idx + 1 idx))
Base Case:
- Når idx == arr.size() vi har nået slutningen af arrayet så returnere 0 (da der ikke kan medtages flere elementer).
// C++ program to find the longest subsequence such that // the difference between adjacent elements is one using // recursion. #include using namespace std ; int subseqHelper ( int idx int prev vector < int >& arr ) { // Base case: if index reaches the end of the array if ( idx == arr . size ()) { return 0 ; } // Skip the current element and move to the next index int noTake = subseqHelper ( idx + 1 prev arr ); // Take the current element if the condition is met int take = 0 ; if ( prev == -1 || abs ( arr [ idx ] - arr [ prev ]) == 1 ) { take = 1 + subseqHelper ( idx + 1 idx arr ); } // Return the maximum of the two options return max ( take noTake ); } // Function to find the longest subsequence int longestSubseq ( vector < int >& arr ) { // Start recursion from index 0 // with no previous element return subseqHelper ( 0 -1 arr ); } int main () { vector < int > arr = { 10 9 4 5 4 8 6 }; cout < < longestSubseq ( arr ); return 0 ; }
Java // Java program to find the longest subsequence such that // the difference between adjacent elements is one using // recursion. import java.util.ArrayList ; class GfG { // Helper function to recursively find the subsequence static int subseqHelper ( int idx int prev ArrayList < Integer > arr ) { // Base case: if index reaches the end of the array if ( idx == arr . size ()) { return 0 ; } // Skip the current element and move to the next index int noTake = subseqHelper ( idx + 1 prev arr ); // Take the current element if the condition is met int take = 0 ; if ( prev == - 1 || Math . abs ( arr . get ( idx ) - arr . get ( prev )) == 1 ) { take = 1 + subseqHelper ( idx + 1 idx arr ); } // Return the maximum of the two options return Math . max ( take noTake ); } // Function to find the longest subsequence static int longestSubseq ( ArrayList < Integer > arr ) { // Start recursion from index 0 // with no previous element return subseqHelper ( 0 - 1 arr ); } public static void main ( String [] args ) { ArrayList < Integer > arr = new ArrayList <> (); arr . add ( 10 ); arr . add ( 9 ); arr . add ( 4 ); arr . add ( 5 ); arr . add ( 4 ); arr . add ( 8 ); arr . add ( 6 ); System . out . println ( longestSubseq ( arr )); } }
Python # Python program to find the longest subsequence such that # the difference between adjacent elements is one using # recursion. def subseq_helper ( idx prev arr ): # Base case: if index reaches the end of the array if idx == len ( arr ): return 0 # Skip the current element and move to the next index no_take = subseq_helper ( idx + 1 prev arr ) # Take the current element if the condition is met take = 0 if prev == - 1 or abs ( arr [ idx ] - arr [ prev ]) == 1 : take = 1 + subseq_helper ( idx + 1 idx arr ) # Return the maximum of the two options return max ( take no_take ) def longest_subseq ( arr ): # Start recursion from index 0 # with no previous element return subseq_helper ( 0 - 1 arr ) if __name__ == '__main__' : arr = [ 10 9 4 5 4 8 6 ] print ( longest_subseq ( arr ))
C# // C# program to find the longest subsequence such that // the difference between adjacent elements is one using // recursion. using System ; using System.Collections.Generic ; class GfG { // Helper function to recursively find the subsequence static int SubseqHelper ( int idx int prev List < int > arr ) { // Base case: if index reaches the end of the array if ( idx == arr . Count ) { return 0 ; } // Skip the current element and move to the next index int noTake = SubseqHelper ( idx + 1 prev arr ); // Take the current element if the condition is met int take = 0 ; if ( prev == - 1 || Math . Abs ( arr [ idx ] - arr [ prev ]) == 1 ) { take = 1 + SubseqHelper ( idx + 1 idx arr ); } // Return the maximum of the two options return Math . Max ( take noTake ); } // Function to find the longest subsequence static int LongestSubseq ( List < int > arr ) { // Start recursion from index 0 // with no previous element return SubseqHelper ( 0 - 1 arr ); } static void Main ( string [] args ) { List < int > arr = new List < int > { 10 9 4 5 4 8 6 }; Console . WriteLine ( LongestSubseq ( arr )); } }
JavaScript // JavaScript program to find the longest subsequence // such that the difference between adjacent elements // is one using recursion. function subseqHelper ( idx prev arr ) { // Base case: if index reaches the end of the array if ( idx === arr . length ) { return 0 ; } // Skip the current element and move to the next index let noTake = subseqHelper ( idx + 1 prev arr ); // Take the current element if the condition is met let take = 0 ; if ( prev === - 1 || Math . abs ( arr [ idx ] - arr [ prev ]) === 1 ) { take = 1 + subseqHelper ( idx + 1 idx arr ); } // Return the maximum of the two options return Math . max ( take noTake ); } function longestSubseq ( arr ) { // Start recursion from index 0 // with no previous element return subseqHelper ( 0 - 1 arr ); } const arr = [ 10 9 4 5 4 8 6 ]; console . log ( longestSubseq ( arr ));
Produktion
3
Brug af Top-Down DP (Memoization ) - O(n^2) Tid og O(n^2) Plads
Hvis vi lægger mærke til det, kan vi observere, at ovenstående rekursive løsning har følgende to egenskaber af Dynamisk programmering :
1. Optimal underbygning: Løsningen til at finde den længste efterfølge, sådan at forskel mellem tilstødende elementer kan man udlede af de optimale løsninger af mindre delproblemer. Specifikt for enhver given idx (aktuelt indeks) og forrige (tidligere indeks i efterfølgen) kan vi udtrykke den rekursive relation som følger:
- subseqHelper(idx prev) = max(subseqHelper(idx + 1 prev) 1 + subseqHelper(idx + 1 idx))
2. Overlappende underproblemer: Ved implementering af en rekursive tilgang til at løse problemet, vi observerer, at mange delproblemer beregnes flere gange. For eksempel ved computere subseqHelper(0 -1) for et array arr = [10 9 4 5] underproblemet subseqHelper(2 -1) kan beregnes flere gange. For at undgå denne gentagelse bruger vi memoization til at gemme resultaterne af tidligere beregnede underproblemer.
Den rekursive løsning involverer to parametre:
- idx (det aktuelle indeks i arrayet).
- forrige (indekset for det sidst inkluderede element i efterfølgen).
Vi skal spore begge parametre så vi skaber en 2D array memo af størrelse (n) x (n+1) . Vi initialiserer 2D array memo med -1 for at indikere, at der endnu ikke er beregnet underproblemer. Før vi beregner et resultat, kontrollerer vi, om værdien ved memo[idx][prev+1] er -1. Hvis det er, beregner vi og butik resultatet. Ellers returnerer vi det gemte resultat.
C++ // C++ program to find the longest subsequence such that // the difference between adjacent elements is one using // recursion with memoization. #include using namespace std ; // Helper function to recursively find the subsequence int subseqHelper ( int idx int prev vector < int >& arr vector < vector < int >>& memo ) { // Base case: if index reaches the end of the array if ( idx == arr . size ()) { return 0 ; } // Check if the result is already computed if ( memo [ idx ][ prev + 1 ] != -1 ) { return memo [ idx ][ prev + 1 ]; } // Skip the current element and move to the next index int noTake = subseqHelper ( idx + 1 prev arr memo ); // Take the current element if the condition is met int take = 0 ; if ( prev == -1 || abs ( arr [ idx ] - arr [ prev ]) == 1 ) { take = 1 + subseqHelper ( idx + 1 idx arr memo ); } // Store the result in the memo table return memo [ idx ][ prev + 1 ] = max ( take noTake ); } // Function to find the longest subsequence int longestSubseq ( vector < int >& arr ) { int n = arr . size (); // Create a memoization table initialized to -1 vector < vector < int >> memo ( n vector < int > ( n + 1 -1 )); // Start recursion from index 0 with no previous element return subseqHelper ( 0 -1 arr memo ); } int main () { // Input array of integers vector < int > arr = { 10 9 4 5 4 8 6 }; cout < < longestSubseq ( arr ); return 0 ; }
Java // Java program to find the longest subsequence such that // the difference between adjacent elements is one using // recursion with memoization. import java.util.ArrayList ; import java.util.Arrays ; class GfG { // Helper function to recursively find the subsequence static int subseqHelper ( int idx int prev ArrayList < Integer > arr int [][] memo ) { // Base case: if index reaches the end of the array if ( idx == arr . size ()) { return 0 ; } // Check if the result is already computed if ( memo [ idx ][ prev + 1 ] != - 1 ) { return memo [ idx ][ prev + 1 ] ; } // Skip the current element and move to the next index int noTake = subseqHelper ( idx + 1 prev arr memo ); // Take the current element if the condition is met int take = 0 ; if ( prev == - 1 || Math . abs ( arr . get ( idx ) - arr . get ( prev )) == 1 ) { take = 1 + subseqHelper ( idx + 1 idx arr memo ); } // Store the result in the memo table memo [ idx ][ prev + 1 ] = Math . max ( take noTake ); // Return the stored result return memo [ idx ][ prev + 1 ] ; } // Function to find the longest subsequence static int longestSubseq ( ArrayList < Integer > arr ) { int n = arr . size (); // Create a memoization table initialized to -1 int [][] memo = new int [ n ][ n + 1 ] ; for ( int [] row : memo ) { Arrays . fill ( row - 1 ); } // Start recursion from index 0 // with no previous element return subseqHelper ( 0 - 1 arr memo ); } public static void main ( String [] args ) { ArrayList < Integer > arr = new ArrayList <> (); arr . add ( 10 ); arr . add ( 9 ); arr . add ( 4 ); arr . add ( 5 ); arr . add ( 4 ); arr . add ( 8 ); arr . add ( 6 ); System . out . println ( longestSubseq ( arr )); } }
Python # Python program to find the longest subsequence such that # the difference between adjacent elements is one using # recursion with memoization. def subseq_helper ( idx prev arr memo ): # Base case: if index reaches the end of the array if idx == len ( arr ): return 0 # Check if the result is already computed if memo [ idx ][ prev + 1 ] != - 1 : return memo [ idx ][ prev + 1 ] # Skip the current element and move to the next index no_take = subseq_helper ( idx + 1 prev arr memo ) # Take the current element if the condition is met take = 0 if prev == - 1 or abs ( arr [ idx ] - arr [ prev ]) == 1 : take = 1 + subseq_helper ( idx + 1 idx arr memo ) # Store the result in the memo table memo [ idx ][ prev + 1 ] = max ( take no_take ) # Return the stored result return memo [ idx ][ prev + 1 ] def longest_subseq ( arr ): n = len ( arr ) # Create a memoization table initialized to -1 memo = [[ - 1 for _ in range ( n + 1 )] for _ in range ( n )] # Start recursion from index 0 with # no previous element return subseq_helper ( 0 - 1 arr memo ) if __name__ == '__main__' : arr = [ 10 9 4 5 4 8 6 ] print ( longest_subseq ( arr ))
C# // C# program to find the longest subsequence such that // the difference between adjacent elements is one using // recursion with memoization. using System ; using System.Collections.Generic ; class GfG { // Helper function to recursively find the subsequence static int SubseqHelper ( int idx int prev List < int > arr int [] memo ) { // Base case: if index reaches the end of the array if ( idx == arr . Count ) { return 0 ; } // Check if the result is already computed if ( memo [ idx prev + 1 ] != - 1 ) { return memo [ idx prev + 1 ]; } // Skip the current element and move to the next index int noTake = SubseqHelper ( idx + 1 prev arr memo ); // Take the current element if the condition is met int take = 0 ; if ( prev == - 1 || Math . Abs ( arr [ idx ] - arr [ prev ]) == 1 ) { take = 1 + SubseqHelper ( idx + 1 idx arr memo ); } // Store the result in the memoization table memo [ idx prev + 1 ] = Math . Max ( take noTake ); // Return the stored result return memo [ idx prev + 1 ]; } // Function to find the longest subsequence static int LongestSubseq ( List < int > arr ) { int n = arr . Count ; // Create a memoization table initialized to -1 int [] memo = new int [ n n + 1 ]; for ( int i = 0 ; i < n ; i ++ ) { for ( int j = 0 ; j <= n ; j ++ ) { memo [ i j ] = - 1 ; } } // Start recursion from index 0 with no previous element return SubseqHelper ( 0 - 1 arr memo ); } static void Main ( string [] args ) { List < int > arr = new List < int > { 10 9 4 5 4 8 6 }; Console . WriteLine ( LongestSubseq ( arr )); } }
JavaScript // JavaScript program to find the longest subsequence // such that the difference between adjacent elements // is one using recursion with memoization. function subseqHelper ( idx prev arr memo ) { // Base case: if index reaches the end of the array if ( idx === arr . length ) { return 0 ; } // Check if the result is already computed if ( memo [ idx ][ prev + 1 ] !== - 1 ) { return memo [ idx ][ prev + 1 ]; } // Skip the current element and move to the next index let noTake = subseqHelper ( idx + 1 prev arr memo ); // Take the current element if the condition is met let take = 0 ; if ( prev === - 1 || Math . abs ( arr [ idx ] - arr [ prev ]) === 1 ) { take = 1 + subseqHelper ( idx + 1 idx arr memo ); } // Store the result in the memoization table memo [ idx ][ prev + 1 ] = Math . max ( take noTake ); // Return the stored result return memo [ idx ][ prev + 1 ]; } function longestSubseq ( arr ) { let n = arr . length ; // Create a memoization table initialized to -1 let memo = Array . from ({ length : n } () => Array ( n + 1 ). fill ( - 1 )); // Start recursion from index 0 with no previous element return subseqHelper ( 0 - 1 arr memo ); } const arr = [ 10 9 4 5 4 8 6 ]; console . log ( longestSubseq ( arr ));
Produktion
3
Brug af Bottom-Up DP (Tabulering) - På) Tid og På) Plads
Fremgangsmåden ligner rekursiv metode, men i stedet for at nedbryde problemet rekursivt bygger vi iterativt løsningen i en bottom-up måde.
I stedet for at bruge rekursion bruger vi en hashmap baseret dynamisk programmeringstabel (dp) for at gemme længder af de længste delsekvenser. Dette hjælper os med effektivt at beregne og opdatere efterfølgen længder for alle mulige værdier af array-elementer.
C++Dynamisk programmeringsrelation:
dp[x] repræsenterer længde af den længste undersekvens, der slutter med elementet x.
For hvert element arr[i] i arrayet: Hvis arr[i] + 1 eller arr[i] - 1 findes i dp:
- dp[arr[i]] = 1 + max(dp[arr[i] + 1] dp[arr[i] - 1]);
Det betyder, at vi kan forlænge de delsekvenser, der slutter med arr[i] + 1 eller arr[i] - 1 ved inklusive arr[i].
Ellers start en ny efterfølge:
- dp[arr[i]] = 1;
// C++ program to find the longest subsequence such that // the difference between adjacent elements is one using // Tabulation. #include using namespace std ; int longestSubseq ( vector < int >& arr ) { int n = arr . size (); // Base case: if the array has only // one element if ( n == 1 ) { return 1 ; } // Map to store the length of the longest subsequence unordered_map < int int > dp ; int ans = 1 ; // Loop through the array to fill the map // with subsequence lengths for ( int i = 0 ; i < n ; ++ i ) { // Check if the current element is adjacent // to another subsequence if ( dp . count ( arr [ i ] + 1 ) > 0 || dp . count ( arr [ i ] - 1 ) > 0 ) { dp [ arr [ i ]] = 1 + max ( dp [ arr [ i ] + 1 ] dp [ arr [ i ] - 1 ]); } else { dp [ arr [ i ]] = 1 ; } // Update the result with the maximum // subsequence length ans = max ( ans dp [ arr [ i ]]); } return ans ; } int main () { vector < int > arr = { 10 9 4 5 4 8 6 }; cout < < longestSubseq ( arr ); return 0 ; }
Java // Java code to find the longest subsequence such that // the difference between adjacent elements // is one using Tabulation. import java.util.HashMap ; import java.util.ArrayList ; class GfG { static int longestSubseq ( ArrayList < Integer > arr ) { int n = arr . size (); // Base case: if the array has only one element if ( n == 1 ) { return 1 ; } // Map to store the length of the longest subsequence HashMap < Integer Integer > dp = new HashMap <> (); int ans = 1 ; // Loop through the array to fill the map // with subsequence lengths for ( int i = 0 ; i < n ; ++ i ) { // Check if the current element is adjacent // to another subsequence if ( dp . containsKey ( arr . get ( i ) + 1 ) || dp . containsKey ( arr . get ( i ) - 1 )) { dp . put ( arr . get ( i ) 1 + Math . max ( dp . getOrDefault ( arr . get ( i ) + 1 0 ) dp . getOrDefault ( arr . get ( i ) - 1 0 ))); } else { dp . put ( arr . get ( i ) 1 ); } // Update the result with the maximum // subsequence length ans = Math . max ( ans dp . get ( arr . get ( i ))); } return ans ; } public static void main ( String [] args ) { ArrayList < Integer > arr = new ArrayList <> (); arr . add ( 10 ); arr . add ( 9 ); arr . add ( 4 ); arr . add ( 5 ); arr . add ( 4 ); arr . add ( 8 ); arr . add ( 6 ); System . out . println ( longestSubseq ( arr )); } }
Python # Python code to find the longest subsequence such that # the difference between adjacent elements is # one using Tabulation. def longestSubseq ( arr ): n = len ( arr ) # Base case: if the array has only one element if n == 1 : return 1 # Dictionary to store the length of the # longest subsequence dp = {} ans = 1 for i in range ( n ): # Check if the current element is adjacent to # another subsequence if arr [ i ] + 1 in dp or arr [ i ] - 1 in dp : dp [ arr [ i ]] = 1 + max ( dp . get ( arr [ i ] + 1 0 ) dp . get ( arr [ i ] - 1 0 )) else : dp [ arr [ i ]] = 1 # Update the result with the maximum # subsequence length ans = max ( ans dp [ arr [ i ]]) return ans if __name__ == '__main__' : arr = [ 10 9 4 5 4 8 6 ] print ( longestSubseq ( arr ))
C# // C# code to find the longest subsequence such that // the difference between adjacent elements // is one using Tabulation. using System ; using System.Collections.Generic ; class GfG { static int longestSubseq ( List < int > arr ) { int n = arr . Count ; // Base case: if the array has only one element if ( n == 1 ) { return 1 ; } // Map to store the length of the longest subsequence Dictionary < int int > dp = new Dictionary < int int > (); int ans = 1 ; // Loop through the array to fill the map with // subsequence lengths for ( int i = 0 ; i < n ; ++ i ) { // Check if the current element is adjacent to // another subsequence if ( dp . ContainsKey ( arr [ i ] + 1 ) || dp . ContainsKey ( arr [ i ] - 1 )) { dp [ arr [ i ]] = 1 + Math . Max ( dp . GetValueOrDefault ( arr [ i ] + 1 0 ) dp . GetValueOrDefault ( arr [ i ] - 1 0 )); } else { dp [ arr [ i ]] = 1 ; } // Update the result with the maximum // subsequence length ans = Math . Max ( ans dp [ arr [ i ]]); } return ans ; } static void Main ( string [] args ) { List < int > arr = new List < int > { 10 9 4 5 4 8 6 }; Console . WriteLine ( longestSubseq ( arr )); } }
JavaScript // Function to find the longest subsequence such that // the difference between adjacent elements // is one using Tabulation. function longestSubseq ( arr ) { const n = arr . length ; // Base case: if the array has only one element if ( n === 1 ) { return 1 ; } // Object to store the length of the // longest subsequence let dp = {}; let ans = 1 ; // Loop through the array to fill the object // with subsequence lengths for ( let i = 0 ; i < n ; i ++ ) { // Check if the current element is adjacent to // another subsequence if (( arr [ i ] + 1 ) in dp || ( arr [ i ] - 1 ) in dp ) { dp [ arr [ i ]] = 1 + Math . max ( dp [ arr [ i ] + 1 ] || 0 dp [ arr [ i ] - 1 ] || 0 ); } else { dp [ arr [ i ]] = 1 ; } // Update the result with the maximum // subsequence length ans = Math . max ( ans dp [ arr [ i ]]); } return ans ; } const arr = [ 10 9 4 5 4 8 6 ]; console . log ( longestSubseq ( arr ));
Produktion
3Opret quiz