Komplekse tal i Python | Sæt 1 (introduktion)
Ikke kun reelle tal Python kan også håndtere komplekse tal og dets tilhørende funktioner ved hjælp af filen 'cmath'. Komplekse tal har deres anvendelse i mange applikationer relateret til matematik, og python giver nyttige værktøjer til at håndtere og manipulere dem. Konvertering af reelle tal til komplekse tal Et komplekst tal er repræsenteret ved ' x + yi '. Python konverterer de reelle tal x og y til komplekse ved hjælp af funktionen kompleks(xy) . Den rigtige del kan tilgås ved hjælp af funktionen ægte() og imaginær del kan repræsenteres ved billede() .
Python # Python code to demonstrate the working of # complex() real() and imag() # importing 'cmath' for complex number operations import cmath # Initializing real numbers x = 5 y = 3 # converting x and y into complex number z = complex ( x y ) # printing real and imaginary part of complex number print ( 'The real part of complex number is:' z . real ) print ( 'The imaginary part of complex number is:' z . imag )
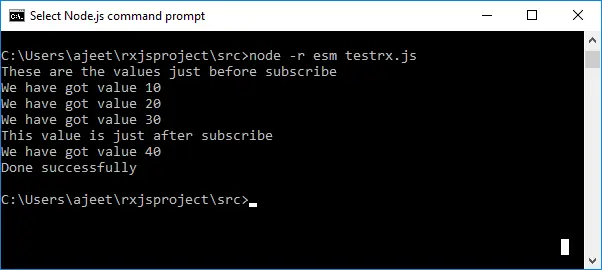
Produktion
The real part of complex number is: 5.0 The imaginary part of complex number is: 3.0
En alternativ måde at initialisere et komplekst tal på
Nedenfor er implementeringen af, hvordan kan vi lave kompleks nr. uden at bruge kompleks() funktion .
Python # An alternative way to initialize complex numbers' # importing 'cmath' for complex number operations import cmath # Initializing complex number z = 5 + 3 j # Print the parts of Complex No. print ( 'The real part of complex number is : ' end = '' ) print ( z . real ) print ( 'The imaginary part of complex number is : ' end = '' ) print ( z . imag )
Produktion
The real part of complex number is : 5.0 The imaginary part of complex number is : 3.0
Forklaring: Fase af komplekst tal Geometrisk er fasen af et komplekst tal vinklen mellem den positive reelle akse og vektoren, der repræsenterer et komplekst tal . Dette er også kendt som argumentet af et komplekst tal. Fase returneres vha fase() som tager et komplekst tal som argument. Rækkevidden af fase ligger fra -pi betyder +pi. dvs fra -3,14 til +3,14 .
Python # importing 'cmath' for complex number operations import cmath # Initializing real numbers x = - 1.0 y = 0.0 # converting x and y into complex number z = complex ( x y ) # printing phase of a complex number using phase() print ( 'The phase of complex number is:' cmath . phase ( z ))
Produktion
The phase of complex number is: 3.141592653589793
Konvertering fra polær til rektangulær form og omvendt Konvertering til polær udføres vha polar() som returnerer en par (rph) betegner modul r og fase vinkel ph . modul kan vises vha abs() og fasebrug fase() . Et komplekst tal konverteres til rektangulære koordinater ved at bruge rect(r ph) hvor r er modul og ph er fasevinklen . Det returnerer en værdi numerisk lig med r * (math.cos(ph) + math.sin(ph)*1j)
Python # importing 'cmath' for complex number operations import cmath import math # Initializing real numbers x = 1.0 y = 1.0 # converting x and y into complex number z = complex ( x y ) # converting complex number into polar using polar() w = cmath . polar ( z ) # printing modulus and argument of polar complex number print ( 'The modulus and argument of polar complex number is:' w ) # converting complex number into rectangular using rect() w = cmath . rect ( 1.4142135623730951 0.7853981633974483 ) # printing rectangular form of complex number print ( 'The rectangular form of complex number is:' w )
Produktion
The modulus and argument of polar complex number is: (1.4142135623730951 0.7853981633974483) The rectangular form of complex number is: (1.0000000000000002+1j)
Komplekse tal i Python | Sæt 2 (vigtige funktioner og konstanter)