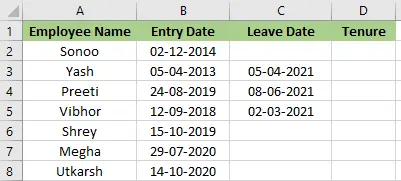
Obrátit pole ve skupinách dané velikosti


Dané pole arr[] a celé číslo k najděte pole po obrácení každého podpole po sobě jdoucích k prvků na místě. Pokud má poslední podpole méně než k prvků, obraťte se tak, jak je. Upravte pole na místě, nic nevrací.
Příklady:
Vstup: arr[] = [1 2 3 4 5 6 7 8] k = 3
výstup: [3 2 1 6 5 4 8 7]
Vysvětlení: Prvky jsou obráceny: [1 2 3] → [3 2 1] [4 5 6] → [6 5 4] a poslední skupina [7 8] (vel. < 3) is reversed as [8 7].Vstup: arr[] = [1 2 3 4 5] k = 3
Výstup: [3 2 1 5 4]
Vysvětlení: První skupinu tvoří prvky 1 2 3. Druhou skupinu tvoří 4 5.já nput: arr[] = [5 6 8 9] k = 5
výstup: [9 8 6 5]
Vysvětlení: Protože k je větší než velikost pole, celé pole je obrácené.
[Přístup ] Obrácení skupiny s pevnou velikostí
Myšlenka je vzít v úvahu každé dílčí pole o velikosti k počínaje od začátku pole a obrátit to. Musíme řešit nějaké speciální případy.
=> Pokud k není násobek n, kde n je velikost pole pro poslední skupinu, zbude nám méně než k prvků, musíme obrátit všechny zbývající prvky.
=> Pokud k = 1, pole by mělo zůstat nezměněno. Je-li k >= n, obrátíme všechny prvky přítomné v poli.Chcete-li obrátit podpole, udržujte dva ukazatele: levý a pravý. Nyní zaměňte prvky na levém a pravém ukazateli a zvyšte levý o 1 a snižte o 1 vpravo. Opakujte, dokud se levý a pravý ukazatel navzájem nekříží.
Pracovní:
C++ #include #include using namespace std ; void reverseInGroups ( vector < int >& arr int k ){ // Get the size of the array int n = arr . size (); for ( int i = 0 ; i < n ; i += k ) { int left = i ; // to handle case when k is not multiple of n int right = min ( i + k - 1 n - 1 ); // reverse the sub-array [left right] while ( left < right ) { swap ( arr [ left ++ ] arr [ right -- ]); } } } int main () { vector < int > arr = { 1 2 3 4 5 6 7 8 }; int k = 3 ; reverseInGroups ( arr k ); for ( int num : arr ) cout < < num < < ' ' ; return 0 ; }
C #include void reverseInGroups ( int arr [] int n int k ){ for ( int i = 0 ; i < n ; i += k ) { int left = i ; int right ; // to handle case when k is not multiple // of n if ( i + k -1 < n -1 ) right = i + k -1 ; else right = n -1 ; // reverse the sub-array [left right] while ( left < right ) { // swap int temp = arr [ left ]; arr [ left ] = arr [ right ]; arr [ right ] = temp ; left ++ ; right -- ; } } } int main () { int arr [] = { 1 2 3 4 5 6 7 8 }; int k = 3 ; int n = sizeof ( arr ) / sizeof ( arr [ 0 ]); reverseInGroups ( arr n k ); for ( int i = 0 ; i < n ; i ++ ) printf ( '%d ' arr [ i ]); return 0 ; }
Java class GfG { static void reverseInGroups ( int [] arr int k ){ int n = arr . length ; for ( int i = 0 ; i < n ; i += k ) { int left = i ; int right = Math . min ( i + k - 1 n - 1 ); // reverse the sub-array while ( left < right ) { int temp = arr [ left ] ; arr [ left ] = arr [ right ] ; arr [ right ] = temp ; left ++ ; right -- ; } } } public static void main ( String [] args ) { int [] arr = { 1 2 3 4 5 6 7 8 }; int k = 3 ; reverseInGroups ( arr k ); for ( int num : arr ) { System . out . print ( num + ' ' ); } } }
Python def reverseInGroups ( arr k ): i = 0 # get the size of the array n = len ( arr ) while i < n : left = i # To handle case when k is not # multiple of n right = min ( i + k - 1 n - 1 ) # reverse the sub-array [left right] while left < right : arr [ left ] arr [ right ] = arr [ right ] arr [ left ] left += 1 right -= 1 i += k if __name__ == '__main__' : arr = [ 1 2 3 4 5 6 7 8 ] k = 3 reverseInGroups ( arr k ) print ( ' ' . join ( map ( str arr )))
C# using System ; class GfG { public static void reverseInGroups ( int [] arr int k ){ int n = arr . Length ; for ( int i = 0 ; i < n ; i += k ) { int left = i ; // to handle case when k is // not multiple of n int right = Math . Min ( i + k - 1 n - 1 ); int temp ; // reverse the sub-array [left right] while ( left < right ) { temp = arr [ left ]; arr [ left ] = arr [ right ]; arr [ right ] = temp ; left += 1 ; right -= 1 ; } } } public static void Main ( string [] args ){ int [] arr = new int [] { 1 2 3 4 5 6 7 8 }; int k = 3 ; int n = arr . Length ; reverseInGroups ( arr k ); for ( int i = 0 ; i < n ; i ++ ) { Console . Write ( arr [ i ] + ' ' ); } } }
JavaScript function reverseInGroups ( arr k ) { let n = arr . length ; for ( let i = 0 ; i < n ; i += k ) { let left = i ; // to handle case when k is not // multiple of n let right = Math . min ( i + k - 1 n - 1 ); // reverse the sub-array [left right] while ( left < right ) { // Swap elements [ arr [ left ] arr [ right ]] = [ arr [ right ] arr [ left ]]; left += 1 ; right -= 1 ; } } return arr ; } // Driver Code let arr = [ 1 2 3 4 5 6 7 8 ]; let k = 3 ; let arr1 = reverseInGroups ( arr k ); console . log ( arr1 . join ( ' ' ));
Výstup
3 2 1 6 5 4 8 7
Časová náročnost: O(n) celé pole projdeme pouze jednou a obrátíme prvky ve skupinách o velikosti k. Protože se nevracíme k žádnému prvku, celková vykonaná práce roste lineárně s velikostí pole. Pokud má tedy pole n prvků, trvá to zhruba n kroků.
Pomocný prostor: O(1) obrácení se provádí přímo v původním poli pomocí několika proměnných navíc.