PROGRAM PYTHON PRO BINÁRNÍ VYHLEDÁVÁNÍ (REKURZIVNÍ A ITERATIVNÍ)

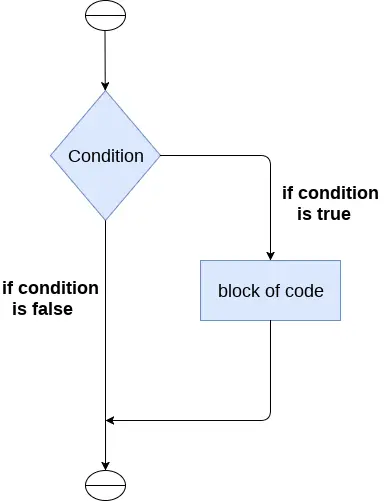
Stručně řečeno, tento vyhledávací algoritmus využívá kolekci prvků, které jsou již setříděny ignorováním poloviny prvků po jediném srovnání.

Porovnejte x se středním prvkem.
Pokud se x shoduje se středním prvkem, vrátíme střední index.
Pokud je x větší než střední prvek, pak x může ležet pouze v pravé (větší) polovině podpole za středním prvkem. Poté znovu použijeme algoritmus pro pravou polovinu.
Pokud je x menší, musí cíl x ležet v levé (spodní) polovině. Aplikujeme tedy algoritmus pro levou polovinu.

Python program pro binární vyhledávání pomocí rekurzivní

Python3

# Python 3 program for recursive binary search.> # Modifications needed for the older Python 2 are found in comments.> # Returns index of x in arr if present, else -1> def> binary_search(arr, low, high, x):> > # Check base case> > if> high>> => low:> > mid> => (high> +> low)> /> /> 2> > # If element is present at the middle itself> > if> arr[mid]> => => x:> > return> mid> > # If element is smaller than mid, then it can only> > # be present in left subarray> > elif> arr[mid]>x:> > return> binary_search(arr, low, mid> -> 1> , x)> > # Else the element can only be present in right subarray> > else> :> > return> binary_search(arr, mid> +> 1> , high, x)> > else> :> > # Element is not present in the array> > return> -> 1> # Test array> arr> => [> 2> ,> 3> ,> 4> ,> 10> ,> 40> ]> x> => 10> # Function call> result> => binary_search(arr,> 0> ,> len> (arr)> -> 1> , x)> if> result !> => -> 1> :> > print> (> 'Element is present at index'> ,> str> (result))> else> :> > print> (> 'Element is not present in array'> )>

Výstup

Element is present at index 3

Časová složitost : O (log n)

Pomocný prostor : O(logn) [POZNÁMKA: Rekurze vytvoří zásobník hovorů]

Program Python pro binární vyhledávání pomocí iterace

Python3

# Iterative Binary Search Function> # It returns index of x in given array arr if present,> # else returns -1> def> binary_search(arr, x):> > low> => 0> > high> => len> (arr)> -> 1> > mid> => 0> > while> low <> => high:> > mid> => (high> +> low)> /> /> 2> > # If x is greater, ignore left half> > if>

arr[mid]   low = mid + 1  # If x is smaller, ignore right half  elif arr[mid]>x: high = mid - 1 # znamená, že x je přítomno uprostřed else: return mid # Pokud se dostaneme sem, pak prvek nebyl přítomen return -1 # Testovací pole arr = [ 2, 3, 4, 10, 40 ] x = 10 # Výsledek volání funkce = binary_search(arr, x) if result != -1: print('Prvek je přítomen na indexu', str(result)) else: print('Prvek není přítomen v poli ')>

Výstup

Element is present at index 3

Časová složitost : O (log n)

Pomocný prostor : O(1)

Program Python pro binární vyhledávání Pomocí vestavěného modulu bisect

Postup krok za krokem:

Kód importuje modul bisect, který poskytuje podporu pro binární vyhledávání.
Je definována funkce binary_search_bisect(), která jako vstupy bere pole arr a prvek pro vyhledávání x.
Funkce volá funkci bisect_left() modulu bisect, která najde pozici prvku v seřazeném poli arr, kam má být vloženo x, aby se zachovalo seřazené pořadí. Pokud je prvek již v poli přítomen, tato funkce vrátí jeho pozici.
Funkce pak zkontroluje, zda je vrácený index i v rozsahu pole a zda je prvek na tomto indexu roven x.
Pokud je podmínka pravdivá, pak funkce vrátí index i jako pozici prvku v poli.
Pokud je podmínka nepravdivá, funkce vrátí hodnotu -1, což znamená, že prvek není v poli přítomen.
Kód pak definuje pole arr a prvek x k vyhledávání.
Funkce binary_search_bisect() se volá s arr a x jako vstupy a vrácený výsledek se uloží do proměnné result.
Kód pak zkontroluje, zda se výsledek nerovná -1, což znamená, že prvek je v poli přítomen. Pokud je true, vytiskne pozici prvku v poli.
Pokud je výsledek roven -1, pak kód vypíše zprávu, že prvek není v poli přítomen.

Python3

import> bisect> > def> binary_search_bisect(arr, x):> > i> => bisect.bisect_left(arr, x)> > if> i !> => len> (arr)> and> arr[i]> => => x:> > return> i> > else> :> > return> -> 1> > > # Test array> arr> => [> 2> ,> 3> ,> 4> ,> 10> ,> 40> ]> x> => 10> > # Function call> result> => binary_search_bisect(arr, x)> > if> result !> => -> 1> :> > print> (> 'Element is present at index'> ,> str> (result))> else> :> > print> (> 'Element is not present in array'> )>

Výstup