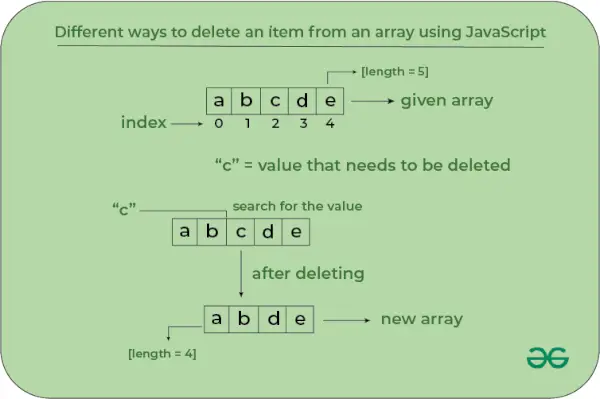
Pozice prvku po stabilním řazení

 #practiceLinkDiv { display: none !important; }
#practiceLinkDiv { display: none !important; } Vzhledem k poli celých čísel, které mohou obsahovat duplicitní prvky, je nám dán prvek tohoto pole, musíme sdělit konečnou pozici tohoto prvku v poli, pokud je aplikován stabilní algoritmus řazení.
Příklady:
Input : arr[] = [3 4 3 5 2 3 4 3 1 5] index = 5 Output : 4 Element initial index – 5 (third 3) After sorting array by stable sorting algorithm we get array as shown below [1(8) 2(4) 3(0) 3(2) 3(5) 3(7) 4(1) 4(6) 5(3) 5(9)] with their initial indices shown in parentheses next to them Element's index after sorting = 4Recommended Practice Stabilní řazení a pozice Zkuste to!
Jeden snadný způsob, jak tento problém vyřešit, je použít jakýkoli stabilní třídicí algoritmus, jako je Řazení vkládání Řazení jde atd a poté získejte nový index daného prvku, ale tento problém můžeme vyřešit bez řazení pole.
O pozici prvku v seřazeném poli rozhodují pouze prvky, které jsou menší než daný prvek. Počítáme všechny prvky pole menší než daný prvek a u těch prvků, které se rovnají daným prvkům prvků, které se vyskytnou před tím, než bude index daného prvku zahrnut do počtu menších prvků, to zajistí stabilitu indexu výsledku.
Jednoduchý kód pro implementaci výše uvedeného přístupu je implementován níže:
C++ // C++ program to get index of array element in // sorted array #include using namespace std ; // Method returns the position of arr[idx] after // performing stable-sort on array int getIndexInSortedArray ( int arr [] int n int idx ) { /* Count of elements smaller than current element plus the equal element occurring before given index*/ int result = 0 ; for ( int i = 0 ; i < n ; i ++ ) { // If element is smaller then increase // the smaller count if ( arr [ i ] < arr [ idx ]) result ++ ; // If element is equal then increase count // only if it occurs before if ( arr [ i ] == arr [ idx ] && i < idx ) result ++ ; } return result ; } // Driver code to test above methods int main () { int arr [] = { 3 4 3 5 2 3 4 3 1 5 }; int n = sizeof ( arr ) / sizeof ( arr [ 0 ]); int idxOfEle = 5 ; cout < < getIndexInSortedArray ( arr n idxOfEle ); return 0 ; }
Java // Java program to get index of array // element in sorted array class ArrayIndex { // Method returns the position of // arr[idx] after performing stable-sort // on array static int getIndexInSortedArray ( int arr [] int n int idx ) { /* Count of elements smaller than current element plus the equal element occurring before given index*/ int result = 0 ; for ( int i = 0 ; i < n ; i ++ ) { // If element is smaller then // increase the smaller count if ( arr [ i ] < arr [ idx ] ) result ++ ; // If element is equal then increase // count only if it occurs before if ( arr [ i ] == arr [ idx ] && i < idx ) result ++ ; } return result ; } // Driver code to test above methods public static void main ( String [] args ) { int arr [] = { 3 4 3 5 2 3 4 3 1 5 }; int n = arr . length ; int idxOfEle = 5 ; System . out . println ( getIndexInSortedArray ( arr n idxOfEle )); } } // This code is contributed by Raghav sharma
Python3 # Python program to get index of array element in # sorted array # Method returns the position of arr[idx] after # performing stable-sort on array def getIndexInSortedArray ( arr n idx ): # Count of elements smaller than current # element plus the equal element occurring # before given index result = 0 for i in range ( n ): # If element is smaller then increase # the smaller count if ( arr [ i ] < arr [ idx ]): result += 1 # If element is equal then increase count # only if it occurs before if ( arr [ i ] == arr [ idx ] and i < idx ): result += 1 return result ; # Driver code to test above methods arr = [ 3 4 3 5 2 3 4 3 1 5 ] n = len ( arr ) idxOfEle = 5 print ( getIndexInSortedArray ( arr n idxOfEle )) # Contributed by: Afzal Ansari
C# // C# program to get index of array // element in sorted array using System ; class ArrayIndex { // Method returns the position of // arr[idx] after performing stable-sort // on array static int getIndexInSortedArray ( int [] arr int n int idx ) { /* Count of elements smaller than current element plus the equal element occurring before given index*/ int result = 0 ; for ( int i = 0 ; i < n ; i ++ ) { // If element is smaller then // increase the smaller count if ( arr [ i ] < arr [ idx ]) result ++ ; // If element is equal then increase // count only if it occurs before if ( arr [ i ] == arr [ idx ] && i < idx ) result ++ ; } return result ; } // Driver code to test above methods public static void Main () { int [] arr = { 3 4 3 5 2 3 4 3 1 5 }; int n = arr . Length ; int idxOfEle = 5 ; Console . WriteLine ( getIndexInSortedArray ( arr n idxOfEle )); } } // This code is contributed by vt_m
PHP // PHP program to get index of // array element in sorted array // Method returns the position of // arr[idx] after performing // stable-sort on array function getIndexInSortedArray ( $arr $n $idx ) { /* Count of elements smaller than current element plus the equal element occurring before given index */ $result = 0 ; for ( $i = 0 ; $i < $n ; $i ++ ) { // If element is smaller then // increase the smaller count if ( $arr [ $i ] < $arr [ $idx ]) $result ++ ; // If element is equal then // increase count only if // it occurs before if ( $arr [ $i ] == $arr [ $idx ] and $i < $idx ) $result ++ ; } return $result ; } // Driver Code $arr = array ( 3 4 3 5 2 3 4 3 1 5 ); $n = count ( $arr ); $idxOfEle = 5 ; echo getIndexInSortedArray ( $arr $n $idxOfEle ); // This code is contributed by anuj_67. ?>
JavaScript < script > // JavaScript program to get index of array // element in sorted array // Method returns the position of // arr[idx] after performing stable-sort // on array function getIndexInSortedArray ( arr n idx ) { /* Count of elements smaller than current element plus the equal element occurring before given index*/ let result = 0 ; for ( let i = 0 ; i < n ; i ++ ) { // If element is smaller then // increase the smaller count if ( arr [ i ] < arr [ idx ]) result ++ ; // If element is equal then increase // count only if it occurs before if ( arr [ i ] == arr [ idx ] && i < idx ) result ++ ; } return result ; } // Driver Code let arr = [ 3 4 3 5 2 3 4 3 1 5 ]; let n = arr . length ; let idxOfEle = 5 ; document . write ( getIndexInSortedArray ( arr n idxOfEle )); // This code is contributed by code_hunt. < /script>
Výstup
4
Časová náročnost: Na) kde n je velikost pole.
Pomocný prostor: O(1)
Vytvořit kvíz