Nejdelší společný podřetězec | DP-29
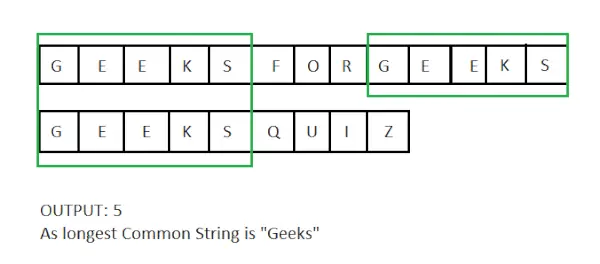
Vzhledem ke dvěma řetězcům ‚X‘ a ‚Y‘ najděte délku nejdelšího společného podřetězce.
Příklady:
Vstup : X = techcodeview.com, y = GeeksQuiz
Výstup : 5
Vysvětlení:
Nejdelší společný podřetězec je Geeks a má délku 5.Vstup : X = abcdxyz, y = xyzabcd
Výstup : 4
Vysvětlení:
Nejdelší společný podřetězec je abcd a má délku 4.Vstup : X = zxabcdezy, y = yzabcdezx
Výstup : 6
Vysvětlení:
Nejdelší společný podřetězec je abcdez a má délku 6.

Přístup:
Nechť m a n jsou délky prvního a druhého řetězce.
A jednoduché řešení je jeden po druhém zohlednit všechny podřetězce prvního řetězce a pro každý podřetězec zkontrolovat, zda se jedná o podřetězec ve druhém řetězci. Sledujte podřetězec maximální délky. Bude zde O(m^2) podřetězců a můžeme zjistit, zda je řetězec podřetězcem na jiném řetězci v čase O(n) (viz tento ). Celková časová složitost této metody by tedy byla O(n * m 2 )
Dynamické programování lze použít k nalezení nejdelšího společného podřetězce v čase O(m*n). Cílem je najít délku nejdelší společné přípony pro všechny podřetězce obou řetězců a uložit tyto délky do tabulky.
Nejdelší společná přípona má následující optimální vlastnost substruktury.
Pokud se poslední znaky shodují, zkrátíme obě délky o 1
- LCSuff(X, Y, m, n) = LCSuff(X, Y, m-1, n-1) + 1, pokud X[m-1] = Y[n-1]
Pokud se poslední znaky neshodují, výsledek je 0, tj.
- LCSuff(X, Y, m, n) = 0 if (X[m-1] != Y[n-1])
Nyní uvažujeme přípony různých podřetězců končících na různých indexech.
Maximální délka Longest Common Sufix je nejdelší společný podřetězec.
LCSubStr(X, Y, m, n) = Max(LCSuff(X, Y, i, j)), kde 1 <= i <= ma 1 <= j <= n
Následuje iterativní implementace výše uvedeného řešení.
C++
/* Dynamic Programming solution to> > find length of the> > longest common substring */> #include> #include> using> namespace> std;> /* Returns length of longest> > common substring of X[0..m-1]> > and Y[0..n-1] */> int> LCSubStr(> char> * X,> char> * Y,> int> m,> int> n)> {> > // Create a table to store> > // lengths of longest> > // common suffixes of substrings.> > // Note that LCSuff[i][j] contains> > // length of longest common suffix> > // of X[0..i-1] and Y[0..j-1].> > int> LCSuff[m + 1][n + 1];> > int> result = 0;> // To store length of the> > // longest common substring> > /* Following steps build LCSuff[m+1][n+1] in> > bottom up fashion. */> > for> (> int> i = 0; i <= m; i++)> > {> > for> (> int> j = 0; j <= n; j++)> > {> > // The first row and first column> > // entries have no logical meaning,> > // they are used only for simplicity> > // of program> > if> (i == 0 || j == 0)> > LCSuff[i][j] = 0;> > else> if> (X[i - 1] == Y[j - 1]) {> > LCSuff[i][j] = LCSuff[i - 1][j - 1] + 1;> > result = max(result, LCSuff[i][j]);> > }> > else> > LCSuff[i][j] = 0;> > }> > }> > return> result;> }> // Driver code> int> main()> {> > char> X[] => 'OldSite:techcodeview.com.org'> ;> > char> Y[] => 'NewSite:GeeksQuiz.com'> ;> > int> m => strlen> (X);> > int> n => strlen> (Y);> > cout < <> 'Length of Longest Common Substring is '> > < < LCSubStr(X, Y, m, n);> > return> 0;> }> |
Jáva
// Java implementation of> // finding length of longest> // Common substring using> // Dynamic Programming> import> java.io.*;> class> GFG {> > /*> > Returns length of longest common substring> > of X[0..m-1] and Y[0..n-1]> > */> > static> int> LCSubStr(> char> X[],> char> Y[],> int> m,> int> n)> > {> > // Create a table to store> > // lengths of longest common> > // suffixes of substrings.> > // Note that LCSuff[i][j]> > // contains length of longest> > // common suffix of> > // X[0..i-1] and Y[0..j-1].> > // The first row and first> > // column entries have no> > // logical meaning, they are> > // used only for simplicity of program> > int> LCStuff[][] => new> int> [m +> 1> ][n +> 1> ];> > // To store length of the longest> > // common substring> > int> result => 0> ;> > // Following steps build> > // LCSuff[m+1][n+1] in bottom up fashion> > for> (> int> i => 0> ; i <= m; i++) {> > for> (> int> j => 0> ; j <= n; j++) {> > if> (i ==> 0> || j ==> 0> )> > LCStuff[i][j] => 0> ;> > else> if> (X[i -> 1> ] == Y[j -> 1> ]) {> > LCStuff[i][j]> > = LCStuff[i -> 1> ][j -> 1> ] +> 1> ;> > result = Integer.max(result,> > LCStuff[i][j]);> > }> > else> > LCStuff[i][j] => 0> ;> > }> > }> > return> result;> > }> > // Driver Code> > public> static> void> main(String[] args)> > {> > String X => 'OldSite:techcodeview.com.org'> ;> > String Y => 'NewSite:GeeksQuiz.com'> ;> > int> m = X.length();> > int> n = Y.length();> > System.out.println(> > 'Length of Longest Common Substring is '> > + LCSubStr(X.toCharArray(), Y.toCharArray(), m,> > n));> > }> }> // This code is contributed by Sumit Ghosh> |
Python3
# Python3 implementation of Finding> # Length of Longest Common Substring> # Returns length of longest common> # substring of X[0..m-1] and Y[0..n-1]> def> LCSubStr(X, Y, m, n):> > # Create a table to store lengths of> > # longest common suffixes of substrings.> > # Note that LCSuff[i][j] contains the> > # length of longest common suffix of> > # X[0...i-1] and Y[0...j-1]. The first> > # row and first column entries have no> > # logical meaning, they are used only> > # for simplicity of the program.> > # LCSuff is the table with zero> > # value initially in each cell> > LCSuff> => [[> 0> for> k> in> range> (n> +> 1> )]> for> l> in> range> (m> +> 1> )]> > # To store the length of> > # longest common substring> > result> => 0> > # Following steps to build> > # LCSuff[m+1][n+1] in bottom up fashion> > for> i> in> range> (m> +> 1> ):> > for> j> in> range> (n> +> 1> ):> > if> (i> => => 0> or> j> => => 0> ):> > LCSuff[i][j]> => 0> > elif> (X[i> -> 1> ]> => => Y[j> -> 1> ]):> > LCSuff[i][j]> => LCSuff[i> -> 1> ][j> -> 1> ]> +> 1> > result> => max> (result, LCSuff[i][j])> > else> :> > LCSuff[i][j]> => 0> > return> result> # Driver Code> X> => 'OldSite:techcodeview.com.org'> Y> => 'NewSite:GeeksQuiz.com'> m> => len> (X)> n> => len> (Y)> print> (> 'Length of Longest Common Substring is'> ,> > LCSubStr(X, Y, m, n))> # This code is contributed by Soumen Ghosh> |
C#
// C# implementation of finding length of longest> // Common substring using Dynamic Programming> using> System;> class> GFG {> > // Returns length of longest common> > // substring of X[0..m-1] and Y[0..n-1]> > static> int> LCSubStr(> string> X,> string> Y,> int> m,> int> n)> > {> > // Create a table to store lengths of> > // longest common suffixes of substrings.> > // Note that LCSuff[i][j] contains length> > // of longest common suffix of X[0..i-1]> > // and Y[0..j-1]. The first row and first> > // column entries have no logical meaning,> > // they are used only for simplicity of> > // program> > int> [, ] LCStuff => new> int> [m + 1, n + 1];> > // To store length of the longest common> > // substring> > int> result = 0;> > // Following steps build LCSuff[m+1][n+1]> > // in bottom up fashion> > for> (> int> i = 0; i <= m; i++)> > {> > for> (> int> j = 0; j <= n; j++)> > {> > if> (i == 0 || j == 0)> > LCStuff[i, j] = 0;> > else> if> (X[i - 1] == Y[j - 1])> > {> > LCStuff[i, j]> > = LCStuff[i - 1, j - 1] + 1;> > result> > = Math.Max(result, LCStuff[i, j]);> > }> > else> > LCStuff[i, j] = 0;> > }> > }> > return> result;> > }> > // Driver Code> > public> static> void> Main()> > {> > String X => 'OldSite:techcodeview.com.org'> ;> > String Y => 'NewSite:GeeksQuiz.com'> ;> > int> m = X.Length;> > int> n = Y.Length;> > Console.Write(> 'Length of Longest Common'> > +> ' Substring is '> > + LCSubStr(X, Y, m, n));> > }> }> // This code is contributed by Sam007.> |
Javascript
> // JavaScript implementation of> // finding length of longest> // Common substring using> // Dynamic Programming> > /*> > Returns length of longest common> > substring of X[0..m-1] and Y[0..n-1]> > */> > function> LCSubStr( X, Y , m , n) {> > // Create a table to store> > // lengths of longest common> > // suffixes of substrings.> > // Note that LCSuff[i][j]> > // contains length of longest> > // common suffix of> > // X[0..i-1] and Y[0..j-1].> > // The first row and first> > // column entries have no> > // logical meaning, they are> > // used only for simplicity of program> > > var> LCStuff => > Array(m + 1).fill().map(()=>Array(n + 1).fill(0));> > // To store length of the longest> > // common substring> > var> result = 0;> > // Following steps build> > // LCSuff[m+1][n+1] in bottom up fashion> > for> (i = 0; i <= m; i++) {> > for> (j = 0; j <= n; j++) {> > if> (i == 0 || j == 0)> > LCStuff[i][j] = 0;> > else> if> (X[i - 1] == Y[j - 1]) {> > LCStuff[i][j] = LCStuff[i - 1][j - 1] + 1;> > result = Math.max(result, LCStuff[i][j]);> > }> else> > LCStuff[i][j] = 0;> > }> > }> > return> result;> > }> > // Driver Code> > > var> X => 'OldSite:techcodeview.com.org'> ;> > var> Y => 'NewSite:GeeksQuiz.com'> ;> > var> m = X.length;> > var> n = Y.length;> > document.write(> 'Length of Longest Common Substring is '> +> > LCSubStr(X, Y, m, n));> // This code contributed by Rajput-Ji> > |
PHP
// Dynamic Programming solution to find // length of the longest common substring // Returns length of longest common // substring of X[0..m-1] and Y[0..n-1] function LCSubStr($X, $Y, $m, $n) { // Create a table to store lengths of // longest common suffixes of substrings. // Notethat LCSuff[i][j] contains length // of longest common suffix of X[0..i-1] // and Y[0..j-1]. The first row and // first column entries have no logical // meaning, they are used only for // simplicity of program $LCSuff = array_fill(0, $m + 1, array_fill(0, $n + 1, NULL)); $result = 0; // To store length of the // longest common substring // Following steps build LCSuff[m+1][n+1] // in bottom up fashion. for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++) { if ($i == 0 || $j == 0) $LCSuff[$i][$j] = 0; else if ($X[$i - 1] == $Y[$j - 1]) { $LCSuff[$i][$j] = $LCSuff[$i - 1][$j - 1] + 1; $result = max($result, $LCSuff[$i][$j]); } else $LCSuff[$i][$j] = 0; } } return $result; } // Driver Code $X = 'OldSite:techcodeview.com.org'; $Y = 'NewSite:GeeksQuiz.com'; $m = strlen($X); $n = strlen($Y); echo 'Length of Longest Common Substring is ' . LCSubStr($X, $Y, $m, $n); // This code is contributed by ita_c ?>> |
Výstup
Length of Longest Common Substring is 10
Časová náročnost: O(m*n)
Pomocný prostor: O(m*n), protože bylo zabráno m*n místa navíc.
Jiný přístup: (Přístup optimalizovaný pro prostor).
Ve výše uvedeném přístupu používáme pouze poslední řádek 2-D pole, proto můžeme optimalizovat prostor pomocí
2-D pole o rozměru 2*(min(n,m)).
Níže je uvedena implementace výše uvedeného přístupu:
C++
#include> #include> using> namespace> std;> // Function to find the length of the longest LCS> int> LCSubStr(string s, string t,> int> n,> int> m)> {> > // Create DP table> > vectorint>> dp(n + 1, vektor |
Jáva
// Java implementation of the above approach> import> java.io.*;> class> GFG> {> > > // Function to find the length of the> > // longest LCS> > static> int> LCSubStr(String s,String t,> > int> n,> int> m)> > {> > > // Create DP table> > int> dp[][]=> new> int> [> 2> ][m+> 1> ];> > int> res=> 0> ;> > > for> (> int> i=> 1> ;i <=n;i++)> > {> > for> (> int> j=> 1> ;j <=m;j++)> > {> > if> (s.charAt(i-> 1> )==t.charAt(j-> 1> ))> > {> > dp[i%> 2> ][j]=dp[(i-> 1> )%> 2> ][j-> 1> ]+> 1> ;> > if> (dp[i%> 2> ][j]>res)> > res=dp[i%> 2> ][j];> > }> > else> dp[i%> 2> ][j]=> 0> ;> > }> > }> > return> res;> > }> > > // Driver Code> > public> static> void> main (String[] args)> > {> > String X=> 'OldSite:techcodeview.com.org'> ;> > String Y=> 'NewSite:GeeksQuiz.com'> ;> > > int> m=X.length();> > int> n=Y.length();> > > // Function call> > System.out.println(LCSubStr(X,Y,m,n));> > > }> }> |
Python3
# Python implementation of the above approach> # Function to find the length of the> # longest LCS> def> LCSubStr(s, t, n, m):> > > # Create DP table> > dp> => [[> 0> for> i> in> range> (m> +> 1> )]> for> j> in> range> (> 2> )]> > res> => 0> > > for> i> in> range> (> 1> ,n> +> 1> ):> > for> j> in> range> (> 1> ,m> +> 1> ):> > if> (s[i> -> 1> ]> => => t[j> -> 1> ]):> > dp[i> %> 2> ][j]> => dp[(i> -> 1> )> %> 2> ][j> -> 1> ]> +> 1> > if> (dp[i> %> 2> ][j]>res):> > res> => dp[i> %> 2> ][j]> > else> :> > dp[i> %> 2> ][j]> => 0> > return> res> # Driver Code> X> => 'OldSite:techcodeview.com.org'> Y> => 'NewSite:GeeksQuiz.com'> m> => len> (X)> n> => len> (Y)> # Function call> print> (LCSubStr(X,Y,m,n))> # This code is contributed by avanitrachhadiya2155> |
C#
// C# implementation of the above approach> using> System;> public> class> GFG> {> > // Function to find the length of the> > // longest LCS> > static> int> LCSubStr(> string> s,> string> t,> > int> n,> int> m)> > {> > // Create DP table> > int> [,] dp => new> int> [2, m + 1];> > int> res = 0;> > for> (> int> i = 1; i <= n; i++)> > {> > for> (> int> j = 1; j <= m; j++)> > {> > if> (s[i - 1] == t[j - 1])> > {> > dp[i % 2, j] = dp[(i - 1) % 2, j - 1] + 1;> > if> (dp[i % 2, j]>res)> > res = dp[i % 2, j];> > }> > else> dp[i % 2, j] = 0;> > }> > }> > return> res;> > }> > // Driver Code> > static> public> void> Main (){> > string> X => 'OldSite:techcodeview.com.org'> ;> > string> Y => 'NewSite:GeeksQuiz.com'> ;> > int> m = X.Length;> > int> n = Y.Length;> > // Function call> > Console.WriteLine(LCSubStr(X,Y,m,n));> > }> }> // This code is contributed by rag2127> |
Javascript
> // JavaScript implementation of the above approach> > // Function to find the length of the> > // longest LCS> > function> LCSubStr(s, t, n, m)> > {> > > // Create DP table> > var> dp = Array(2).fill().map(()=>Pole(m+ 1).fill(0));> > var> res = 0;> > > for> (> var> i = 1; i <= n; i++)> > {> > for> (> var> j = 1; j <= m; j++)> > {> > if> (s.charAt(i - 1) == t.charAt(j - 1))> > {> > dp[i % 2][j] = dp[(i - 1) % 2][j - 1] + 1;> > if> (dp[i % 2][j]>res)> > res = dp[i % 2][j];> > }> > else> dp[i % 2][j] = 0;> > }> > }> > return> res;> > }> > > // Driver Code> > var> X => 'OldSite:techcodeview.com.org'> ;> > var> Y => 'NewSite:GeeksQuiz.com'> ;> > > var> m = X.length;> > var> n = Y.length;> > > // Function call> > document.write(LCSubStr(X, Y, m, n));> // This code is contributed by shivanisinghss2110> > |
Výstup
10
Časová náročnost: O(n*m)
Pomocný prostor: O(min(m,n))
Jiný přístup: (Pomocí rekurze)
Zde je rekurzivní řešení výše uvedeného přístupu.
C++
// C++ program using to find length of the> // longest common substring recursion> #include> using> namespace> std;> string X, Y;> // Returns length of function f> // or longest common substring> // of X[0..m-1] and Y[0..n-1]> int> lcs(> int> i,> int> j,> int> count)> {> > if> (i == 0 || j == 0)> > return> count;> > if> (X[i - 1] == Y[j - 1]) {> > count = lcs(i - 1, j - 1, count + 1);> > }> > count = max(count,> > max(lcs(i, j - 1, 0),> > lcs(i - 1, j, 0)));> > return> count;> }> // Driver code> int> main()> {> > int> n, m;> > X => 'abcdxyz'> ;> > Y => 'xyzabcd'> ;> > n = X.size();> > m = Y.size();> > cout < < lcs(n, m, 0);> > return> 0;> }> |
Jáva
// Java program using to find length of the> // longest common substring recursion> import> java.io.*;> class> GFG {> > static> String X, Y;> > // Returns length of function> > // for longest common> > // substring of X[0..m-1] and Y[0..n-1]> > static> int> lcs(> int> i,> int> j,> int> count)> > {> > if> (i ==> 0> || j ==> 0> )> > {> > return> count;> > }> > if> (X.charAt(i -> 1> )> > == Y.charAt(j -> 1> ))> > {> > count = lcs(i -> 1> , j -> 1> , count +> 1> );> > }> > count = Math.max(count,> > Math.max(lcs(i, j -> 1> ,> 0> ),> > lcs(i -> 1> , j,> 0> )));> > return> count;> > }> > > // Driver code> > public> static> void> main(String[] args)> > {> > int> n, m;> > X => 'abcdxyz'> ;> > Y => 'xyzabcd'> ;> > n = X.length();> > m = Y.length();> > System.out.println(lcs(n, m,> 0> ));> > }> }> // This code is contributed by Rajput-JI> |
Python3
# Python3 program using to find length of> # the longest common substring recursion> # Returns length of function for longest> # common substring of X[0..m-1] and Y[0..n-1]> def> lcs(i, j, count):> > if> (i> => => 0> or> j> => => 0> ):> > return> count> > if> (X[i> -> 1> ]> => => Y[j> -> 1> ]):> > count> => lcs(i> -> 1> , j> -> 1> , count> +> 1> )> > count> => max> (count,> max> (lcs(i, j> -> 1> ,> 0> ),> > lcs(i> -> 1> , j,> 0> )))> > return> count> # Driver code> if> __name__> => => '__main__'> :> > X> => 'abcdxyz'> > Y> => 'xyzabcd'> > n> => len> (X)> > m> => len> (Y)> > print> (lcs(n, m,> 0> ))> # This code is contributed by Ryuga> |
C#
// C# program using to find length> // of the longest common substring> // recursion> using> System;> class> GFG {> > static> String X, Y;> > // Returns length of function for> > // longest common substring of> > // X[0..m-1] and Y[0..n-1]> > static> int> lcs(> int> i,> int> j,> int> count)> > {> > if> (i == 0 || j == 0) {> > return> count;> > }> > if> (X[i - 1] == Y[j - 1]) {> > count = lcs(i - 1, j - 1, count + 1);> > }> > count = Math.Max(count, Math.Max(lcs(i, j - 1, 0),> > lcs(i - 1, j, 0)));> > return> count;> > }> > // Driver code> > public> static> void> Main()> > {> > int> n, m;> > X => 'abcdxyz'> ;> > Y => 'xyzabcd'> ;> > n = X.Length;> > m = Y.Length;> > Console.Write(lcs(n, m, 0));> > }> }> // This code is contributed by Rajput-JI> |
Javascript
> > // Javascript program using to find length of the> > // longest common substring recursion> > let X, Y;> > > // Returns length of function f> > // or longest common substring> > // of X[0..m-1] and Y[0..n-1]> > function> lcs(i, j, count)> > {> > > if> (i == 0 || j == 0)> > return> count;> > > if> (X[i - 1] == Y[j - 1]) {> > count = lcs(i - 1, j - 1, count + 1);> > }> > count = Math.max(count,> > Math.max(lcs(i, j - 1, 0),> > lcs(i - 1, j, 0)));> > return> count;> > }> > > let n, m;> > > X => 'abcdxyz'> ;> > Y => 'xyzabcd'> ;> > > n = X.length;> > m = Y.length;> > > document.write(lcs(n, m, 0));> > > // This code is contributed by divyeshrabadiya07.> > |
PHP
// PHP program using to find length of the // longest common substring recursion // Returns length of function for // longest common substring of // X[0..m-1] and Y[0..n-1] function lcs($i, $j, $count, &$X, &$Y) { if ($i == 0 || $j == 0) return $count; if ($X[$i - 1] == $Y[$j - 1]) { $count = lcs($i - 1, $j - 1, $count + 1, $X, $Y); } $count = max($count, lcs($i, $j - 1, 0, $X, $Y), lcs($i - 1, $j, 0, $X, $Y)); return $count; } // Driver code $X = 'abcdxyz'; $Y = 'xyzabcd'; $n = strlen($X); $m = strlen($Y); echo lcs($n, $m, 0, $X, $Y); // This code is contributed // by rathbhupendra ?>> |
Výstup
4
Časová složitost : O(2^max(m,n)) protože funkce provádí dvě rekurzivní volání – lcs(i, j-1, 0) a lcs(i-1, j, 0), když znaky na X[i-1] != Y[j-1]. Takže to dá nejhorší případ časovou složitost jako 2^N, kde N = max(m, n), ma n je délka řetězce X a Y.
Pomocný prostor: O(1): protože volání funkce nepoužívá žádný prostor navíc (funkce pouze používá zásobník rekurzivního volání, který obecně v pomocném prostoru neuvažujeme).