Algebraické pojmy jako a na rozdíl od nich: definice a příklady
Podobné termíny jsou termíny v algebraických výrazech, které mají stejné proměnné umocněné na stejnou mocninu. Pojmy jako a na rozdíl od nich jsou typy termínů v algebře a můžeme rozlišovat mezi termíny podobnými a odlišnými tím, že jednoduše zkontrolujeme proměnné a jejich pravomoci. Algebraické členy definujeme jako jednotlivé členy získané z algebraické rovnice.

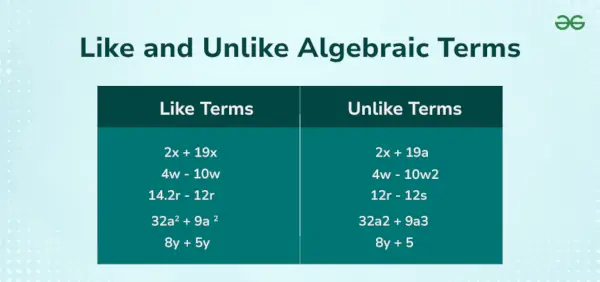
Například v algebraické rovnici 5x + 3 roky 2 = 12 máme tři termíny, 5x, 3y², a 12 . Tady, 5x, a 3r 2 jsou proměnné členy a 12 je konstantní člen. Níže uvedený obrázek ukazuje podobné a odlišné výrazy.
V tomto článku se podrobně seznámíme s výrazy Like, Different Terms, jejich příklady, zjednodušení a další.
Jako Podmínky
Podobné termíny jsou termíny, které mají stejné proměnné a síla každé z proměnných je také stejná. Můžeme kombinovat podobné pojmy, abychom zjednodušili algebraické výrazy, a to lze velmi snadno vypočítat. Například 3y + 5y je algebraický výraz s podobnými pojmy 3y a 5y. Abychom tento algebraický výraz zjednodušili, přidáme podobné výrazy. Zjednodušení daného výrazu je tedy 8y.
Příklady podobných výrazů
Jako termíny jsou termíny, které mají stejnou proměnnou s podobnou mocností. Některé příklady podobných výrazů jsou např.
- 40xy 2 a 56xy 2 : V prvním příkladu xy 2 je společný koeficient pro oba členy. Jsou to tedy jako pojmy.
- 30z 2 a 18z 2 : S 2 je společný koeficient pro oba členy. Jsou to tedy jako pojmy.
- 45abc a 29abc: abc je společný koeficient pro oba členy. Jsou to tedy jako pojmy.
- 18r 3 a 38r 3 : r 3 je společný koeficient pro oba členy. Jsou to tedy jako pojmy.
- 2xy a 8xy: xy je společný koeficient pro oba členy. Jsou to tedy jako pojmy.
Sčítání a odečítání podobných výrazů
Můžeme snadno provádět sčítání a odčítání podobných výrazů a nevyžaduje to žádné zvláštní pravidlo, obecně se zjednodušují pomocí běžných pravidel sčítání a odčítání. Tento koncept můžeme pochopit pomocí následujícího příkladu.
Příklad: Zjednodušte 11x 3 + 5x 3
Řešení:
Jak vidíme, jsou jako termín, protože mají podobné proměnné a jejich síla je také konstantní.
Tyto termíny můžeme snadno přidat přímo.
= 11x 3 + 5x 3
= 16x 3
To je možné, protože mají stejné proměnné s podobnou mocí a to lze chápat tak, že můžeme přímo přidat rupie k rupiím, tj. 5 Rs + 7 Rs je 12 Rs. Ale nemůžeme přímo přidat rupie s dolary a 5 Rs + 7 dolarů nelze přímo zjednodušit.
Podobně můžeme také odečítat podobné termíny přímo, stačí přidat a přidat podobné termíny, což lze pochopit na následujícím příkladu.
Příklad 1: Zjednodušte 11x 3 – 5x 3
Řešení:
Jak vidíme, jsou jako termín, protože mají podobné proměnné a jejich síla je také konstantní.
Tyto pojmy můžeme snadno přímo odečíst.
= 11x 3 – 5x 3
= 6x 3
Příklad 2: Přidejte 3 X + 2 a + 5 a 4 X − 3 a + 7.
Řešení:
(3 X + 2 a + 5) + (4 X − 3 a + 7)
= (3 X + 4x) +(2y + (-3y))+ (5 + 7)
= 7 X − a + 12
Na rozdíl od Podmínek
Na rozdíl od Termínů jsou termíny s různými proměnnými a každá z proměnných může, ale nemusí mít různé exponenty. Například 9x + 6y je algebraický výraz s na rozdíl od termínů. Protože má dvě různé proměnné x a y.
Pokud jsou proměnné různé, nekontrolujeme mocninu, protože se v žádném případě neliší od členů, ale pokud jsou proměnné stejné, kontrolujeme jejich mocniny, protože se mohou, ale nemusí podobat členům.
Třeba 5x 2 a 6x 2 jsou jako termíny, ale 5x 2 a 6x 3 jsou odlišné od termínů.
Příklady výrazů na rozdíl od výrazů
Na rozdíl od termínů jsou termíny, které nemají stejné proměnné ani podobnou moc. Některé příklady odlišných výrazů jsou např.
- 40xy 2 a 56xy: Zde je v jednom algebraickém výrazu proměnná xy 2 a v druhém algebraickém výrazu je proměnná xy. Obě proměnné jsou stejné, ale mají různé síly. Jsou tedy na rozdíl od termínů.
- 45abc a 29ab: Zde je v jednom algebraickém výrazu proměnná abc a v druhém algebraickém výrazu je proměnná ab. Obě proměnné jsou odlišné. Na rozdíl od pojmů tedy spadají do kategorie.
Sčítání a odečítání odlišných pojmů
Sčítání a odčítání se na rozdíl od termínů neprovádí, tj. nemůžeme sčítat ani odečítat rozdílné termíny a to lze pochopit na příkladu, že k 6 kg rýže nemůžeme přidat 5 litrů mléka. Stejně tak nemůžeme na rozdíl od pojmů sčítat ani odečítat.
Například 3xy + 5x nelze dále řešit a je ponecháno stejným způsobem.
Rozdíl mezi výrazy „Líbí se“ a „Na rozdíl od nich“.
Rozdíly mezi podobnými a odlišnými výrazy jsou popsány v tabulce níže.
| Vlastnosti | Jako Podmínky | Na rozdíl od Podmínek |
|---|---|---|
| Definice | Podobné termíny jsou termíny, které mají stejné proměnné a stejné hodnoty exponentů. | Na rozdíl od termínů jsou termíny, které mají různé proměnné a exponenty. |
| Zjednodušení | Podobné termíny můžeme snadno zjednodušit. | Na rozdíl od termínů, které nelze zjednodušit. |
| Kombinování pojmů | Podobné výrazy lze přímo kombinovat a provést výpočet. | Na rozdíl od výrazů nelze přímo kombinovat, protože představují různé veličiny |
| Sčítání nebo odčítání | Sčítání a odčítání lze dosáhnout pomocí podobných podmínek. | Na rozdíl od výrazů nemůžeme sčítat ani odečítat. |
| Příklady | Příklady podobných výrazů jsou x 2 , 5x 2 , -11/3x 2 , atd. | Příklady výrazů Na rozdíl od nich jsou x 2 a 5x 3 , -11/3x atd. |
Přečtěte si více
- Algebraické výrazy
- Typy algebraických výrazů
Příklady algebraických pojmů Líbí a Ne
Příklad 1: Identifikujte podobné a odlišné výrazy z: 3x, 5xy, 18x 2 a 5x 3 , 29xy, 50x 3
Řešení:
Výrazy Like a Na rozdíl od daných výrazů jsou,
Líbí se mi podmínky: (5xy, 29xy) a (5x 3 , 50x 3 )
Na rozdíl od podmínek: 3x, 18x 2 a
Příklad 2: Zjednodušte 3xy + 5x 2 + 11ab – 4xy
Řešení:
Daný výraz: 3xy + 5x 2 + 11ab – 4xy
Stejně jako výraz v daném výrazu, 3xy a -4xy
Na zjednodušení,
= 3xy – 4xy + 5x 2 + 11ab
= -xy + 5x 2 + 11ab
Všechny termíny jsou odlišné od termínů, takže je nelze dále řešit.
Příklad 3: Zjednodušte 8x + 15x 2 + 11x – 4x 2
Řešení:
Daný výraz: 8x + 15x 2 + 11x – 4x 2
Jako výraz v daném výrazu, (8x, 11x) a (15x 2 , -4x 2 )
Na zjednodušení,
= 8x + 11x + 15x 2 – 4x 2
= 19x – 11x 2
Všechny termíny jsou odlišné od termínů, takže je nelze dále řešit.
Algebraické termíny Líbí se a na rozdíl od nich – často kladené dotazy
Co jsou algebraické termíny?
Algebraické členy jsou jednotlivé členy získané z algebraické rovnice, tj. členy dělené operačními symboly jako + a -.
Co jsou to podobné a nepodobné podmínky?
Stejné a odlišné termíny jsou termíny algebraického výrazu. Stejně jako máme podobné proměnné a síla exponentu je stejná, zatímco v odlišných termínech jsou proměnné a jejich síla různé.
Jaký je rozdíl mezi podobnými a odlišnými algebraickými termíny?
Základní rozdíl mezi podobnými a nepodobnými termíny je v tom, že v podobném termínu máme stejnou proměnnou se stejnými pravomocemi, zatímco na rozdíl od podmínek máme různé proměnné s různými pravomocemi.
Jak najít algebraické výrazy Líbí a Ne?
Podobné termíny jsou termíny, které mají stejné proměnné se stejnými pravomocemi, a rozdílné termíny jsou termíny s různými proměnnými a různými pravomocemi a můžeme je snadno identifikovat pouhým prozkoumáním proměnných.
Můžeme sčítat nebo odečítat jako algebraické výrazy?
Můžeme snadno sčítat nebo odečítat, jako jsou výrazy jako 5x a 11x jako výrazy a lze je přidat jako 16x.
Můžeme sčítat nebo odečítat na rozdíl od algebraických termínů?
Na rozdíl od výrazů jako 2x a 3y nemůžeme sčítat ani odečítat. Na rozdíl od výrazů tedy nelze sčítat ani odečítat dohromady.