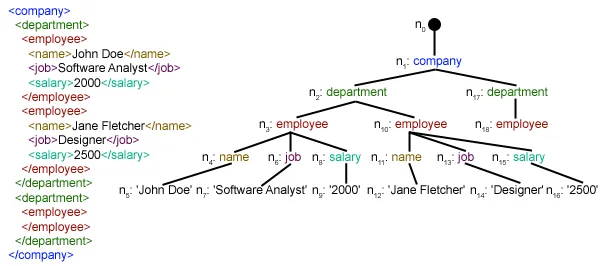
Dekodér

Kombinační obvod, který mění binární informace na 2 N výstupní linky jsou známé jako Dekodéry. Binární informace je předávána ve formě N vstupních řádků. Výstupní řádky definují 2 N -bitový kód pro binární informace. Jednoduše řečeno, Dekodér provádí opačnou operaci Kodér . Pro zjednodušení je vždy aktivován pouze jeden vstupní řádek. Vyrobeno 2 N -bitový výstupní kód je ekvivalentní binární informaci.

Existují různé typy dekodérů, které jsou následující:
2 až 4 řádkový dekodér:
Ve 2 až 4 řádkovém dekodéru jsou celkem tři vstupy, tedy A 0 a A 1 a E a čtyři výstupy, tj. Y 0 , A 1 , A 2 a Y 3 . Pro každou kombinaci vstupů, když je povolení 'E' nastaveno na 1, bude jeden z těchto čtyř výstupů 1. Blokové schéma a pravdivostní tabulka 2 až 4 řádkového dekodéru jsou uvedeny níže.
Blokové schéma:

Tabulka pravdy:

Logické vyjádření výrazů Y0, Y0, Y2 a Y3 je následující:
A 3 = E.A 1 .A 0
A 2 = E.A 1 .A 0 '
A 1 = E.A 1 '.A 0
Y0=E.A 1 '.A 0 '
Logický obvod výše uvedených výrazů je uveden níže:

3 až 8 řádkový dekodér:
3 až 8 řádkový dekodér je také známý jako Binární až osmičkový dekodér . V 3 až 8 řádkovém dekodéru je celkem osm výstupů, tedy Y 0 , A 1 , A 2 , A 3 , A 4 , A 5 , A 6 a Y 7 a tři výstupy, tj 0 , A1 a A 2 . Tento obvod má povolovací vstup „E“. Stejně jako u 2 až 4řádkového dekodéru, když je povoleno 'E' nastaveno na 1, jeden z těchto čtyř výstupů bude 1. Blokové schéma a pravdivostní tabulka 3 až 8řádkového kodéru jsou uvedeny níže.
Blokové schéma:

Tabulka pravdy:

Logické vyjádření termínu Y 0 , A 1 , A 2 , A 3 , A 4 , A 5 , A 6 a Y 7 je následující:
A 0 =A 0 '.A 1 '.A 2 '
A 1 =A 0 .A 1 '.A 2 '
A 2 =A 0 '.A 1 .A 2 '
A 3 =A 0 .A 1 .A 2 '
A 4 =A 0 '.A 1 '.A 2
A 5 =A 0 .A 1 '.A 2
A 6 =A 0 '.A 1 .A 2
A 7 =A 0 .A 1 .A 2
Logický obvod výše uvedených výrazů je uveden níže:

4 až 16 řádkový dekodér
V dekodéru 4 až 16 řádků je celkem 16 výstupů, tj. 0 , A 1 , A 2 ,……, A 16 a čtyři vstupy, tj 0 , A1, A 2 a A 3 . 3 až 16 řádkový dekodér lze zkonstruovat pomocí buď 2 až 4 dekodéru nebo 3 až 8 dekodéru. K nalezení požadovaného počtu dekodérů nižšího řádu se používá následující vzorec.
Požadovaný počet dekodérů nižšího řádu=m 2 /m 1
m 1 = 8
m 2 = 16
Požadovaný počet 3 až 8 dekodérů=  =2
=2
Blokové schéma:

Tabulka pravdy:

Logické vyjádření výrazu A0, A1, A2,…, A15 je následující:
A 0 =A 0 '.A 1 '.A 2 '.A 3 '
A 1 =A 0 '.A 1 '.A 2 '.A 3
A 2 =A 0 '.A 1 '.A 2 .A 3 '
A 3 =A 0 '.A 1 '.A 2 .A 3
A 4 =A 0 '.A 1 .A 2 '.A 3 '
A 5 =A 0 '.A 1 .A 2 '.A 3
A 6 =A 0 '.A 1 .A 2 .A 3 '
A 7 =A 0 '.A 1 .A 2 .A 3
A 8 =A 0 .A 1 '.A 2 '.A 3 '
A 9 =A 0 .A 1 '.A 2 '.A 3
A 10 =A 0 .A 1 '.A 2 .A 3 '
A jedenáct =A 0 .A 1 '.A 2 .A 3
A 12 =A 0 .A 1 .A 2 '.A 3 '
A 13 =A 0 .A 1 .A 2 '.A 3
A 14 =A 0 .A 1 .A 2 .A 3 '
A patnáct =A 0 .A 1 .A 2 '.A 3
Logický obvod výše uvedených výrazů je uveden níže: