Passos mínims per arribar a l'objectiu d'un cavaller | Set 2

Donat un tauler d'escacs quadrat de mida N x N, es dóna la posició del cavaller i la posició d'un objectiu, la tasca és esbrinar els passos mínims que farà un cavaller per arribar a la posició objectiu.

Exemples:
Input : (2 4) - knight's position (6 4) - target cell Output : 2 Input : (4 5) (1 1) Output : 3
Un enfocament de BFS per resoldre el problema anterior ja s'ha discutit al document anterior publicació. En aquesta entrada es parla d'una solució de programació dinàmica.
Explicació de l'enfocament:
Deixeu un tauler d'escacs de 8 x 8 cel·les. Ara diguem que el cavaller és a (3 3) i l'objectiu és a (7 8). Hi ha 8 moviments possibles des de la posició actual de cavaller, és a dir, (2 1) (1 2) (4 1) (1 4) (5 2) (2 5) (5 4) (4 5). Però entre aquests només dos moviments (5 4) i (4 5) seran cap a l'objectiu i tots els altres s'allunyen de l'objectiu. Per tant, per trobar els passos mínims, aneu a (4 5) o (5 4). Ara calculeu els passos mínims fets des de (4 5) i (5 4) per arribar a l'objectiu. Això es calcula mitjançant programació dinàmica. Així, això resulta en els passos mínims de (3 3) a (7 8).
Deixeu un tauler d'escacs de 8 x 8 cel·les. Ara suposem que el cavaller és a (4 3) i l'objectiu és a (4 7). Hi ha 8 moviments possibles, però cap a l'objectiu només hi ha 4 moviments, és a dir (5 5) (3 5) (2 4) (6 4). Com que (5 5) és equivalent a (3 5) i (2 4) és equivalent a (6 4). Així que d'aquests 4 punts es pot convertir en 2 punts. Prenent (5 5) i (6 4) (aquí). Ara calculeu els passos mínims fets a partir d'aquests dos punts per arribar a l'objectiu. Això es calcula mitjançant programació dinàmica. Així, això resulta en els passos mínims de (4 3) a (4 7).
Excepció: Quan el cavaller estarà a la cantonada i l'objectiu és tal que la diferència de coordenades x i y amb la posició del cavaller és (1 1) o viceversa. Aleshores els passos mínims seran 4.
Equació de programació dinàmica:
1) dp[diffOfX][diffOfY] són els passos mínims fets des de la posició del cavaller fins a la posició de l'objectiu.
2) dp[diffOfX][diffOfY] = dp[diffOfY][diffOfX] .
on diffOfX = diferència entre la coordenada x de Knight i la coordenada x de l'objectiu
diffOfY = diferència entre la coordenada y de Knight i la coordenada y de l'objectiu
A continuació es mostra la implementació de l'enfocament anterior:
// C++ code for minimum steps for // a knight to reach target position #include using namespace std ; // initializing the matrix. int dp [ 8 ][ 8 ] = { 0 }; int getsteps ( int x int y int tx int ty ) { // if knight is on the target // position return 0. if ( x == tx && y == ty ) return dp [ 0 ][ 0 ]; else { // if already calculated then return // that value. Taking absolute difference. if ( dp [ abs ( x - tx )][ abs ( y - ty )] != 0 ) return dp [ abs ( x - tx )][ abs ( y - ty )]; else { // there will be two distinct positions // from the knight towards a target. // if the target is in same row or column // as of knight then there can be four // positions towards the target but in that // two would be the same and the other two // would be the same. int x1 y1 x2 y2 ; // (x1 y1) and (x2 y2) are two positions. // these can be different according to situation. // From position of knight the chess board can be // divided into four blocks i.e.. N-E E-S S-W W-N . if ( x <= tx ) { if ( y <= ty ) { x1 = x + 2 ; y1 = y + 1 ; x2 = x + 1 ; y2 = y + 2 ; } else { x1 = x + 2 ; y1 = y - 1 ; x2 = x + 1 ; y2 = y - 2 ; } } else { if ( y <= ty ) { x1 = x - 2 ; y1 = y + 1 ; x2 = x - 1 ; y2 = y + 2 ; } else { x1 = x - 2 ; y1 = y - 1 ; x2 = x - 1 ; y2 = y - 2 ; } } // ans will be 1 + minimum of steps // required from (x1 y1) and (x2 y2). dp [ abs ( x - tx )][ abs ( y - ty )] = min ( getsteps ( x1 y1 tx ty ) getsteps ( x2 y2 tx ty )) + 1 ; // exchanging the coordinates x with y of both // knight and target will result in same ans. dp [ abs ( y - ty )][ abs ( x - tx )] = dp [ abs ( x - tx )][ abs ( y - ty )]; return dp [ abs ( x - tx )][ abs ( y - ty )]; } } } // Driver Code int main () { int i n x y tx ty ans ; // size of chess board n*n n = 100 ; // (x y) coordinate of the knight. // (tx ty) coordinate of the target position. x = 4 ; y = 5 ; tx = 1 ; ty = 1 ; // (Exception) these are the four corner points // for which the minimum steps is 4. if (( x == 1 && y == 1 && tx == 2 && ty == 2 ) || ( x == 2 && y == 2 && tx == 1 && ty == 1 )) ans = 4 ; else if (( x == 1 && y == n && tx == 2 && ty == n - 1 ) || ( x == 2 && y == n - 1 && tx == 1 && ty == n )) ans = 4 ; else if (( x == n && y == 1 && tx == n - 1 && ty == 2 ) || ( x == n - 1 && y == 2 && tx == n && ty == 1 )) ans = 4 ; else if (( x == n && y == n && tx == n - 1 && ty == n - 1 ) || ( x == n - 1 && y == n - 1 && tx == n && ty == n )) ans = 4 ; else { // dp[a][b] here a b is the difference of // x & tx and y & ty respectively. dp [ 1 ][ 0 ] = 3 ; dp [ 0 ][ 1 ] = 3 ; dp [ 1 ][ 1 ] = 2 ; dp [ 2 ][ 0 ] = 2 ; dp [ 0 ][ 2 ] = 2 ; dp [ 2 ][ 1 ] = 1 ; dp [ 1 ][ 2 ] = 1 ; ans = getsteps ( x y tx ty ); } cout < < ans < < endl ; return 0 ; }
Java //Java code for minimum steps for // a knight to reach target position public class GFG { // initializing the matrix. static int dp [][] = new int [ 8 ][ 8 ] ; static int getsteps ( int x int y int tx int ty ) { // if knight is on the target // position return 0. if ( x == tx && y == ty ) { return dp [ 0 ][ 0 ] ; } else // if already calculated then return // that value. Taking absolute difference. if ( dp [ Math . abs ( x - tx ) ][ Math . abs ( y - ty ) ] != 0 ) { return dp [ Math . abs ( x - tx ) ][ Math . abs ( y - ty ) ] ; } else { // there will be two distinct positions // from the knight towards a target. // if the target is in same row or column // as of knight then there can be four // positions towards the target but in that // two would be the same and the other two // would be the same. int x1 y1 x2 y2 ; // (x1 y1) and (x2 y2) are two positions. // these can be different according to situation. // From position of knight the chess board can be // divided into four blocks i.e.. N-E E-S S-W W-N . if ( x <= tx ) { if ( y <= ty ) { x1 = x + 2 ; y1 = y + 1 ; x2 = x + 1 ; y2 = y + 2 ; } else { x1 = x + 2 ; y1 = y - 1 ; x2 = x + 1 ; y2 = y - 2 ; } } else if ( y <= ty ) { x1 = x - 2 ; y1 = y + 1 ; x2 = x - 1 ; y2 = y + 2 ; } else { x1 = x - 2 ; y1 = y - 1 ; x2 = x - 1 ; y2 = y - 2 ; } // ans will be 1 + minimum of steps // required from (x1 y1) and (x2 y2). dp [ Math . abs ( x - tx ) ][ Math . abs ( y - ty ) ] = Math . min ( getsteps ( x1 y1 tx ty ) getsteps ( x2 y2 tx ty )) + 1 ; // exchanging the coordinates x with y of both // knight and target will result in same ans. dp [ Math . abs ( y - ty ) ][ Math . abs ( x - tx ) ] = dp [ Math . abs ( x - tx ) ][ Math . abs ( y - ty ) ] ; return dp [ Math . abs ( x - tx ) ][ Math . abs ( y - ty ) ] ; } } // Driver Code static public void main ( String [] args ) { int i n x y tx ty ans ; // size of chess board n*n n = 100 ; // (x y) coordinate of the knight. // (tx ty) coordinate of the target position. x = 4 ; y = 5 ; tx = 1 ; ty = 1 ; // (Exception) these are the four corner points // for which the minimum steps is 4. if (( x == 1 && y == 1 && tx == 2 && ty == 2 ) || ( x == 2 && y == 2 && tx == 1 && ty == 1 )) { ans = 4 ; } else if (( x == 1 && y == n && tx == 2 && ty == n - 1 ) || ( x == 2 && y == n - 1 && tx == 1 && ty == n )) { ans = 4 ; } else if (( x == n && y == 1 && tx == n - 1 && ty == 2 ) || ( x == n - 1 && y == 2 && tx == n && ty == 1 )) { ans = 4 ; } else if (( x == n && y == n && tx == n - 1 && ty == n - 1 ) || ( x == n - 1 && y == n - 1 && tx == n && ty == n )) { ans = 4 ; } else { // dp[a][b] here a b is the difference of // x & tx and y & ty respectively. dp [ 1 ][ 0 ] = 3 ; dp [ 0 ][ 1 ] = 3 ; dp [ 1 ][ 1 ] = 2 ; dp [ 2 ][ 0 ] = 2 ; dp [ 0 ][ 2 ] = 2 ; dp [ 2 ][ 1 ] = 1 ; dp [ 1 ][ 2 ] = 1 ; ans = getsteps ( x y tx ty ); } System . out . println ( ans ); } } /*This code is contributed by PrinciRaj1992*/
Python3 # Python3 code for minimum steps for # a knight to reach target position # initializing the matrix. dp = [[ 0 for i in range ( 8 )] for j in range ( 8 )]; def getsteps ( x y tx ty ): # if knight is on the target # position return 0. if ( x == tx and y == ty ): return dp [ 0 ][ 0 ]; # if already calculated then return # that value. Taking absolute difference. elif ( dp [ abs ( x - tx )][ abs ( y - ty )] != 0 ): return dp [ abs ( x - tx )][ abs ( y - ty )]; else : # there will be two distinct positions # from the knight towards a target. # if the target is in same row or column # as of knight then there can be four # positions towards the target but in that # two would be the same and the other two # would be the same. x1 y1 x2 y2 = 0 0 0 0 ; # (x1 y1) and (x2 y2) are two positions. # these can be different according to situation. # From position of knight the chess board can be # divided into four blocks i.e.. N-E E-S S-W W-N . if ( x <= tx ): if ( y <= ty ): x1 = x + 2 ; y1 = y + 1 ; x2 = x + 1 ; y2 = y + 2 ; else : x1 = x + 2 ; y1 = y - 1 ; x2 = x + 1 ; y2 = y - 2 ; elif ( y <= ty ): x1 = x - 2 ; y1 = y + 1 ; x2 = x - 1 ; y2 = y + 2 ; else : x1 = x - 2 ; y1 = y - 1 ; x2 = x - 1 ; y2 = y - 2 ; # ans will be 1 + minimum of steps # required from (x1 y1) and (x2 y2). dp [ abs ( x - tx )][ abs ( y - ty )] = min ( getsteps ( x1 y1 tx ty ) getsteps ( x2 y2 tx ty )) + 1 ; # exchanging the coordinates x with y of both # knight and target will result in same ans. dp [ abs ( y - ty )][ abs ( x - tx )] = dp [ abs ( x - tx )][ abs ( y - ty )]; return dp [ abs ( x - tx )][ abs ( y - ty )]; # Driver Code if __name__ == '__main__' : # size of chess board n*n n = 100 ; # (x y) coordinate of the knight. # (tx ty) coordinate of the target position. x = 4 ; y = 5 ; tx = 1 ; ty = 1 ; # (Exception) these are the four corner points # for which the minimum steps is 4. if (( x == 1 and y == 1 and tx == 2 and ty == 2 ) or ( x == 2 and y == 2 and tx == 1 and ty == 1 )): ans = 4 ; elif (( x == 1 and y == n and tx == 2 and ty == n - 1 ) or ( x == 2 and y == n - 1 and tx == 1 and ty == n )): ans = 4 ; elif (( x == n and y == 1 and tx == n - 1 and ty == 2 ) or ( x == n - 1 and y == 2 and tx == n and ty == 1 )): ans = 4 ; elif (( x == n and y == n and tx == n - 1 and ty == n - 1 ) or ( x == n - 1 and y == n - 1 and tx == n and ty == n )): ans = 4 ; else : # dp[a][b] here a b is the difference of # x & tx and y & ty respectively. dp [ 1 ][ 0 ] = 3 ; dp [ 0 ][ 1 ] = 3 ; dp [ 1 ][ 1 ] = 2 ; dp [ 2 ][ 0 ] = 2 ; dp [ 0 ][ 2 ] = 2 ; dp [ 2 ][ 1 ] = 1 ; dp [ 1 ][ 2 ] = 1 ; ans = getsteps ( x y tx ty ); print ( ans ); # This code is contributed by PrinciRaj1992
C# // C# code for minimum steps for // a knight to reach target position using System ; public class GFG { // initializing the matrix. static int [ ] dp = new int [ 8 8 ]; static int getsteps ( int x int y int tx int ty ) { // if knight is on the target // position return 0. if ( x == tx && y == ty ) { return dp [ 0 0 ]; } else // if already calculated then return // that value. Taking Absolute difference. if ( dp [ Math . Abs ( x - tx ) Math . Abs ( y - ty )] != 0 ) { return dp [ Math . Abs ( x - tx ) Math . Abs ( y - ty )]; } else { // there will be two distinct positions // from the knight towards a target. // if the target is in same row or column // as of knight then there can be four // positions towards the target but in that // two would be the same and the other two // would be the same. int x1 y1 x2 y2 ; // (x1 y1) and (x2 y2) are two positions. // these can be different according to situation. // From position of knight the chess board can be // divided into four blocks i.e.. N-E E-S S-W W-N . if ( x <= tx ) { if ( y <= ty ) { x1 = x + 2 ; y1 = y + 1 ; x2 = x + 1 ; y2 = y + 2 ; } else { x1 = x + 2 ; y1 = y - 1 ; x2 = x + 1 ; y2 = y - 2 ; } } else if ( y <= ty ) { x1 = x - 2 ; y1 = y + 1 ; x2 = x - 1 ; y2 = y + 2 ; } else { x1 = x - 2 ; y1 = y - 1 ; x2 = x - 1 ; y2 = y - 2 ; } // ans will be 1 + minimum of steps // required from (x1 y1) and (x2 y2). dp [ Math . Abs ( x - tx ) Math . Abs ( y - ty )] = Math . Min ( getsteps ( x1 y1 tx ty ) getsteps ( x2 y2 tx ty )) + 1 ; // exchanging the coordinates x with y of both // knight and target will result in same ans. dp [ Math . Abs ( y - ty ) Math . Abs ( x - tx )] = dp [ Math . Abs ( x - tx ) Math . Abs ( y - ty )]; return dp [ Math . Abs ( x - tx ) Math . Abs ( y - ty )]; } } // Driver Code static public void Main () { int i n x y tx ty ans ; // size of chess board n*n n = 100 ; // (x y) coordinate of the knight. // (tx ty) coordinate of the target position. x = 4 ; y = 5 ; tx = 1 ; ty = 1 ; // (Exception) these are the four corner points // for which the minimum steps is 4. if (( x == 1 && y == 1 && tx == 2 && ty == 2 ) || ( x == 2 && y == 2 && tx == 1 && ty == 1 )) { ans = 4 ; } else if (( x == 1 && y == n && tx == 2 && ty == n - 1 ) || ( x == 2 && y == n - 1 && tx == 1 && ty == n )) { ans = 4 ; } else if (( x == n && y == 1 && tx == n - 1 && ty == 2 ) || ( x == n - 1 && y == 2 && tx == n && ty == 1 )) { ans = 4 ; } else if (( x == n && y == n && tx == n - 1 && ty == n - 1 ) || ( x == n - 1 && y == n - 1 && tx == n && ty == n )) { ans = 4 ; } else { // dp[a b] here a b is the difference of // x & tx and y & ty respectively. dp [ 1 0 ] = 3 ; dp [ 0 1 ] = 3 ; dp [ 1 1 ] = 2 ; dp [ 2 0 ] = 2 ; dp [ 0 2 ] = 2 ; dp [ 2 1 ] = 1 ; dp [ 1 2 ] = 1 ; ans = getsteps ( x y tx ty ); } Console . WriteLine ( ans ); } } /*This code is contributed by PrinciRaj1992*/
JavaScript < script > // JavaScript code for minimum steps for // a knight to reach target position // initializing the matrix. let dp = new Array ( 8 ) for ( let i = 0 ; i < 8 ; i ++ ){ dp [ i ] = new Array ( 8 ). fill ( 0 ) } function getsteps ( x y tx ty ) { // if knight is on the target // position return 0. if ( x == tx && y == ty ) return dp [ 0 ][ 0 ]; else { // if already calculated then return // that value. Taking absolute difference. if ( dp [( Math . abs ( x - tx ))][( Math . abs ( y - ty ))] != 0 ) return dp [( Math . abs ( x - tx ))][( Math . abs ( y - ty ))]; else { // there will be two distinct positions // from the knight towards a target. // if the target is in same row or column // as of knight then there can be four // positions towards the target but in that // two would be the same and the other two // would be the same. let x1 y1 x2 y2 ; // (x1 y1) and (x2 y2) are two positions. // these can be different according to situation. // From position of knight the chess board can be // divided into four blocks i.e.. N-E E-S S-W W-N . if ( x <= tx ) { if ( y <= ty ) { x1 = x + 2 ; y1 = y + 1 ; x2 = x + 1 ; y2 = y + 2 ; } else { x1 = x + 2 ; y1 = y - 1 ; x2 = x + 1 ; y2 = y - 2 ; } } else { if ( y <= ty ) { x1 = x - 2 ; y1 = y + 1 ; x2 = x - 1 ; y2 = y + 2 ; } else { x1 = x - 2 ; y1 = y - 1 ; x2 = x - 1 ; y2 = y - 2 ; } } // ans will be 1 + minimum of steps // required from (x1 y1) and (x2 y2). dp [( Math . abs ( x - tx ))][( Math . abs ( y - ty ))] = Math . min ( getsteps ( x1 y1 tx ty ) getsteps ( x2 y2 tx ty )) + 1 ; // exchanging the coordinates x with y of both // knight and target will result in same ans. dp [( Math . abs ( y - ty ))][( Math . abs ( x - tx ))] = dp [( Math . abs ( x - tx ))][( Math . abs ( y - ty ))]; return dp [( Math . abs ( x - tx ))][( Math . abs ( y - ty ))]; } } } // Driver Code let i n x y tx ty ans ; // size of chess board n*n n = 100 ; // (x y) coordinate of the knight. // (tx ty) coordinate of the target position. x = 4 ; y = 5 ; tx = 1 ; ty = 1 ; // (Exception) these are the four corner points // for which the minimum steps is 4. if (( x == 1 && y == 1 && tx == 2 && ty == 2 ) || ( x == 2 && y == 2 && tx == 1 && ty == 1 )) ans = 4 ; else if (( x == 1 && y == n && tx == 2 && ty == n - 1 ) || ( x == 2 && y == n - 1 && tx == 1 && ty == n )) ans = 4 ; else if (( x == n && y == 1 && tx == n - 1 && ty == 2 ) || ( x == n - 1 && y == 2 && tx == n && ty == 1 )) ans = 4 ; else if (( x == n && y == n && tx == n - 1 && ty == n - 1 ) || ( x == n - 1 && y == n - 1 && tx == n && ty == n )) ans = 4 ; else { // dp[a][b] here a b is the difference of // x & tx and y & ty respectively. dp [ 1 ][ 0 ] = 3 ; dp [ 0 ][ 1 ] = 3 ; dp [ 1 ][ 1 ] = 2 ; dp [ 2 ][ 0 ] = 2 ; dp [ 0 ][ 2 ] = 2 ; dp [ 2 ][ 1 ] = 1 ; dp [ 1 ][ 2 ] = 1 ; ans = getsteps ( x y tx ty ); } document . write ( ans ' ' ); // This code is contributed by shinjanpatra. < /script>
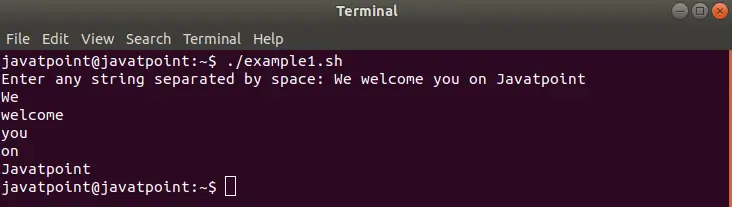
Sortida:
3
Complexitat temporal: O(N * M) on N és el nombre total de files i M és el nombre total de columnes
Espai auxiliar: O (N * M)