المماس بين مضلعين محدبين
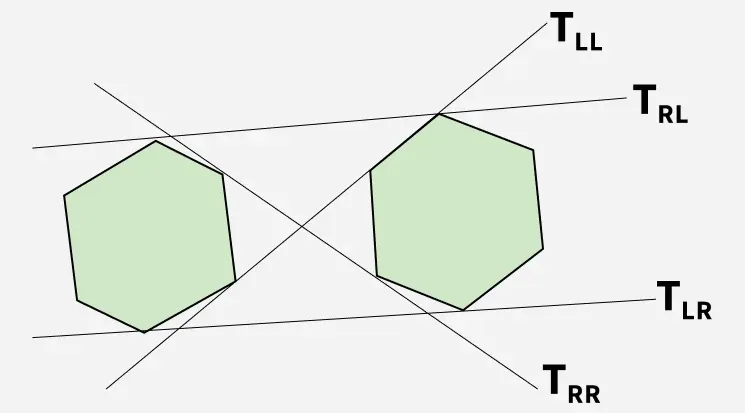
بالنظر إلى مضلعين محدبين، فإننا نهدف إلى تحديد المماس السفلي والعلوي الذي يربط بينهما.
كما هو مبين في الشكل أدناه ت رل و ت إل آر تمثل الظلال العلوية والسفلية على التوالي.

أمثلة:
مدخل: المضلع الأول : [[2 2] [3 3] [5 2] [4 0] [3 1]]
المضلع الثاني : [[-1 0] [0 1] [1 0] [0 -2]].
الإخراج: الظل العلوي - ربط الخط (01) و (33)
الظل السفلي - ربط الخط (0-2) و (40)
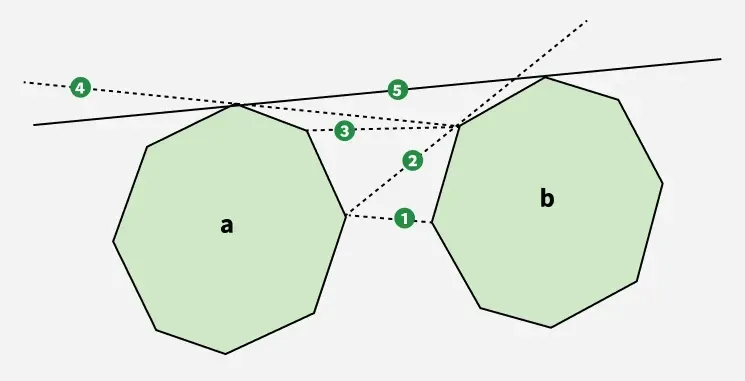
توضيح: تُظهر الصورة بوضوح البنية والمماسات التي تربط المضلعين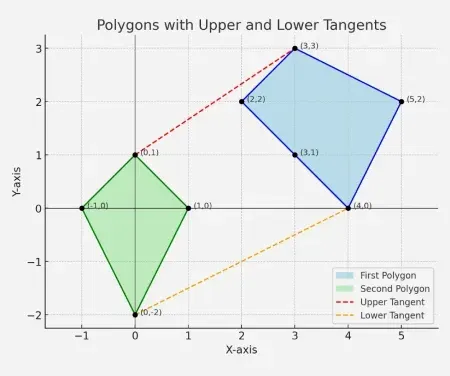
يقترب:
للعثور على المماس العلوي نبدأ باختيار نقطتين: النقطة الموجودة في أقصى يمين المضلع أ والنقطة الموجودة في أقصى يسار المضلع ب . يتم تسمية الخط الذي يصل بين هاتين النقطتين باسم السطر 1 . لأن هذا الخط يمر عبر المضلع ب (أي أنها ليست فوقها تمامًا) ننتقل إلى النقطة التالية في اتجاه عكس اتجاه عقارب الساعة ب تشكيل خط 2 . هذا الخط موجود الآن فوق المضلع ب وهو أمر جيد. ومع ذلك فإنه يعبر المضلع أ لذلك ننتقل إلى النقطة التالية أ في اتجاه عقارب الساعة خلق السطر 3 . السطر 3 لا يزال يعبر المضلع أ مما دفع إلى التحرك آخر ل السطر 4 . السطر 4 ولكن يعبر المضلع ب لذلك ننتقل إلى السطر 5 . أخيراً السطر 5 لا يتقاطع مع أي من المضلعين مما يجعله الظل العلوي الصحيح للمضلعات المحددة.
للعثور على المماس السفلي، نحتاج إلى التحرك بشكل عكسي عبر المضلعات، أي إذا كان الخط يعبر المضلع b، فإننا نتحرك إلى اتجاه عقارب الساعة بعد ذلك وإلى عكس اتجاه عقارب الساعة إذا كان الخط يعبر المضلع a.
خوارزمية الظل العلوي:
ل ← الخط الذي يصل بين النقطة الواقعة في أقصى اليمين من النقطة a وفي أقصى اليسار من النقطة b. بينما (L يعبر أيًا من المضلعات) { بينما (L يعبر b) L ← L' : النقطة الموجودة على b تتحرك لأعلى. بينما (L يعبر أ) L ← L' : النقطة التي تتحرك لأعلى. }
خوارزمية المماس السفلي:
ل ← الخط الذي يصل بين النقطة الواقعة في أقصى اليمين من النقطة a وفي أقصى اليسار من النقطة b. بينما (L يعبر أيًا من المضلعات) {بينما (L يعبر b) L ← L' : النقطة الموجودة على b تتحرك لأسفل. بينما (L يعبر أ) L ← L' : النقطة التي تتحرك لأسفل. }
لاحظ أن الكود أعلاه يحسب الظل العلوي فقط. يمكن استخدام طريقة مماثلة للعثور على المماس السفلي أيضًا.
CPP #include using namespace std ; // Determines the quadrant of a point relative to origin int quad ( vector < int > p ) { if ( p [ 0 ] >= 0 && p [ 1 ] >= 0 ) return 1 ; if ( p [ 0 ] <= 0 && p [ 1 ] >= 0 ) return 2 ; if ( p [ 0 ] <= 0 && p [ 1 ] <= 0 ) return 3 ; return 4 ; } // Returns the orientation of ordered triplet (a b c) // 0 -> Collinear 1 -> Clockwise -1 -> Counterclockwise int orientation ( vector < int > a vector < int > b vector < int > c ) { int res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]); if ( res == 0 ) return 0 ; if ( res > 0 ) return 1 ; return -1 ; } // Compare function to sort points counter-clockwise around center bool compare ( vector < int > p1 vector < int > q1 vector < int > mid ) { vector < int > p = { p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ]}; vector < int > q = { q1 [ 0 ] - mid [ 0 ] q1 [ 1 ] - mid [ 1 ]}; int one = quad ( p ); int two = quad ( q ); if ( one != two ) return ( one < two ); return ( p [ 1 ] * q [ 0 ] < q [ 1 ] * p [ 0 ]); } // Sorts the polygon points counter-clockwise vector < vector < int >> sortPoints ( vector < vector < int >> polygon ) { vector < int > mid = { 0 0 }; int n = polygon . size (); // Calculate center (centroid) of the polygon for ( int i = 0 ; i < n ; i ++ ) { mid [ 0 ] += polygon [ i ][ 0 ]; mid [ 1 ] += polygon [ i ][ 1 ]; polygon [ i ][ 0 ] *= n ; polygon [ i ][ 1 ] *= n ; } // Sort points based on their angle from the center sort ( polygon . begin () polygon . end () [ mid ]( vector < int > p1 vector < int > p2 ) { return compare ( p1 p2 mid ); }); // Divide back to original coordinates for ( int i = 0 ; i < n ; i ++ ) { polygon [ i ][ 0 ] /= n ; polygon [ i ][ 1 ] /= n ; } return polygon ; } // Finds the upper tangent between two convex polygons a and b // Returns two points forming the upper tangent vector < vector < int >> findUpperTangent ( vector < vector < int >> a vector < vector < int >> b ) { int n1 = a . size () n2 = b . size (); // Find the rightmost point of polygon a and leftmost point of polygon b int maxa = INT_MIN ; for ( auto & p : a ) maxa = max ( maxa p [ 0 ]); int minb = INT_MAX ; for ( auto & p : b ) minb = min ( minb p [ 0 ]); // Sort both polygons counter-clockwise a = sortPoints ( a ); b = sortPoints ( b ); // Ensure polygon a is to the left of polygon b if ( minb < maxa ) swap ( a b ); n1 = a . size (); n2 = b . size (); // Find the rightmost point in a int ia = 0 ib = 0 ; for ( int i = 1 ; i < n1 ; i ++ ) if ( a [ i ][ 0 ] > a [ ia ][ 0 ]) ia = i ; // Find the leftmost point in b for ( int i = 1 ; i < n2 ; i ++ ) if ( b [ i ][ 0 ] < b [ ib ][ 0 ]) ib = i ; // Initialize starting points int inda = ia indb = ib ; bool done = false ; // Find upper tangent using orientation checks while ( ! done ) { done = true ; // Move to next point in a if necessary while ( orientation ( b [ indb ] a [ inda ] a [( inda + 1 ) % n1 ]) > 0 ) inda = ( inda + 1 ) % n1 ; // Move to previous point in b if necessary while ( orientation ( a [ inda ] b [ indb ] b [( n2 + indb - 1 ) % n2 ]) < 0 ) { indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } // Return the points forming the upper tangent return { a [ inda ] b [ indb ]}; } // Main driver code int main () { vector < vector < int >> a = {{ 2 2 } { 3 1 } { 3 3 } { 5 2 } { 4 0 }}; vector < vector < int >> b = {{ 0 1 } { 1 0 } { 0 -2 } { -1 0 }}; vector < vector < int >> tangent = findUpperTangent ( a b ); for ( auto it : tangent ){ cout < < it [ 0 ] < < ' ' < < it [ 1 ] < < ' n ' ; } return 0 ; }
Java import java.util.* ; class GfG { // Determines the quadrant of a point static int quad ( int [] p ) { if ( p [ 0 ] >= 0 && p [ 1 ] >= 0 ) return 1 ; if ( p [ 0 ] <= 0 && p [ 1 ] >= 0 ) return 2 ; if ( p [ 0 ] <= 0 && p [ 1 ] <= 0 ) return 3 ; return 4 ; } // Checks whether the line is crossing the polygon static int orientation ( int [] a int [] b int [] c ) { int res = ( b [ 1 ] - a [ 1 ] ) * ( c [ 0 ] - b [ 0 ] ) - ( c [ 1 ] - b [ 1 ] ) * ( b [ 0 ] - a [ 0 ] ); if ( res == 0 ) return 0 ; if ( res > 0 ) return 1 ; return - 1 ; } // Compare function for sorting static class PointComparator implements Comparator < int []> { int [] mid ; public PointComparator ( int [] mid ) { this . mid = mid ; } public int compare ( int [] p1 int [] p2 ) { int [] p = { p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ] }; int [] q = { p2 [ 0 ] - mid [ 0 ] p2 [ 1 ] - mid [ 1 ] }; int one = quad ( p ); int two = quad ( q ); if ( one != two ) return one - two ; return p [ 1 ] * q [ 0 ] - q [ 1 ] * p [ 0 ] ; } } // Finds upper tangent of two polygons 'a' and 'b' // represented as 2D arrays and stores the result static int [][] findUpperTangent ( int [][] a int [][] b ) { // n1 -> number of points in polygon a // n2 -> number of points in polygon b int n1 = a . length n2 = b . length ; int [] mid = { 0 0 }; int maxa = Integer . MIN_VALUE ; // Calculate centroid for polygon a and adjust points for scaling for ( int i = 0 ; i < n1 ; i ++ ) { maxa = Math . max ( maxa a [ i ][ 0 ] ); mid [ 0 ] += a [ i ][ 0 ] ; mid [ 1 ] += a [ i ][ 1 ] ; a [ i ][ 0 ] *= n1 ; a [ i ][ 1 ] *= n1 ; } // Sorting the points in counter-clockwise order for polygon a Arrays . sort ( a new PointComparator ( mid )); for ( int i = 0 ; i < n1 ; i ++ ) { a [ i ][ 0 ] /= n1 ; a [ i ][ 1 ] /= n1 ; } mid [ 0 ] = 0 ; mid [ 1 ] = 0 ; int minb = Integer . MAX_VALUE ; // Calculate centroid for polygon b and adjust points for scaling for ( int i = 0 ; i < n2 ; i ++ ) { mid [ 0 ] += b [ i ][ 0 ] ; mid [ 1 ] += b [ i ][ 1 ] ; minb = Math . min ( minb b [ i ][ 0 ] ); b [ i ][ 0 ] *= n2 ; b [ i ][ 1 ] *= n2 ; } // Sorting the points in counter-clockwise order for polygon b Arrays . sort ( b new PointComparator ( mid )); for ( int i = 0 ; i < n2 ; i ++ ) { b [ i ][ 0 ] /= n2 ; b [ i ][ 1 ] /= n2 ; } // If a is to the right of b swap a and b if ( minb < maxa ) { int [][] temp = a ; a = b ; b = temp ; n1 = a . length ; n2 = b . length ; } // ia -> rightmost point of a int ia = 0 ib = 0 ; for ( int i = 1 ; i < n1 ; i ++ ) { if ( a [ i ][ 0 ] > a [ ia ][ 0 ] ) ia = i ; } // ib -> leftmost point of b for ( int i = 1 ; i < n2 ; i ++ ) { if ( b [ i ][ 0 ] < b [ ib ][ 0 ] ) ib = i ; } // Finding the upper tangent int inda = ia indb = ib ; boolean done = false ; while ( ! done ) { done = true ; while ( orientation ( b [ indb ] a [ inda ] a [ ( inda + 1 ) % n1 ] ) > 0 ) inda = ( inda + 1 ) % n1 ; while ( orientation ( a [ inda ] b [ indb ] b [ ( n2 + indb - 1 ) % n2 ] ) < 0 ) { indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } // Returning the upper tangent as a 2D array return new int [][] { { a [ inda ][ 0 ] a [ inda ][ 1 ] } { b [ indb ][ 0 ] b [ indb ][ 1 ] } }; } // Driver code public static void main ( String [] args ) { int [][] a = {{ 2 2 }{ 3 1 }{ 3 3 }{ 5 2 }{ 4 0 }}; int [][] b = {{ 0 1 }{ 1 0 }{ 0 - 2 }{ - 1 0 }}; // Get the upper tangent as a 2D array int [][] upperTangent = findUpperTangent ( a b ); // Store or use the result System . out . println ( upperTangent [ 0 ][ 0 ] + ' ' + upperTangent [ 0 ][ 1 ] ); System . out . println ( upperTangent [ 1 ][ 0 ] + ' ' + upperTangent [ 1 ][ 1 ] ); } }
Python from functools import cmp_to_key def quad ( p ): if p [ 0 ] >= 0 and p [ 1 ] >= 0 : return 1 if p [ 0 ] <= 0 and p [ 1 ] >= 0 : return 2 if p [ 0 ] <= 0 and p [ 1 ] <= 0 : return 3 return 4 def orientation ( a b c ): res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]) if res == 0 : return 0 if res > 0 : return 1 return - 1 def compare ( mid ): def cmp ( p1 q1 ): p = [ p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ]] q = [ q1 [ 0 ] - mid [ 0 ] q1 [ 1 ] - mid [ 1 ]] one = quad ( p ) two = quad ( q ) if one != two : return one - two if p [ 1 ] * q [ 0 ] < q [ 1 ] * p [ 0 ]: return - 1 return 1 return cmp def findUpperTangent ( a b ): n1 n2 = len ( a ) len ( b ) mid_a = [ 0 0 ] maxa = float ( '-inf' ) for i in range ( n1 ): maxa = max ( maxa a [ i ][ 0 ]) mid_a [ 0 ] += a [ i ][ 0 ] mid_a [ 1 ] += a [ i ][ 1 ] a = sorted ( a key = cmp_to_key ( compare ( mid_a ))) mid_b = [ 0 0 ] minb = float ( 'inf' ) for i in range ( n2 ): minb = min ( minb b [ i ][ 0 ]) mid_b [ 0 ] += b [ i ][ 0 ] mid_b [ 1 ] += b [ i ][ 1 ] b = sorted ( b key = cmp_to_key ( compare ( mid_b ))) if minb < maxa : a b = b a n1 n2 = n2 n1 ia = 0 for i in range ( 1 n1 ): if a [ i ][ 0 ] > a [ ia ][ 0 ]: ia = i ib = 0 for i in range ( 1 n2 ): if b [ i ][ 0 ] < b [ ib ][ 0 ]: ib = i inda indb = ia ib done = False while not done : done = True while orientation ( b [ indb ] a [ inda ] a [( inda + 1 ) % n1 ]) > 0 : inda = ( inda + 1 ) % n1 while orientation ( a [ inda ] b [ indb ] b [( n2 + indb - 1 ) % n2 ]) < 0 : indb = ( n2 + indb - 1 ) % n2 done = False # return integer coordinates return [[ int ( a [ inda ][ 0 ]) int ( a [ inda ][ 1 ])] [ int ( b [ indb ][ 0 ]) int ( b [ indb ][ 1 ])]] # Driver Code if __name__ == '__main__' : a = [ [ 2 2 ] [ 3 1 ] [ 3 3 ] [ 5 2 ] [ 4 0 ] ] b = [ [ 0 1 ] [ 1 0 ] [ 0 - 2 ] [ - 1 0 ] ] upperTangent = findUpperTangent ( a b ) for point in upperTangent : print ( f ' { point [ 0 ] } { point [ 1 ] } ' )
C# using System ; public class UpperTangentFinder { static int Quad ( int x int y ) { if ( x >= 0 && y >= 0 ) return 1 ; if ( x <= 0 && y >= 0 ) return 2 ; if ( x <= 0 && y <= 0 ) return 3 ; return 4 ; } static int Orientation ( int [] a int [] b int [] c ) { int res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]); if ( res == 0 ) return 0 ; return res > 0 ? 1 : - 1 ; } static bool Compare ( int [] p1 int [] p2 int [] mid ) { int [] p = { p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ] }; int [] q = { p2 [ 0 ] - mid [ 0 ] p2 [ 1 ] - mid [ 1 ] }; int quadP = Quad ( p [ 0 ] p [ 1 ]); int quadQ = Quad ( q [ 0 ] q [ 1 ]); if ( quadP != quadQ ) return quadP < quadQ ; return ( p [ 1 ] * q [ 0 ]) < ( q [ 1 ] * p [ 0 ]); } static int [] SortPoints ( int [] polygon ) { int n = polygon . GetLength ( 0 ); int [] mid = { 0 0 }; for ( int i = 0 ; i < n ; i ++ ) { mid [ 0 ] += polygon [ i 0 ]; mid [ 1 ] += polygon [ i 1 ]; polygon [ i 0 ] *= n ; polygon [ i 1 ] *= n ; } for ( int i = 0 ; i < n - 1 ; i ++ ) { for ( int j = i + 1 ; j < n ; j ++ ) { int [] p1 = { polygon [ i 0 ] polygon [ i 1 ] }; int [] p2 = { polygon [ j 0 ] polygon [ j 1 ] }; if ( ! Compare ( p1 p2 mid )) { int tempX = polygon [ i 0 ] tempY = polygon [ i 1 ]; polygon [ i 0 ] = polygon [ j 0 ]; polygon [ i 1 ] = polygon [ j 1 ]; polygon [ j 0 ] = tempX ; polygon [ j 1 ] = tempY ; } } } for ( int i = 0 ; i < n ; i ++ ) { polygon [ i 0 ] /= n ; polygon [ i 1 ] /= n ; } return polygon ; } static int [] FindUpperTangent ( int [] a int [] b ) { int n1 = a . GetLength ( 0 ); int n2 = b . GetLength ( 0 ); int maxa = int . MinValue ; for ( int i = 0 ; i < n1 ; i ++ ) maxa = Math . Max ( maxa a [ i 0 ]); int minb = int . MaxValue ; for ( int i = 0 ; i < n2 ; i ++ ) minb = Math . Min ( minb b [ i 0 ]); a = SortPoints ( a ); b = SortPoints ( b ); if ( minb < maxa ) { int [] temp = a ; a = b ; b = temp ; n1 = a . GetLength ( 0 ); n2 = b . GetLength ( 0 ); } int ia = 0 ib = 0 ; for ( int i = 1 ; i < n1 ; i ++ ) if ( a [ i 0 ] > a [ ia 0 ]) ia = i ; for ( int i = 1 ; i < n2 ; i ++ ) if ( b [ i 0 ] < b [ ib 0 ]) ib = i ; int inda = ia indb = ib ; bool done = false ; while ( ! done ) { done = true ; while ( Orientation ( new int [] { b [ indb 0 ] b [ indb 1 ] } new int [] { a [ inda 0 ] a [ inda 1 ] } new int [] { a [( inda + 1 ) % n1 0 ] a [( inda + 1 ) % n1 1 ] }) > 0 ){ inda = ( inda + 1 ) % n1 ; } while ( Orientation ( new int [] { a [ inda 0 ] a [ inda 1 ] } new int [] { b [ indb 0 ] b [ indb 1 ] } new int [] { b [( n2 + indb - 1 ) % n2 0 ] b [( n2 + indb - 1 ) % n2 1 ] }) < 0 ){ indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } int [] result = new int [ 2 2 ]; result [ 0 0 ] = a [ inda 0 ]; result [ 0 1 ] = a [ inda 1 ]; result [ 1 0 ] = b [ indb 0 ]; result [ 1 1 ] = b [ indb 1 ]; return result ; } public static void Main ( string [] args ) { int [] a = new int [] { { 2 2 } { 3 1 } { 3 3 } { 5 2 } { 4 0 } }; int [] b = new int [] { { 0 1 } { 1 0 } { 0 - 2 } { - 1 0 } }; int [] tangent = FindUpperTangent ( a b ); for ( int i = 0 ; i < 2 ; i ++ ) { Console . WriteLine ( tangent [ i 0 ] + ' ' + tangent [ i 1 ]); } } }
JavaScript // Determine the quadrant of a point function quad ( p ) { if ( p [ 0 ] >= 0 && p [ 1 ] >= 0 ) return 1 ; if ( p [ 0 ] <= 0 && p [ 1 ] >= 0 ) return 2 ; if ( p [ 0 ] <= 0 && p [ 1 ] <= 0 ) return 3 ; return 4 ; } // Find orientation of triplet (a b c) function orientation ( a b c ) { let res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]); if ( res === 0 ) return 0 ; return res > 0 ? 1 : - 1 ; } // Compare two points based on mid function compare ( p1 p2 mid ) { let p = [ p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ]]; let q = [ p2 [ 0 ] - mid [ 0 ] p2 [ 1 ] - mid [ 1 ]]; let quadP = quad ( p ); let quadQ = quad ( q ); if ( quadP !== quadQ ) return quadP - quadQ ; return ( p [ 1 ] * q [ 0 ]) - ( q [ 1 ] * p [ 0 ]); } // Sort polygon points counter-clockwise function sortPoints ( polygon ) { let n = polygon . length ; let mid = [ 0 0 ]; for ( let i = 0 ; i < n ; i ++ ) { mid [ 0 ] += polygon [ i ][ 0 ]; mid [ 1 ] += polygon [ i ][ 1 ]; polygon [ i ][ 0 ] *= n ; polygon [ i ][ 1 ] *= n ; } polygon . sort (( p1 p2 ) => compare ( p1 p2 mid )); for ( let i = 0 ; i < n ; i ++ ) { polygon [ i ][ 0 ] = Math . floor ( polygon [ i ][ 0 ] / n ); polygon [ i ][ 1 ] = Math . floor ( polygon [ i ][ 1 ] / n ); } return polygon ; } // Find upper tangent between two convex polygons function findUpperTangent ( a b ) { let n1 = a . length ; let n2 = b . length ; let maxa = - Infinity ; for ( let i = 0 ; i < n1 ; i ++ ) maxa = Math . max ( maxa a [ i ][ 0 ]); let minb = Infinity ; for ( let i = 0 ; i < n2 ; i ++ ) minb = Math . min ( minb b [ i ][ 0 ]); a = sortPoints ( a ); b = sortPoints ( b ); if ( minb < maxa ) { let temp = a ; a = b ; b = temp ; n1 = a . length ; n2 = b . length ; } let ia = 0 ib = 0 ; for ( let i = 1 ; i < n1 ; i ++ ) if ( a [ i ][ 0 ] > a [ ia ][ 0 ]) ia = i ; for ( let i = 1 ; i < n2 ; i ++ ) if ( b [ i ][ 0 ] < b [ ib ][ 0 ]) ib = i ; let inda = ia indb = ib ; let done = false ; while ( ! done ) { done = true ; while ( orientation ( b [ indb ] a [ inda ] a [( inda + 1 ) % n1 ]) > 0 ) inda = ( inda + 1 ) % n1 ; while ( orientation ( a [ inda ] b [ indb ] b [( n2 + indb - 1 ) % n2 ]) < 0 ) { indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } return [ a [ inda ] b [ indb ]]; } // Driver code let a = [[ 2 2 ][ 3 1 ][ 3 3 ][ 5 2 ][ 4 0 ]]; let b = [[ 0 1 ][ 1 0 ][ 0 - 2 ][ - 1 0 ]]; let tangent = findUpperTangent ( a b ); for ( let point of tangent ) { console . log ( point [ 0 ] + ' ' + point [ 1 ]); }
الإخراج
upper tangent (01) (33)
تعقيد الوقت: O(سجل n1 (n1) + سجل n2(n2))
المساحة المساعدة: يا(1)