خوارزمية الحذف العكسي للحد الأدنى من الشجرة الممتدة

جربه على ممارسة GfG خوارزمية الحذف العكسي للحد الأدنى من الشجرة الممتدة

#practiceLinkDiv { العرض: لا شيء! مهم؛ }

ترتبط خوارزمية الحذف العكسي ارتباطًا وثيقًا بـ خوارزمية كروسكال . ما نقوم به في خوارزمية كروسكال هو: فرز الحواف عن طريق زيادة ترتيب أوزانها. بعد الفرز نقوم باختيار الحواف واحدة تلو الأخرى بترتيب متزايد. نقوم بتضمين الحافة المنتقاة الحالية إذا لم يشكل تضمين هذا في الشجرة الممتدة أي دورة حتى تكون هناك حواف V-1 في الشجرة الممتدة حيث V = عدد القمم.

في خوارزمية الحذف العكسي، نقوم بفرز جميع الحواف متناقص ترتيب أوزانهم. بعد الفرز نقوم باختيار الحواف واحدة تلو الأخرى بترتيب تنازلي. نحن قم بتضمين الحافة المختارة الحالية إذا كان استبعاد الحافة الحالية يؤدي إلى انقطاع الاتصال في الرسم البياني الحالي . الفكرة الرئيسية هي حذف الحافة إذا كان حذفها لا يؤدي إلى انقطاع الرسم البياني.

الخوارزمية :

قم بفرز جميع حواف الرسم البياني بترتيب غير تصاعدي لأوزان الحواف.

قم بتهيئة MST كرسم بياني أصلي وقم بإزالة الحواف الإضافية باستخدام الخطوة 3.

اختر حافة الوزن الأعلى من الحواف المتبقية و تحقق مما إذا كان حذف الحافة يؤدي إلى قطع اتصال الرسم البياني أم لا .
إذا تم قطع الاتصال فإننا لا نحذف الحافة.
وإلا فإننا نحذف الحافة ونستمر.

توضيح:

دعونا نفهم من خلال المثال التالي:

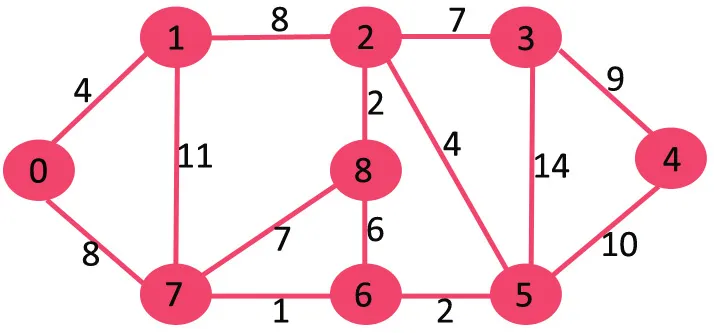
عكس الحذف2

إذا قمنا بحذف حافة الوزن الأعلى للوزن 14 رسمًا بيانيًا فلن يتم قطع الاتصال لذلك نقوم بإزالته.

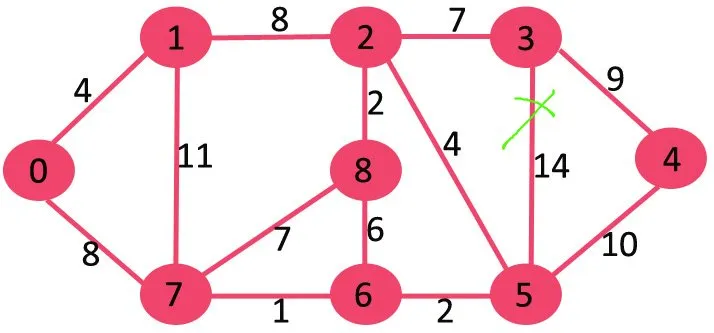
الحذف العكسي3

بعد ذلك نحذف 11 لأن حذفه لا يؤدي إلى قطع اتصال الرسم البياني.

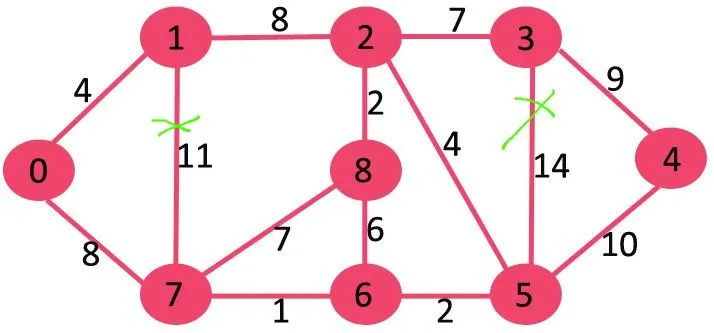
الحذف العكسي4

بعد ذلك نحذف 10 لأن حذفها لا يؤدي إلى قطع اتصال الرسم البياني.

الحذف العكسي5

التالي هو 9. لا يمكننا حذف 9 لأن حذفها يؤدي إلى قطع الاتصال.

نواصل بهذه الطريقة وتبقى الحواف التالية في MST النهائي.

 Edges in MST   
 (3 4)    
 (0 7)    
 (2 3)    
 (2 5)    
 (0 1)    
 (5 6)    
 (2 8)    
 (6 7)    
     ملحوظة :    في حالة الحواف ذات الوزن نفسه يمكننا اختيار أي حافة لها نفس الوزن.  
الممارسة الموصى بها خوارزمية الحذف العكسي للحد الأدنى من الشجرة الممتدة    جربه!       تطبيق:    
 C++      // C++ program to find Minimum Spanning Tree   // of a graph using Reverse Delete Algorithm   #include       using     namespace     std  ;   // Creating shortcut for an integer pair   typedef     pair   <  int       int  >     iPair  ;   // Graph class represents a directed graph   // using adjacency list representation   class     Graph   {      int     V  ;     // No. of vertices      list   <  int  >     *  adj  ;      vector   <     pair   <  int       iPair  >     >     edges  ;      void     DFS  (  int     v       bool     visited  []);   public  :      Graph  (  int     V  );     // Constructor      // function to add an edge to graph      void     addEdge  (  int     u       int     v       int     w  );      // Returns true if graph is connected      bool     isConnected  ();      void     reverseDeleteMST  ();   };   Graph  ::  Graph  (  int     V  )   {      this  ->  V     =     V  ;      adj     =     new     list   <  int  >  [  V  ];   }   void     Graph  ::  addEdge  (  int     u       int     v       int     w  )   {      adj  [  u  ].  push_back  (  v  );     // Add w to v’s list.      adj  [  v  ].  push_back  (  u  );     // Add w to v’s list.      edges  .  push_back  ({  w       {  u       v  }});   }   void     Graph  ::  DFS  (  int     v       bool     visited  [])   {      // Mark the current node as visited and print it      visited  [  v  ]     =     true  ;      // Recur for all the vertices adjacent to      // this vertex      list   <  int  >::  iterator     i  ;      for     (  i     =     adj  [  v  ].  begin  ();     i     !=     adj  [  v  ].  end  ();     ++  i  )      if     (  !  visited  [  *  i  ])      DFS  (  *  i       visited  );   }   // Returns true if given graph is connected else false   bool     Graph  ::  isConnected  ()   {      bool     visited  [  V  ];      memset  (  visited       false       sizeof  (  visited  ));      // Find all reachable vertices from first vertex      DFS  (  0       visited  );      // If set of reachable vertices includes all      // return true.      for     (  int     i  =  1  ;     i   <  V  ;     i  ++  )      if     (  visited  [  i  ]     ==     false  )      return     false  ;      return     true  ;   }   // This function assumes that edge (u v)   // exists in graph or not   void     Graph  ::  reverseDeleteMST  ()   {      // Sort edges in increasing order on basis of cost      sort  (  edges  .  begin  ()     edges  .  end  ());      int     mst_wt     =     0  ;     // Initialize weight of MST      cout      < <     'Edges in MST  n  '  ;      // Iterate through all sorted edges in      // decreasing order of weights      for     (  int     i  =  edges  .  size  ()  -1  ;     i  >=  0  ;     i  --  )      {      int     u     =     edges  [  i  ].  second  .  first  ;      int     v     =     edges  [  i  ].  second  .  second  ;      // Remove edge from undirected graph      adj  [  u  ].  remove  (  v  );      adj  [  v  ].  remove  (  u  );      // Adding the edge back if removing it      // causes disconnection. In this case this       // edge becomes part of MST.      if     (  isConnected  ()     ==     false  )      {      adj  [  u  ].  push_back  (  v  );      adj  [  v  ].  push_back  (  u  );      // This edge is part of MST      cout      < <     '('      < <     u      < <     ' '      < <     v      < <     ')   n  '  ;      mst_wt     +=     edges  [  i  ].  first  ;      }      }      cout      < <     'Total weight of MST is '      < <     mst_wt  ;   }   // Driver code   int     main  ()   {      // create the graph given in above figure      int     V     =     9  ;      Graph     g  (  V  );      // making above shown graph      g  .  addEdge  (  0       1       4  );      g  .  addEdge  (  0       7       8  );      g  .  addEdge  (  1       2       8  );      g  .  addEdge  (  1       7       11  );      g  .  addEdge  (  2       3       7  );      g  .  addEdge  (  2       8       2  );      g  .  addEdge  (  2       5       4  );      g  .  addEdge  (  3       4       9  );      g  .  addEdge  (  3       5       14  );      g  .  addEdge  (  4       5       10  );      g  .  addEdge  (  5       6       2  );      g  .  addEdge  (  6       7       1  );      g  .  addEdge  (  6       8       6  );      g  .  addEdge  (  7       8       7  );      g  .  reverseDeleteMST  ();      return     0  ;   }   
  Java      // Java program to find Minimum Spanning Tree   // of a graph using Reverse Delete Algorithm   import     java.util.*  ;   // class to represent an edge   class   Edge     implements     Comparable   <  Edge  >     {      int     u       v       w  ;      Edge  (  int     u       int     v       int     w  )      {      this  .  u     =     u  ;      this  .  w     =     w  ;      this  .  v     =     v  ;      }      public     int     compareTo  (  Edge     other  )      {      return     (  this  .  w     -     other  .  w  );      }   }   // Class to represent a graph using adjacency list   // representation   public     class   GFG     {      private     int     V  ;     // No. of vertices      private     List   <  Integer  >[]     adj  ;      private     List   <  Edge  >     edges  ;      @SuppressWarnings  ({     'unchecked'       'deprecated'     })      public     GFG  (  int     v  )     // Constructor      {      V     =     v  ;      adj     =     new     ArrayList  [  v  ]  ;      for     (  int     i     =     0  ;     i      <     v  ;     i  ++  )      adj  [  i  ]     =     new     ArrayList   <  Integer  >  ();      edges     =     new     ArrayList   <  Edge  >  ();      }      // function to Add an edge      public     void     AddEdge  (  int     u       int     v       int     w  )      {      adj  [  u  ]  .  add  (  v  );     // Add w to v’s list.      adj  [  v  ]  .  add  (  u  );     // Add w to v’s list.      edges  .  add  (  new     Edge  (  u       v       w  ));      }      // function to perform dfs      private     void     DFS  (  int     v       boolean  []     visited  )      {      // Mark the current node as visited and print it      visited  [  v  ]     =     true  ;      // Recur for all the vertices adjacent to      // this vertex      for     (  int     i     :     adj  [  v  ]  )     {      if     (  !  visited  [  i  ]  )      DFS  (  i       visited  );      }      }      // Returns true if given graph is connected else false      private     boolean     IsConnected  ()      {      boolean  []     visited     =     new     boolean  [  V  ]  ;      // Find all reachable vertices from first vertex      DFS  (  0       visited  );      // If set of reachable vertices includes all      // return true.      for     (  int     i     =     1  ;     i      <     V  ;     i  ++  )     {      if     (  visited  [  i  ]     ==     false  )      return     false  ;      }      return     true  ;      }      // This function assumes that edge (u v)      // exists in graph or not      public     void     ReverseDeleteMST  ()      {      // Sort edges in increasing order on basis of cost      Collections  .  sort  (  edges  );      int     mst_wt     =     0  ;     // Initialize weight of MST      System  .  out  .  println  (  'Edges in MST'  );      // Iterate through all sorted edges in      // decreasing order of weights      for     (  int     i     =     edges  .  size  ()     -     1  ;     i     >=     0  ;     i  --  )     {      int     u     =     edges  .  get  (  i  ).  u  ;      int     v     =     edges  .  get  (  i  ).  v  ;      // Remove edge from undirected graph      adj  [  u  ]  .  remove  (  adj  [  u  ]  .  indexOf  (  v  ));      adj  [  v  ]  .  remove  (  adj  [  v  ]  .  indexOf  (  u  ));      // Adding the edge back if removing it      // causes disconnection. In this case this      // edge becomes part of MST.      if     (  IsConnected  ()     ==     false  )     {      adj  [  u  ]  .  add  (  v  );      adj  [  v  ]  .  add  (  u  );      // This edge is part of MST      System  .  out  .  println  (  '('     +     u     +     ' '     +     v      +     ')'  );      mst_wt     +=     edges  .  get  (  i  ).  w  ;      }      }      System  .  out  .  println  (  'Total weight of MST is '      +     mst_wt  );      }      // Driver code      public     static     void     main  (  String  []     args  )      {      // create the graph given in above figure      int     V     =     9  ;      GFG     g     =     new     GFG  (  V  );      // making above shown graph      g  .  AddEdge  (  0       1       4  );      g  .  AddEdge  (  0       7       8  );      g  .  AddEdge  (  1       2       8  );      g  .  AddEdge  (  1       7       11  );      g  .  AddEdge  (  2       3       7  );      g  .  AddEdge  (  2       8       2  );      g  .  AddEdge  (  2       5       4  );      g  .  AddEdge  (  3       4       9  );      g  .  AddEdge  (  3       5       14  );      g  .  AddEdge  (  4       5       10  );      g  .  AddEdge  (  5       6       2  );      g  .  AddEdge  (  6       7       1  );      g  .  AddEdge  (  6       8       6  );      g  .  AddEdge  (  7       8       7  );      g  .  ReverseDeleteMST  ();      }   }   // This code is contributed by Prithi_Dey   
  Python3      # Python3 program to find Minimum Spanning Tree   # of a graph using Reverse Delete Algorithm   # Graph class represents a directed graph   # using adjacency list representation   class   Graph  :   def   __init__  (  self     v  ):   # No. of vertices   self  .  v   =   v   self  .  adj   =   [  0  ]   *   v   self  .  edges   =   []   for   i   in   range  (  v  ):   self  .  adj  [  i  ]   =   []   # function to add an edge to graph   def   addEdge  (  self     u  :   int     v  :   int     w  :   int  ):   self  .  adj  [  u  ]  .  append  (  v  )   # Add w to v’s list.   self  .  adj  [  v  ]  .  append  (  u  )   # Add w to v’s list.   self  .  edges  .  append  ((  w     (  u     v  )))   def   dfs  (  self     v  :   int     visited  :   list  ):   # Mark the current node as visited and print it   visited  [  v  ]   =   True   # Recur for all the vertices adjacent to   # this vertex   for   i   in   self  .  adj  [  v  ]:   if   not   visited  [  i  ]:   self  .  dfs  (  i     visited  )   # Returns true if graph is connected   # Returns true if given graph is connected else false   def   connected  (  self  ):   visited   =   [  False  ]   *   self  .  v   # Find all reachable vertices from first vertex   self  .  dfs  (  0     visited  )   # If set of reachable vertices includes all   # return true.   for   i   in   range  (  1     self  .  v  ):   if   not   visited  [  i  ]:   return   False   return   True   # This function assumes that edge (u v)   # exists in graph or not   def   reverseDeleteMST  (  self  ):   # Sort edges in increasing order on basis of cost   self  .  edges  .  sort  (  key   =   lambda   a  :   a  [  0  ])   mst_wt   =   0   # Initialize weight of MST   print  (  'Edges in MST'  )   # Iterate through all sorted edges in   # decreasing order of weights   for   i   in   range  (  len  (  self  .  edges  )   -   1     -  1     -  1  ):   u   =   self  .  edges  [  i  ][  1  ][  0  ]   v   =   self  .  edges  [  i  ][  1  ][  1  ]   # Remove edge from undirected graph   self  .  adj  [  u  ]  .  remove  (  v  )   self  .  adj  [  v  ]  .  remove  (  u  )   # Adding the edge back if removing it   # causes disconnection. In this case this   # edge becomes part of MST.   if   self  .  connected  ()   ==   False  :   self  .  adj  [  u  ]  .  append  (  v  )   self  .  adj  [  v  ]  .  append  (  u  )   # This edge is part of MST   print  (  '(   %d     %d   )'   %   (  u     v  ))   mst_wt   +=   self  .  edges  [  i  ][  0  ]   print  (  'Total weight of MST is'     mst_wt  )   # Driver Code   if   __name__   ==   '__main__'  :   # create the graph given in above figure   V   =   9   g   =   Graph  (  V  )   # making above shown graph   g  .  addEdge  (  0     1     4  )   g  .  addEdge  (  0     7     8  )   g  .  addEdge  (  1     2     8  )   g  .  addEdge  (  1     7     11  )   g  .  addEdge  (  2     3     7  )   g  .  addEdge  (  2     8     2  )   g  .  addEdge  (  2     5     4  )   g  .  addEdge  (  3     4     9  )   g  .  addEdge  (  3     5     14  )   g  .  addEdge  (  4     5     10  )   g  .  addEdge  (  5     6     2  )   g  .  addEdge  (  6     7     1  )   g  .  addEdge  (  6     8     6  )   g  .  addEdge  (  7     8     7  )   g  .  reverseDeleteMST  ()   # This code is contributed by   # sanjeev2552   
  C#      // C# program to find Minimum Spanning Tree   // of a graph using Reverse Delete Algorithm   using     System  ;   using     System.Collections.Generic  ;   // class to represent an edge   public     class     Edge     :     IComparable   <  Edge  >     {      public     int     u       v       w  ;      public     Edge  (  int     u       int     v       int     w  )      {      this  .  u     =     u  ;      this  .  v     =     v  ;      this  .  w     =     w  ;      }      public     int     CompareTo  (  Edge     other  )      {      return     this  .  w  .  CompareTo  (  other  .  w  );      }   }   // Graph class represents a directed graph   // using adjacency list representation   public     class     Graph     {      private     int     V  ;     // No. of vertices      private     List   <  int  >  []     adj  ;      private     List   <  Edge  >     edges  ;      public     Graph  (  int     v  )     // Constructor      {      V     =     v  ;      adj     =     new     List   <  int  >  [     v     ];      for     (  int     i     =     0  ;     i      <     v  ;     i  ++  )      adj  [  i  ]     =     new     List   <  int  >  ();      edges     =     new     List   <  Edge  >  ();      }      // function to Add an edge      public     void     AddEdge  (  int     u       int     v       int     w  )      {      adj  [  u  ].  Add  (  v  );     // Add w to v’s list.      adj  [  v  ].  Add  (  u  );     // Add w to v’s list.      edges  .  Add  (  new     Edge  (  u       v       w  ));      }      // function to perform dfs      private     void     DFS  (  int     v       bool  []     visited  )      {      // Mark the current node as visited and print it      visited  [  v  ]     =     true  ;      // Recur for all the vertices adjacent to      // this vertex      foreach  (  int     i     in     adj  [  v  ])      {      if     (  !  visited  [  i  ])      DFS  (  i       visited  );      }      }      // Returns true if given graph is connected else false      private     bool     IsConnected  ()      {      bool  []     visited     =     new     bool  [  V  ];      // Find all reachable vertices from first vertex      DFS  (  0       visited  );      // If set of reachable vertices includes all      // return true.      for     (  int     i     =     1  ;     i      <     V  ;     i  ++  )     {      if     (  visited  [  i  ]     ==     false  )      return     false  ;      }      return     true  ;      }      // This function assumes that edge (u v)      // exists in graph or not      public     void     ReverseDeleteMST  ()      {      // Sort edges in increasing order on basis of cost      edges  .  Sort  ();      int     mst_wt     =     0  ;     // Initialize weight of MST      Console  .  WriteLine  (  'Edges in MST'  );      // Iterate through all sorted edges in      // decreasing order of weights      for     (  int     i     =     edges  .  Count     -     1  ;     i     >=     0  ;     i  --  )     {      int     u     =     edges  [  i  ].  u  ;      int     v     =     edges  [  i  ].  v  ;      // Remove edge from undirected graph      adj  [  u  ].  Remove  (  v  );      adj  [  v  ].  Remove  (  u  );      // Adding the edge back if removing it      // causes disconnection. In this case this      // edge becomes part of MST.      if     (  IsConnected  ()     ==     false  )     {      adj  [  u  ].  Add  (  v  );      adj  [  v  ].  Add  (  u  );      // This edge is part of MST      Console  .  WriteLine  (  '({0} {1})'       u       v  );      mst_wt     +=     edges  [  i  ].  w  ;      }      }      Console  .  WriteLine  (  'Total weight of MST is {0}'        mst_wt  );      }   }   class     GFG     {      // Driver code      static     void     Main  (  string  []     args  )      {      // create the graph given in above figure      int     V     =     9  ;      Graph     g     =     new     Graph  (  V  );      // making above shown graph      g  .  AddEdge  (  0       1       4  );      g  .  AddEdge  (  0       7       8  );      g  .  AddEdge  (  1       2       8  );      g  .  AddEdge  (  1       7       11  );      g  .  AddEdge  (  2       3       7  );      g  .  AddEdge  (  2       8       2  );      g  .  AddEdge  (  2       5       4  );      g  .  AddEdge  (  3       4       9  );      g  .  AddEdge  (  3       5       14  );      g  .  AddEdge  (  4       5       10  );      g  .  AddEdge  (  5       6       2  );      g  .  AddEdge  (  6       7       1  );      g  .  AddEdge  (  6       8       6  );      g  .  AddEdge  (  7       8       7  );      g  .  ReverseDeleteMST  ();      }   }   // This code is contributed by cavi4762   
  JavaScript      // Javascript program to find Minimum Spanning Tree   // of a graph using Reverse Delete Algorithm   // Graph class represents a directed graph   // using adjacency list representation   class     Graph     {      // Constructor      constructor  (  V  )     {      this  .  V     =     V  ;      this  .  adj     =     [];      this  .  edges     =     [];      for     (  let     i     =     0  ;     i      <     V  ;     i  ++  )     {      this  .  adj  [  i  ]     =     [];      }      }          // function to add an edge to graph      addEdge  (  u       v       w  )     {      this  .  adj  [  u  ].  push  (  v  );  // Add w to v’s list.      this  .  adj  [  v  ].  push  (  u  );  // Add w to v’s list.      this  .  edges  .  push  ([  w       [  u       v  ]]);      }      DFS  (  v       visited  )     {      // Mark the current node as visited and print it      visited  [  v  ]     =     true  ;      for     (  const     i     of     this  .  adj  [  v  ])     {      if     (  !  visited  [  i  ])     {      this  .  DFS  (  i       visited  );      }      }      }      // Returns true if given graph is connected else false      isConnected  ()     {      const     visited     =     [];      for     (  let     i     =     0  ;     i      <     this  .  V  ;     i  ++  )     {      visited  [  i  ]     =     false  ;      }          // Find all reachable vertices from first vertex      this  .  DFS  (  0       visited  );          // If set of reachable vertices includes all      // return true.      for     (  let     i     =     1  ;     i      <     this  .  V  ;     i  ++  )     {      if     (  !  visited  [  i  ])     {      return     false  ;      }      }      return     true  ;      }      // This function assumes that edge (u v)      // exists in graph or not      reverseDeleteMST  ()     {          // Sort edges in increasing order on basis of cost      this  .  edges  .  sort  ((  a       b  )     =>     a  [  0  ]     -     b  [  0  ]);          let     mstWt     =     0  ;  // Initialize weight of MST          console  .  log  (  'Edges in MST'  );          // Iterate through all sorted edges in      // decreasing order of weights      for     (  let     i     =     this  .  edges  .  length     -     1  ;     i     >=     0  ;     i  --  )     {      const     [  u       v  ]     =     this  .  edges  [  i  ][  1  ];          // Remove edge from undirected graph      this  .  adj  [  u  ]     =     this  .  adj  [  u  ].  filter  (  x     =>     x     !==     v  );      this  .  adj  [  v  ]     =     this  .  adj  [  v  ].  filter  (  x     =>     x     !==     u  );          // Adding the edge back if removing it      // causes disconnection. In this case this       // edge becomes part of MST.      if     (  !  this  .  isConnected  ())     {      this  .  adj  [  u  ].  push  (  v  );      this  .  adj  [  v  ].  push  (  u  );          // This edge is part of MST      console  .  log  (  `(  ${  u  }     ${  v  }  )`  );      mstWt     +=     this  .  edges  [  i  ][  0  ];      }      }      console  .  log  (  `Total weight of MST is   ${  mstWt  }  `  );      }   }   // Driver code   function     main  ()   {      // create the graph given in above figure      var     V     =     9  ;      var     g     =     new     Graph  (  V  );      // making above shown graph      g  .  addEdge  (  0       1       4  );      g  .  addEdge  (  0       7       8  );      g  .  addEdge  (  1       2       8  );      g  .  addEdge  (  1       7       11  );      g  .  addEdge  (  2       3       7  );      g  .  addEdge  (  2       8       2  );      g  .  addEdge  (  2       5       4  );      g  .  addEdge  (  3       4       9  );      g  .  addEdge  (  3       5       14  );      g  .  addEdge  (  4       5       10  );      g  .  addEdge  (  5       6       2  );      g  .  addEdge  (  6       7       1  );      g  .  addEdge  (  6       8       6  );      g  .  addEdge  (  7       8       7  );      g  .  reverseDeleteMST  ();   }   main  ();   
    
  الإخراج   Edges in MST (3 4) (0 7) (2 3) (2 5) (0 1) (5 6) (2 8) (6 7) Total weight of MST is 37  
     التعقيد الزمني: O ((E*(V+E)) + E log E)    حيث E هو عدد الحواف.  
      تعقيد الفضاء: O(V+E)    حيث V هو عدد القمم و E هو عدد الحواف. نحن نستخدم قائمة الجوار لتخزين الرسم البياني لذلك نحتاج إلى مساحة متناسبة مع O(V+E).  
      ملحوظات :     
    التنفيذ أعلاه هو تطبيق بسيط/ساذج لخوارزمية الحذف العكسي ويمكن تحسينه إلى O(E log V (log log V)  ³ ) [مصدر :    اسبوع    ]. لكن هذا التعقيد الزمني الأمثل لا يزال أقل من    بريم    و    كروسكال    خوارزميات MST.  
  يعدل التنفيذ أعلاه الرسم البياني الأصلي. يمكننا إنشاء نسخة من الرسم البياني إذا كان من الضروري الاحتفاظ بالرسم البياني الأصلي.  
 
     
         إنشاء اختبار