تقييم شجرة التعبير
نظرا بسيطة شجرة التعبير تتكون من عوامل تشغيل ثنائية أساسية، مثل + - * و/ وبعض الأعداد الصحيحة تقوم بتقييم شجرة التعبير.
أمثلة:
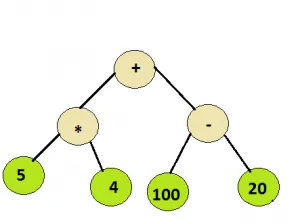
الممارسة الموصى بها شجرة التعبير جربه!مدخل: العقدة الجذرية للشجرة أدناه

الإخراج: 100
مدخل: العقدة الجذرية للشجرة أدناه
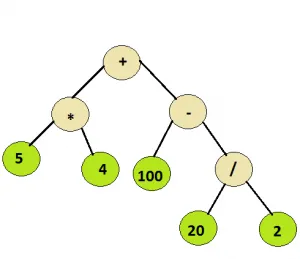
الإخراج: 110
يقترب: يعتمد أسلوب حل هذه المشكلة على الملاحظة التالية:
نظرًا لأن جميع العوامل في الشجرة ثنائية، فإن كل عقدة سيكون لها إما 0 أو 2 طفل. كما يمكن الاستدلال عليه من الأمثلة المذكورة أعلاه، ستظهر جميع قيم الأعداد الصحيحة في العقد الطرفية بينما تمثل العقد الداخلية العوامل.
ولذلك يمكننا أن نفعل الاجتياز الداخلي للشجرة الثنائية وتقييم التعبير ونحن نمضي قدما.
لتقييم شجرة بناء الجملة يمكن اتباع نهج عودي.
الخوارزمية:
- دع t تكون شجرة بناء الجملة
- إذا لم تكن فارغة
- إذا كان t.info هو المعامل إذن
- ارجع t.info
- آخر
- أ = حل (t.left)
- ب = حل(t.right)
- إرجاع عامل التشغيل B حيث يكون عامل التشغيل هو المعلومات الموجودة في t
وفيما يلي تنفيذ النهج المذكور أعلاه:
C++ // C++ program to evaluate an expression tree #include using namespace std ; // Class to represent the nodes of syntax tree class node { public : string info ; node * left = NULL * right = NULL ; node ( string x ) { info = x ; } }; // Utility function to return the integer value // of a given string int toInt ( string s ) { int num = 0 ; // Check if the integral value is // negative or not // If it is not negative generate the number // normally if ( s [ 0 ] != '-' ) for ( int i = 0 ; i < s . length (); i ++ ) num = num * 10 + ( int ( s [ i ]) -48 ); // If it is negative calculate the +ve number // first ignoring the sign and invert the // sign at the end else { for ( int i = 1 ; i < s . length (); i ++ ) num = num * 10 + ( int ( s [ i ]) -48 ); num = num * -1 ; } return num ; } // This function receives a node of the syntax tree // and recursively evaluates it int eval ( node * root ) { // empty tree if ( ! root ) return 0 ; // leaf node i.e an integer if ( ! root -> left && ! root -> right ) return toInt ( root -> info ); // Evaluate left subtree int l_val = eval ( root -> left ); // Evaluate right subtree int r_val = eval ( root -> right ); // Check which operator to apply if ( root -> info == '+' ) return l_val + r_val ; if ( root -> info == '-' ) return l_val - r_val ; if ( root -> info == '*' ) return l_val * r_val ; return l_val / r_val ; } //driver function to check the above program int main () { // create a syntax tree node * root = new node ( '+' ); root -> left = new node ( '*' ); root -> left -> left = new node ( '5' ); root -> left -> right = new node ( '-4' ); root -> right = new node ( '-' ); root -> right -> left = new node ( '100' ); root -> right -> right = new node ( '20' ); cout < < eval ( root ) < < endl ; delete ( root ); root = new node ( '+' ); root -> left = new node ( '*' ); root -> left -> left = new node ( '5' ); root -> left -> right = new node ( '4' ); root -> right = new node ( '-' ); root -> right -> left = new node ( '100' ); root -> right -> right = new node ( '/' ); root -> right -> right -> left = new node ( '20' ); root -> right -> right -> right = new node ( '2' ); cout < < eval ( root ); return 0 ; }
Java // Java program to evaluate expression tree import java.lang.* ; class GFG { Node root ; // Class to represent the nodes of syntax tree public static class Node { String data ; Node left right ; Node ( String d ) { data = d ; left = null ; right = null ; } } private static int toInt ( String s ) { int num = 0 ; // Check if the integral value is // negative or not // If it is not negative generate // the number normally if ( s . charAt ( 0 ) != '-' ) for ( int i = 0 ; i < s . length (); i ++ ) num = num * 10 + (( int ) s . charAt ( i ) - 48 ); // If it is negative calculate the +ve number // first ignoring the sign and invert the // sign at the end else { for ( int i = 1 ; i < s . length (); i ++ ) num = num * 10 + (( int )( s . charAt ( i )) - 48 ); num = num * - 1 ; } return num ; } // This function receives a node of the syntax // tree and recursively evaluate it public static int evalTree ( Node root ) { // Empty tree if ( root == null ) return 0 ; // Leaf node i.e an integer if ( root . left == null && root . right == null ) return toInt ( root . data ); // Evaluate left subtree int leftEval = evalTree ( root . left ); // Evaluate right subtree int rightEval = evalTree ( root . right ); // Check which operator to apply if ( root . data . equals ( '+' )) return leftEval + rightEval ; if ( root . data . equals ( '-' )) return leftEval - rightEval ; if ( root . data . equals ( '*' )) return leftEval * rightEval ; return leftEval / rightEval ; } // Driver code public static void main ( String [] args ) { // Creating a sample tree Node root = new Node ( '+' ); root . left = new Node ( '*' ); root . left . left = new Node ( '5' ); root . left . right = new Node ( '-4' ); root . right = new Node ( '-' ); root . right . left = new Node ( '100' ); root . right . right = new Node ( '20' ); System . out . println ( evalTree ( root )); root = null ; // Creating a sample tree root = new Node ( '+' ); root . left = new Node ( '*' ); root . left . left = new Node ( '5' ); root . left . right = new Node ( '4' ); root . right = new Node ( '-' ); root . right . left = new Node ( '100' ); root . right . right = new Node ( '/' ); root . right . right . left = new Node ( '20' ); root . right . right . right = new Node ( '2' ); System . out . println ( evalTree ( root )); } } // This code is contributed by Ankit Gupta
Python3 # Python program to evaluate expression tree # Class to represent the nodes of syntax tree class node : def __init__ ( self value ): self . left = None self . data = value self . right = None # This function receives a node of the syntax tree # and recursively evaluate it def evaluateExpressionTree ( root ): # empty tree if root is None : return 0 # leaf node if root . left is None and root . right is None : return int ( root . data ) # evaluate left tree left_sum = evaluateExpressionTree ( root . left ) # evaluate right tree right_sum = evaluateExpressionTree ( root . right ) # check which operation to apply if root . data == '+' : return left_sum + right_sum elif root . data == '-' : return left_sum - right_sum elif root . data == '*' : return left_sum * right_sum else : return left_sum // right_sum # Driver function to test above problem if __name__ == '__main__' : # creating a sample tree root = node ( '+' ) root . left = node ( '*' ) root . left . left = node ( '5' ) root . left . right = node ( '-4' ) root . right = node ( '-' ) root . right . left = node ( '100' ) root . right . right = node ( '20' ) print ( evaluateExpressionTree ( root )) root = None # creating a sample tree root = node ( '+' ) root . left = node ( '*' ) root . left . left = node ( '5' ) root . left . right = node ( '4' ) root . right = node ( '-' ) root . right . left = node ( '100' ) root . right . right = node ( '/' ) root . right . right . left = node ( '20' ) root . right . right . right = node ( '2' ) print ( evaluateExpressionTree ( root )) # This code is contributed by Harshit Sidhwa
C# // C# program to evaluate expression tree using System ; public class GFG { // Class to represent the nodes of syntax tree public class Node { public String data ; public Node left right ; public Node ( String d ) { data = d ; left = null ; right = null ; } } private static int toInt ( String s ) { int num = 0 ; // Check if the integral value is // negative or not // If it is not negative generate // the number normally if ( s [ 0 ] != '-' ) for ( int i = 0 ; i < s . Length ; i ++ ) num = num * 10 + (( int ) s [ i ] - 48 ); // If it is negative calculate the +ve number // first ignoring the sign and invert the // sign at the end else { for ( int i = 1 ; i < s . Length ; i ++ ) num = num * 10 + (( int ) ( s [ i ]) - 48 ); num = num * - 1 ; } return num ; } // This function receives a node of the syntax // tree and recursively evaluate it public static int evalTree ( Node root ) { // Empty tree if ( root == null ) return 0 ; // Leaf node i.e an integer if ( root . left == null && root . right == null ) return toInt ( root . data ); // Evaluate left subtree int leftEval = evalTree ( root . left ); // Evaluate right subtree int rightEval = evalTree ( root . right ); // Check which operator to apply if ( root . data . Equals ( '+' )) return leftEval + rightEval ; if ( root . data . Equals ( '-' )) return leftEval - rightEval ; if ( root . data . Equals ( '*' )) return leftEval * rightEval ; return leftEval / rightEval ; } // Driver code public static void Main ( String [] args ) { // Creating a sample tree Node root = new Node ( '+' ); root . left = new Node ( '*' ); root . left . left = new Node ( '5' ); root . left . right = new Node ( '-4' ); root . right = new Node ( '-' ); root . right . left = new Node ( '100' ); root . right . right = new Node ( '20' ); Console . WriteLine ( evalTree ( root )); root = null ; // Creating a sample tree root = new Node ( '+' ); root . left = new Node ( '*' ); root . left . left = new Node ( '5' ); root . left . right = new Node ( '4' ); root . right = new Node ( '-' ); root . right . left = new Node ( '100' ); root . right . right = new Node ( '/' ); root . right . right . left = new Node ( '20' ); root . right . right . right = new Node ( '2' ); Console . WriteLine ( evalTree ( root )); } } // This code is contributed by umadevi9616
JavaScript < script > // javascript program to evaluate expression tree var root ; // Class to represent the nodes of syntax tree class Node { constructor ( val ) { this . data = val ; this . left = null ; this . right = null ; } } function toInt ( s ) { var num = 0 ; // Check if the integral value is // negative or not // If it is not negative generate // the number normally if ( s . charAt ( 0 ) != '-' ) for ( i = 0 ; i < s . length ; i ++ ) num = num * 10 + ( s . charCodeAt ( i ) - 48 ); // If it is negative calculate the +ve number // first ignoring the sign and invert the // sign at the end else { for ( i = 1 ; i < s . length ; i ++ ) num = num * 10 + ( s . charCodeAt ( i ) - 48 ); num = num * - 1 ; } return num ; } // This function receives a node of the syntax // tree and recursively evaluate it function evalTree ( root ) { // Empty tree if ( root == null ) return 0 ; // Leaf node i.e an integer if ( root . left == null && root . right == null ) return toInt ( root . data ); // Evaluate left subtree var leftEval = evalTree ( root . left ); // Evaluate right subtree var rightEval = evalTree ( root . right ); // Check which operator to apply if ( root . data === ( '+' )) return leftEval + rightEval ; if ( root . data === ( '-' )) return leftEval - rightEval ; if ( root . data === ( '*' )) return leftEval * rightEval ; return leftEval / rightEval ; } // Driver code // Creating a sample tree var root = new Node ( '+' ); root . left = new Node ( '*' ); root . left . left = new Node ( '5' ); root . left . right = new Node ( '-4' ); root . right = new Node ( '-' ); root . right . left = new Node ( '100' ); root . right . right = new Node ( '20' ); document . write ( evalTree ( root )); root = null ; // Creating a sample tree root = new Node ( '+' ); root . left = new Node ( '*' ); root . left . left = new Node ( '5' ); root . left . right = new Node ( '4' ); root . right = new Node ( '-' ); root . right . left = new Node ( '100' ); root . right . right = new Node ( '/' ); root . right . right . left = new Node ( '20' ); root . right . right . right = new Node ( '2' ); document . write ( '
' + evalTree ( root )); // This code is contributed by gauravrajput1 < /script>
الإخراج
60 110
تعقيد الوقت: O(n) حيث تتم زيارة كل عقدة مرة واحدة.
المساحة المساعدة: على)