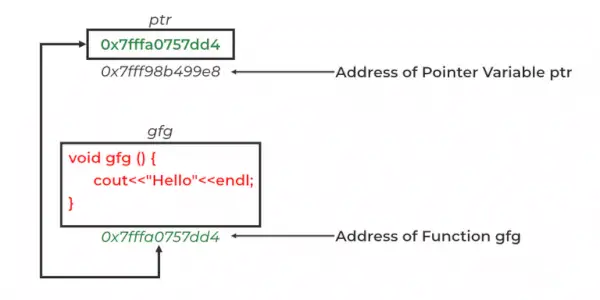
ПОПЕРЕДНЄ ЗАМОВЛЕННЯ ОБХОДУ БІНАРНОГО ДЕРЕВА - TECHCODEVIEW.COM

Обхід попереднього замовлення визначається як вид обхід дерева який дотримується політики Root-Left-Right, де:

Першим відвідується кореневий вузол піддерева.

Потім виконується обхід лівого піддерева.

Нарешті, праве піддерево обходиться.

Обхід попереднього замовлення

Алгоритм попереднього обходу бінарного дерева

Алгоритм попереднього обходу показаний таким чином:

Попереднє замовлення (корінь):

Виконуйте кроки 2-4, доки root не стане != NULL

Записати корінь -> дані

Попереднє замовлення (корінь -> ліворуч)

Попереднє замовлення (root -> right)

Кінцева петля

Як працює попередній обхід бінарного дерева?

Розглянемо таке дерево:

Приклад бінарного дерева

Якщо ми виконуємо попередній обхід у цьому бінарному дереві, то обхід буде таким:

Крок 1: Спочатку буде відвідано корінь, тобто вузол 1.

Відвідується вузол 1

Крок 2: Після цього перейдіть у ліве піддерево. Тепер відвідується корінь лівого піддерева, тобто відвідується вузол 2.

Відвідується вузол 2

крок 3: Знову проходить ліве піддерево вузла 2 і відвідується корінь цього піддерева, тобто відвідується вузол 4.

Вузол 4 відвідується

крок 4: Немає піддерева 4, і відвідується ліве піддерево вузла 2. Таким чином, тепер буде пройдено праве піддерево вузла 2 і буде відвідано корінь цього піддерева, тобто вузол 5.

Вузол 5 відвідується

крок 5: Відвідується ліве піддерево вузла 1. Таким чином, тепер буде пройдено праве піддерево вузла 1 і відвідано кореневий вузол, тобто вузол 3.

Відвідується вузол 3

Крок 6: Вузол 3 не має лівого піддерева. Таким чином, буде проведено обхід правого піддерева та відвідано корінь піддерева, тобто вузол 6. Після цього немає вузла, який ще не пройдено. Так обхід закінчується.

Відвідується все дерево

Отже, порядок обходу вузлів такий 1 -> 2 -> 4 -> 5 -> 3 -> 6 .

Програма для здійснення попереднього обходу бінарного дерева

Нижче наведено реалізацію коду обходу попереднього замовлення:

C++

  // C++ program for preorder traversals #include  using namespace std; // Structure of a Binary Tree Node struct Node {  int data;  struct Node *left, *right;  Node(int v)  {  data = v;  left = right = NULL;  } }; // Function to print preorder traversal void printPreorder(struct Node* node) {  if (node == NULL)  return;  // Deal with the node  cout  < < node->даних < < ' ';  // Recur on left subtree  printPreorder(node->ліворуч);  // Повторюється в правому піддереві printPreorder(node->right); } // Код драйвера int main() { struct Node* root = new Node(1);  root->left = новий вузол (2);  root->right = новий вузол (3);  root->left->left = новий вузол(4);  root->left->right = новий вузол(5);  root->right->right = новий вузол (6);  // Виклик функції cout < < 'Preorder traversal of binary tree is: 
';  printPreorder(root);  return 0; }

Java

  // Java program for preorder traversals class Node {  int data;  Node left, right;  public Node(int item) {  data = item;  left = right = null;  } } class BinaryTree {  Node root;  BinaryTree() {  root = null;  }  // Function to print preorder traversal  void printPreorder(Node node) {  if (node == null)  return;  // Deal with the node  System.out.print(node.data + ' ');  // Recur on left subtree  printPreorder(node.left);  // Recur on right subtree  printPreorder(node.right);  }  // Driver code  public static void main(String[] args) {  BinaryTree tree = new BinaryTree();  // Constructing the binary tree  tree.root = new Node(1);  tree.root.left = new Node(2);  tree.root.right = new Node(3);  tree.root.left.left = new Node(4);  tree.root.left.right = new Node(5);  tree.root.right.right = new Node(6);  // Function call  System.out.println('Preorder traversal of binary tree is: ');  tree.printPreorder(tree.root);  } }

Python3

  # Python program for preorder traversals # Structure of a Binary Tree Node class Node: def __init__(self, v): self.data = v self.left = None self.right = None # Function to print preorder traversal def printPreorder(node): if node is None: return # Deal with the node print(node.data, end=' ') # Recur on left subtree printPreorder(node.left) # Recur on right subtree printPreorder(node.right) # Driver code if __name__ == '__main__': root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) root.right.right = Node(6) # Function call print('Preorder traversal of binary tree is:') printPreorder(root)

  // C# program for preorder traversals using System; // Structure of a Binary Tree Node public class Node {  public int data;  public Node left, right;  public Node(int v)  {  data = v;  left = right = null;  } } // Class to print preorder traversal public class BinaryTree {  // Function to print preorder traversal  public static void printPreorder(Node node)  {  if (node == null)  return;  // Deal with the node  Console.Write(node.data + ' ');  // Recur on left subtree  printPreorder(node.left);  // Recur on right subtree  printPreorder(node.right);  }  // Driver code  public static void Main()  {  Node root = new Node(1);  root.left = new Node(2);  root.right = new Node(3);  root.left.left = new Node(4);  root.left.right = new Node(5);  root.right.right = new Node(6);  // Function call  Console.WriteLine(  'Preorder traversal of binary tree is: ');  printPreorder(root);  } } // This code is contributed by Susobhan Akhuli

Javascript

  // Structure of a Binary Tree Node class Node {  constructor(v) {  this.data = v;  this.left = null;  this.right = null;  } } // Function to print preorder traversal function printPreorder(node) {  if (node === null) {  return;  }  // Deal with the node  console.log(node.data);  // Recur on left subtree  printPreorder(node.left);  // Recur on right subtree  printPreorder(node.right); } // Driver code function main() {  const root = new Node(1);  root.left = new Node(2);  root.right = new Node(3);  root.left.left = new Node(4);  root.left.right = new Node(5);  root.right.right = new Node(6);  // Function call  console.log('Preorder traversal of binary tree is:');  printPreorder(root); } main();

Вихід

Preorder traversal of binary tree is: 1 2 4 5 3 6

Пояснення:

Як працює обхід попереднього замовлення

Аналіз складності:

Часова складність: O(N), де N - загальна кількість вузлів. Тому що він проходить усі вузли принаймні один раз.
Допоміжний простір:

О(1) якщо простір стеку рекурсії не розглядається.
інакше, O(h) де h – висота дерева
У гіршому випадку ч може бути таким же, як Н (коли дерево перекошене)
У кращому випадку ч може бути таким же, як спокійний (коли дерево є повним деревом)