ШАБЛОН ФІЛОТАКСИСУ В PYTHON | РОЗДІЛ АЛГОРИТМІЧНОЇ БОТАНІКИ

Філотаксис/філотаксис — це розташування листя на стеблі рослини, а філотактичні спіралі утворюють особливий клас візерунків у природі. Саме слово походить від грецького phullon, що означає «лист», і taxis, що означає «композиція». Основні квіткові філотаксичні композиції включають:

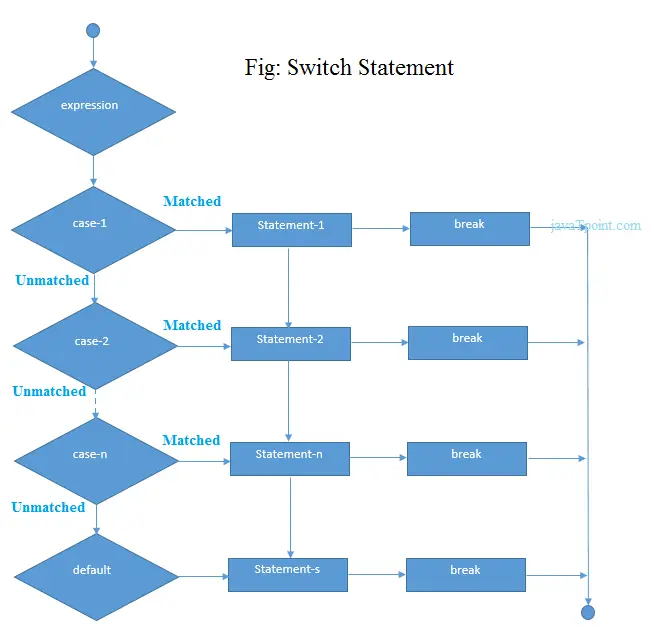
1. Спіральний філотаксис -

У спіральній філотаксії окремі квіткові органи створюються в регулярний проміжок часу з однаковим розбіжним кутом. Розбіжний кут у квітці зі спіральною філотаксією становить приблизно 137,5 градусів, що вказує на візерунок, який слідує

Ряд Фібоначчі

.На зображенні нижче показано спіральні візерунки філотаксії, які мають спіральні візерунки як за годинниковою стрілкою, так і проти неї.

Шаблон філотаксису в Python | Розділ алгоритмічної ботаніки

Важливі моменти, на які слід звернути увагу:

Ряди Фібоначчі зазвичай описують спіралі, які зустрічаються в природі. Він обчислюється як ряд, де сума попередньої пари чисел дорівнює наступному числу в ряді. Серія 1 1 2 3 5 8 13 21 34 55 89 … .
Насправді існує один набір спіралей, спрямованих за годинниковою стрілкою, а інший – проти годинникової стрілки.
Спіралі квіткових органів слідують за чисельником і знаменником набору зміщених чисел Фібоначчі (1/2 1/3 2/5 3/8 5/13 8/21 13/34 …). Чисельник — це кількість разів або поворотів навколо осі, щоб повернутися до початку початку. Знаменник вказує на кількість органів, запущених під час поворотів. Тому 2/5 означатиме 2 повороти навколо осі та 5 органів для повернення до початку координат.
наприклад, у сосни ми маємо (2 3) (5 3) і (5 8) філотаксиси в capituli знайдені пари (21 34) (55 34) (55 89) і (89 144), а на ананасах з шестикутною лускою знайдені триплети (8 13 21) або (13 21 34) залежно від від розміру зразків.
Переважання послідовності Фібоначчі у філотаксисі часто називають «таємницею філотаксису».

Інші типи квіткових філотаксичних композицій:

2. Філотаксис мутовчастий 3. Філотаксис простомутовчастий 4. Філотаксис складномутовчастий і 5. Філотаксис неправильної форми

Формування патерну : Резюме

Красиве розташування листя в деяких рослинах, які називаються філотаксисом, підкоряється ряду тонких математичних залежностей. Наприклад, суцвіття в головці соняшнику утворюють дві протилежно спрямовані спіралі: 55 з них за годинниковою стрілкою і 34 проти годинникової стрілки. Дивно

Ці числа є послідовними числами Фібоначчі.
Співвідношення альтернативних чисел Фібоначчі задаються конвергентами до φ^(-2), де φ є золотого перетину і кажуть, що вимірюють частку повороту між послідовними листками на стеблі рослини:
наприклад: 1/2 для в’яза та липи 1/3 для бука та ліщини 2/5 для дуба та яблуні 3/8 для тополі та троянди 5/13 для верби та мигдалю тощо.
Кожен новий лист на стеблі рослини розташований під певним кутом до попереднього, і цей кут є постійним між листками: зазвичай близько 137,5 градусів.

Тобто, якщо ви подивіться на рослину зверху вниз і виміряєте кут, утворений між лінією, проведеною від стебла до листка, і відповідною лінією для наступного листка, ви побачите, що зазвичай існує фіксований кут, який називається кутом розходження. Тут нас цікавить Спіральна філотаксія, і ми будемо кодувати, щоб сформувати візерунок Спіральна філотаксія на Python, використовуючи черепахову графіку.

Розробка коду

Ми закодуємо дві функції, одну для малювання візерунка філотаксії, а іншу для малювання пелюсток.
Пелюстки потрібно малювати лише після того, як шаблон філотаксису буде завершено. Тому ми викличемо функцію drawPetal() зсередини функції drawPhyllPattern() з останніми координатами x & y, відвіданими після малювання шаблону філотаксису.
Функція drawPetal() намалює пелюстки за допомогою черепахових функцій і функцій Програмування Turtle .

Щоб закодувати схему філотаксису, нам потрібно дотримуватися таких рівнянь:

 x = r*cos(θ)   
 y = r*sin(θ)   
  
 r θ can also vary - so the to form phyllotactic pattern we substitutethe cartesian form   
 by polar form:   
  
 r = c*sqrt(n)   
 θ = n*137.508°   
    Reduces the problem to optimal packing on a disc so   
  r = c*sqrt(n) is from the area of the circle   
  Area = πr² and n fills the Area in some units   
  c1 * n/π = r² c is 1/sqrt(c1/π)   
 So r = some constant c * sqrt(n)   
     Псевдокод: шаблон філотаксису    
  IMPORT MODULES ( MATH TURTLE )   
  
 FUNCTION - DrawPhyllotaxisPattern( turtle t length petalstart angle = 137.508 size cspread)   
  turtleColor('Black')   
  FillColor(''Orange')   
  Convert angle to radians (Φ)   
  initialize ( xcenterycenter ) = ( 00 )   
  Drawing the Pattern Starts:   
  For n in Range ( 0t ):   
  r = cspread * sqrt(n)   
  θ = n * Φ   
  
  x = r * cos(θ) + xcenter   
  y = r * sin(θ) + ycenter   
  
  TURTLE POSITION(xy)   
  START DRAWING():   
  if Drawing pattern ends:   
  DrawFlowerPetals()   
     
 FUNCTION - DrawFlowerPetals(Turtle x coordinate y coordinate)   
  DRAW using Turtle methods   
  
 Create Turtle = gfg   
 Call DrawPhyllotaxisPattern( gfg t length petalstart angle = 137.508 size cspread)   
  
 END   
 Python Pattern A      import   math   import   turtle   def   drawPhyllPattern  (  turtle     t     petalstart     angle   =   137.508     size   =   2     cspread   =   4   ):      '''print a pattern of circles using spiral phyllotactic data'''   # initialize position   # turtle.pen(outline=1 pencolor='black' fillcolor='orange')   turtle  .  color  (  'black'  )   turtle  .  fillcolor  (  'orange'  )   phi   =   angle   *   (   math  .  pi   /   180.0   )   #we convert to radian   xcenter   =   0.0   ycenter   =   0.0   # for loops iterate in this case from the first value until  < 4 so   for   n   in   range   (  0     t  ):   r   =   cspread   *   math  .  sqrt  (  n  )   theta   =   n   *   phi   x   =   r   *   math  .  cos  (  theta  )   +   xcenter   y   =   r   *   math  .  sin  (  theta  )   +   ycenter   # move the turtle to that position and draw    turtle  .  up  ()   turtle  .  setpos  (  x     y  )   turtle  .  down  ()   # orient the turtle correctly   turtle  .  setheading  (  n   *   angle  )   if   n   >   petalstart  -  1  :   turtle  .  color  (  'yellow'  )   drawPetal  (  turtle     x     y  )   else  :   turtle  .  stamp  ()   def   drawPetal  (  turtle     x     y   ):   turtle  .  penup  ()   turtle  .  goto  (  x     y  )   turtle  .  pendown  ()   turtle  .  color  (  'black'  )   turtle  .  fillcolor  (  'yellow'  )   turtle  .  begin_fill  ()   turtle  .  right  (  20  )   turtle  .  forward  (  70  )   turtle  .  left  (  40  )   turtle  .  forward  (  70  )   turtle  .  left  (  140  )   turtle  .  forward  (  70  )   turtle  .  left  (  40  )   turtle  .  forward  (  70  )   turtle  .  penup  ()   turtle  .  end_fill  ()   # this is needed to complete the last petal   gfg   =   turtle  .  Turtle  ()   gfg  .  shape  (  'turtle'  )   gfg  .  speed  (  0  )   # make the turtle go as fast as possible   drawPhyllPattern  (  gfg     200     160     137.508   )   gfg  .  penup  ()   gfg  .  forward  (  1000  )   
  Python Pattern B      import   math   import   turtle   def   drawPhyllotacticPattern  (   t     petalstart     angle   =   137.508     size   =   2     cspread   =   4   ):      '''print a pattern of circles using spiral phyllotactic data'''   # initialize position   turtle  .  pen  (  outline  =  1     pencolor  =  'black'     fillcolor  =  'orange'  )   # turtle.color('orange')   phi   =   angle   *   (   math  .  pi   /   180.0   )   xcenter   =   0.0   ycenter   =   0.0   # for loops iterate in this case from the first value until  < 4 so   for   n   in   range   (  0     t  ):   r   =   cspread   *   math  .  sqrt  (  n  )   theta   =   n   *   phi   x   =   r   *   math  .  cos  (  theta  )   +   xcenter   y   =   r   *   math  .  sin  (  theta  )   +   ycenter   # move the turtle to that position and draw    turtle  .  up  ()   turtle  .  setpos  (  x     y  )   turtle  .  down  ()   # orient the turtle correctly   turtle  .  setheading  (  n   *   angle  )   if   n   >   petalstart  -  1  :   #turtle.color('yellow')   drawPetal  (  x     y  )   else  :   turtle  .  stamp  ()   def   drawPetal  (   x     y   ):   turtle  .  up  ()   turtle  .  setpos  (  x     y  )   turtle  .  down  ()   turtle  .  begin_fill  ()   #turtle.fill(True)   turtle  .  pen  (  outline  =  1     pencolor  =  'black'     fillcolor  =  'yellow'  )   turtle  .  right  (  20  )   turtle  .  forward  (  100  )   turtle  .  left  (  40  )   turtle  .  forward  (  100  )   turtle  .  left  (  140  )   turtle  .  forward  (  100  )   turtle  .  left  (  40  )   turtle  .  forward  (  100  )   turtle  .  up  ()   turtle  .  end_fill  ()   # this is needed to complete the last petal   turtle  .  shape  (  'turtle'  )   turtle  .  speed  (  0  )   # make the turtle go as fast as possible   drawPhyllotacticPattern  (   200     160     137.508     4     10   )   turtle  .  exitonclick  ()   # lets you x out of the window when outside of idle   
       Вихід:    
  Шаблони філотаксису.  
       
         Створіть вікторину