Логістична регресія в програмуванні R

Логістична регресія в програмуванні R — це алгоритм класифікації, який використовується для визначення ймовірності успіху та невдачі події. Логістична регресія використовується, коли залежна змінна є двійковою (0/1, Істина/Неправда, Так/Ні) за своєю природою. Функція logit використовується як функція зв’язку в біноміальному розподілі.
Імовірність бінарної змінної результату можна передбачити за допомогою методу статистичного моделювання, відомого як логістична регресія. Він широко використовується в багатьох галузях промисловості, включаючи маркетинг, фінанси, соціальні науки та медичні дослідження.
Логістична функція, яку зазвичай називають сигмоподібною функцією, є основною ідеєю, що лежить в основі логістичної регресії. Ця сигмоїдна функція використовується в логістичній регресії для опису кореляції між змінними предиктора та ймовірністю бінарного результату.

Логістична регресія в програмуванні R
Логістична регресія також відома як Біноміальна логістична регресія . Він заснований на сигмоїдній функції, де вихід є ймовірністю, а вхід може бути від -нескінченності до +нескінченності.
Теорія
Логістична регресія також відома як узагальнена лінійна модель. Оскільки воно використовується як метод класифікації для прогнозування якісної відповіді, значення y коливається від 0 до 1 і може бути представлене таким рівнянням:

Логістична регресія в програмуванні R
стор це ймовірність характеристики, що цікавить. Коефіцієнт шансів визначається як ймовірність успіху в порівнянні з ймовірністю невдачі. Це ключове представлення коефіцієнтів логістичної регресії та може приймати значення від 0 до нескінченності. Співвідношення шансів 1 — це коли ймовірність успіху дорівнює ймовірності невдачі. Співвідношення шансів 2 означає, що ймовірність успіху вдвічі перевищує ймовірність невдачі. Коефіцієнт шансів 0,5 — це коли ймовірність невдачі вдвічі перевищує ймовірність успіху.
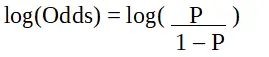
Логістична регресія в програмуванні R
Оскільки ми працюємо з біноміальним розподілом (залежна змінна), нам потрібно вибрати функцію зв’язку, яка найкраще підходить для цього розподілу.
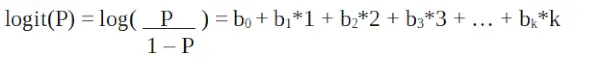
Логістична регресія в програмуванні R
Це функція logit . У наведеному вище рівнянні круглу дужку вибрано для максимізації ймовірності спостереження значень вибірки, а не для мінімізації суми квадратів помилок (як у звичайної регресії). Логіт також відомий як журнал шансів. Функція logit має бути лінійно пов’язана з незалежними змінними. Це з рівняння A, де ліва частина є лінійною комбінацією x. Це схоже на припущення МНК про те, що y має лінійну залежність від x. Змінні b0, b1, b2 … тощо невідомі та повинні бути оцінені на основі доступних даних навчання. У моделі логістичної регресії множення b1 на одиницю змінює logit на b0. Зміни P через зміну на одну одиницю залежатимуть від помноженого значення. Якщо b1 додатне, то P збільшиться, а якщо b1 від’ємне, то P зменшиться.
Набір даних
mtcars (Motor Trend Car Road Test) містить споживання палива, продуктивність і 10 аспектів дизайну автомобіля для 32 автомобілів. Він поставляється з попередньо встановленим dplyr пакет в R.
Р
# Installing the package> install.packages> (> 'dplyr'> )> # Loading package> library> (dplyr)> # Summary of dataset in package> summary> (mtcars)> |
Виконання логістичної регресії для набору даних
Логістична регресія реалізована в R за допомогою glm() шляхом навчання моделі за допомогою функцій або змінних у наборі даних.
Р
# Installing the package> # For Logistic regression> install.packages> (> 'caTools'> )> # For ROC curve to evaluate model> install.packages> (> 'ROCR'> )> > # Loading package> library> (caTools)> library> (ROCR)> |
Поділ даних
Р
# Splitting dataset> split <-> sample.split> (mtcars, SplitRatio = 0.8)> split> train_reg <-> subset> (mtcars, split ==> 'TRUE'> )> test_reg <-> subset> (mtcars, split ==> 'FALSE'> )> # Training model> logistic_model <-> glm> (vs ~ wt + disp,> > data = train_reg,> > family => 'binomial'> )> logistic_model> # Summary> summary> (logistic_model)> |
Вихід:
Call: glm(formula = vs ~ wt + disp, family = 'binomial', data = train_reg) Deviance Residuals: Min 1Q Median 3Q Max -1.6552 -0.4051 0.4446 0.6180 1.9191 Coefficients: Estimate Std. Error z value Pr(>|z|) (Перетин) 1,58781 2,60087 0,610 0,5415 вага 1,36958 1,60524 0,853 0,3936 дисп -0,02969 0,01577 -1,882 0,0598 . --- Означ. коди: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1 (Параметр дисперсії для біноміального сімейства приймається рівним 1) Нульове відхилення: 34,617 на 24 ступенях свободи Залишкове відхилення: 20,212 на 22 ступені свободи AIC: 26,212 Кількість ітерацій оцінки Фішера: 6
- Виклик: відображається виклик функції, який використовується для відповідності моделі логістичної регресії, разом із інформацією про сімейство, формулу та дані. Залишки відхилень: це залишки відхилень, які вимірюють ступінь відповідності моделі. Вони означають розбіжності між фактичними відповідями та ймовірністю, передбаченою моделлю логістичної регресії. Коефіцієнти: ці коефіцієнти в логістичній регресії представляють логарифмічні шанси або логіт змінної відповіді. Стандартні похибки, пов’язані з оціненими коефіцієнтами, наведені в стандартній таблиці. Стовпець помилок. Коди значущості: Рівень значущості кожної змінної предиктора позначається кодами значущості. Параметр дисперсії: у логістичній регресії параметр дисперсії служить параметром масштабування для біноміального розподілу. У цьому випадку встановлено значення 1, що вказує на те, що припущена дисперсія дорівнює 1. Нульове відхилення: нульове відхилення обчислює відхилення моделі, коли враховується лише перехоплення. Він символізує відхилення, яке буде результатом моделі без предикторів. Залишкове відхилення: Залишкове відхилення обчислює відхилення моделі після встановлення предикторів. Він означає залишкове відхилення після врахування предикторів. AIC: інформаційний критерій Akaike (AIC), який враховує кількість предикторів, є показником відповідності моделі. Він карає більш складні моделі, щоб запобігти надмірному оснащенню. Краще підігнані моделі позначаються нижчими значеннями AIC. Кількість ітерацій оцінки Фішера: кількість ітерацій, необхідних процедурі оцінки Фішера для оцінки параметрів моделі, вказується кількістю ітерацій.
Прогнозуйте тестові дані на основі моделі
Р
predict_reg <-> predict> (logistic_model,> > test_reg, type => 'response'> )> predict_reg> |
Вихід:
Hornet Sportabout Merc 280C Merc 450SE Chrysler Imperial 0.01226166 0.78972164 0.26380531 0.01544309 AMC Javelin Camaro Z28 Ford Pantera L 0.06104267 0.02807992 0.01107943
Р
# Changing probabilities> predict_reg <-> ifelse> (predict_reg>0,5, 1, 0)>> # Evaluating model accuracy> # using confusion matrix> table> (test_reg$vs, predict_reg)> missing_classerr <-> mean> (predict_reg != test_reg$vs)> print> (> paste> (> 'Accuracy ='> , 1 - missing_classerr))> # ROC-AUC Curve> ROCPred <-> prediction> (predict_reg, test_reg$vs)> ROCPer <-> performance> (ROCPred, measure => 'tpr'> ,> > x.measure => 'fpr'> )> auc <-> performance> (ROCPred, measure => 'auc'> )> auc <- [email protected][[1]]> auc> # Plotting curve> plot> (ROCPer)> plot> (ROCPer, colorize => TRUE> ,> > print.cutoffs.at => seq> (0.1, by = 0.1),> > main => 'ROC CURVE'> )> abline> (a = 0, b = 1)> auc <-> round> (auc, 4)> legend> (.6, .4, auc, title => 'AUC'> , cex = 1)> |
Вихід:
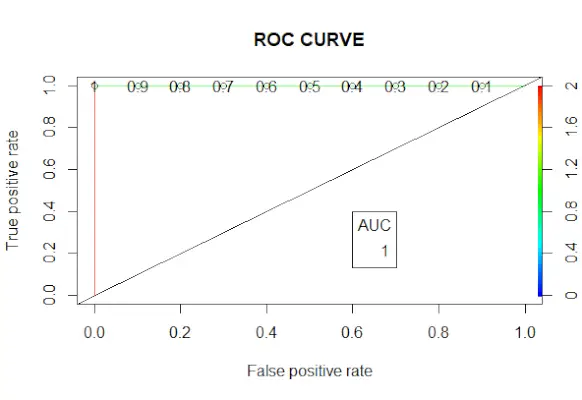
Крива ROC
приклад 2:
Ми можемо виконати модель логістичної регресії Titanic Data set у R.
Р
# Load the dataset> data> (Titanic)> # Convert the table to a data frame> data <-> as.data.frame> (Titanic)> # Fit the logistic regression model> model <-> glm> (Survived ~ Class + Sex + Age, family = binomial, data = data)> # View the summary of the model> summary> (model)> |
Вихід:
Call: glm(formula = Survived ~ Class + Sex + Age, family = binomial, data = data) Deviance Residuals: Min 1Q Median 3Q Max -1.177 -1.177 0.000 1.177 1.177 Coefficients: Estimate Std. Error z value Pr(>|z|) (Перехоплення) 4.022e-16 8.660e-01 0 1 Class2nd -9.762e-16 1.000e+00 0 1 Class3rd -4.699e-16 1.000e+00 0 1 ClassCrew -5.551e-16 1.000e+ 00 0 1 SexFemale -3.140e-16 7.071e-01 0 1 AgeAdult 5.103e-16 7.071e-01 0 1 (параметр дисперсії для біноміальної сім’ї приймається рівним 1) Нульове відхилення: 44,361 на 31 ступені свободи Залишкове відхилення: 44,361 на 26 ступенях свободи AIC: 56,361 Кількість ітерацій оцінки Фішера: 2
Побудуйте криву ROC для набору даних Titanic
Р
# Install and load the required packages> install.packages> (> 'ROCR'> )> library> (ROCR)> # Fit the logistic regression model> model <-> glm> (Survived ~ Class + Sex + Age, family = binomial, data = data)> # Make predictions on the dataset> predictions <-> predict> (model, type => 'response'> )> # Create a prediction object for ROCR> prediction_objects <-> prediction> (predictions, titanic_df$Survived)> # Create an ROC curve object> roc_object <-> performance> (prediction_obj, measure => 'tpr'> , x.measure => 'fpr'> )> # Plot the ROC curve> plot> (roc_object, main => 'ROC Curve'> , col => 'blue'> , lwd = 2)> # Add labels and a legend to the plot> legend> (> 'bottomright'> , legend => > paste> (> 'AUC ='> ,> round> (> performance> (prediction_objects, measure => 'auc'> )> > @y.values[[1]], 2)), col => 'blue'> , lwd = 2)> |
Вихід:
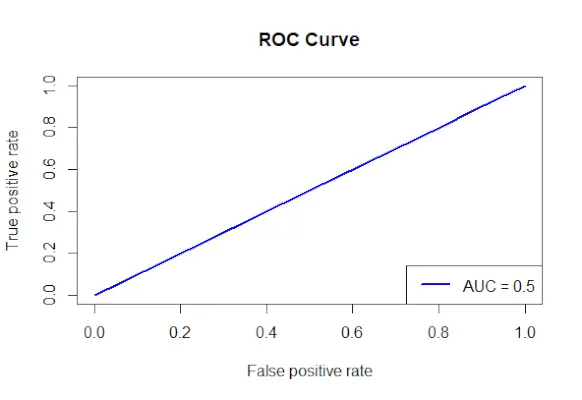
ROC крива
- Фактори, які використовуються для прогнозування вижили, визначені, а формула вижили клас + стать + вік використовується для створення моделі логістичної регресії.
- За допомогою функції predict() прогнози робляться для набору даних за допомогою підігнаної моделі.
- Прогнозовані ймовірності поєднуються з фактичними значеннями результатів для створення об’єкта передбачення за допомогою методу prediction() із пакету ROCR.
- Вказується міра істинної позитивної швидкості (tpr) і міра хибно позитивної швидкості (fpr) по осі X, а об’єкт кривої ROC створюється за допомогою функції performance() із пакета ROCR.
- Об’єкт кривої ROC (roc_obj), який визначає головний заголовок, колір і ширину лінії, будується за допомогою функції plot().
- Він використовує функцію performance() із вимірюванням = auc для визначення значення AUC (площа під кривою) і додає мітки та легенду до графіка.