Цей посібник є посібником для початківців вивчення структур даних і алгоритмів за допомогою Python. У цій статті ми обговоримо вбудовані структури даних, такі як списки, кортежі, словники тощо, а також деякі визначені користувачем структури даних, такі як пов'язані списки , дерева , графіки тощо, а також обхід, а також алгоритми пошуку та сортування за допомогою хороших і добре пояснених прикладів і практичних запитань.

списки

Списки Python це впорядковані набори даних, як і масиви в інших мовах програмування. Він дозволяє різні типи елементів у списку. Реалізація списку Python подібна до Vectors у C++ або ArrayList у JAVA. Дорогою операцією є вставлення або видалення елемента з початку списку, оскільки всі елементи потрібно зсунути. Вставлення та видалення в кінці списку також може бути дорогим у випадку, коли попередньо виділена пам'ять стає повною.

Приклад: створення списку Python

List = [1, 2, 3, 'GFG', 2.3] print(List) 

[1, 2, 3, 'GFG', 2.3] 

До елементів списку можна отримати доступ за призначеним індексом. У Python початковий індекс списку — це 0, а кінцевий індекс — N-1 (якщо є N елементів).

Приклад: операції зі списками Python

# Creating a List with # the use of multiple values List = ['Geeks', 'For', 'Geeks'] print('
List containing multiple values: ') print(List) # Creating a Multi-Dimensional List # (By Nesting a list inside a List) List2 = [['Geeks', 'For'], ['Geeks']] print('
Multi-Dimensional List: ') print(List2) # accessing a element from the # list using index number print('Accessing element from the list') print(List[0]) print(List[2]) # accessing a element using # negative indexing print('Accessing element using negative indexing') # print the last element of list print(List[-1]) # print the third last element of list print(List[-3]) 

List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks 

Кортеж

Кортежі Python схожі на списки, але кортежі схожі незмінний у природі, тобто колись створений, його неможливо змінити. Як і список, кортеж також може містити елементи різних типів.

У Python кортежі створюються шляхом розміщення послідовності значень, розділених «комою» з використанням або без використання дужок для групування послідовності даних.

Примітка: Щоб створити кортеж з одного елемента, у кінці має бути кома. Наприклад, (8,) створить кортеж, що містить 8 як елемент.

Приклад: операції кортежу Python

# Creating a Tuple with # the use of Strings Tuple = ('Geeks', 'For') print('
Tuple with the use of String: ') print(Tuple) # Creating a Tuple with # the use of list list1 = [1, 2, 4, 5, 6] print('
Tuple using List: ') Tuple = tuple(list1) # Accessing element using indexing print('First element of tuple') print(Tuple[0]) # Accessing element from last # negative indexing print('
Last element of tuple') print(Tuple[-1]) print('
Third last element of tuple') print(Tuple[-3]) 

Tuple with the use of String: ('Geeks', 'For') Tuple using List: First element of tuple 1 Last element of tuple 6 Third last element of tuple 4 

встановити

Набір Python це змінна колекція даних, яка не допускає дублювання. Набори в основному використовуються для тестування членства та усунення повторюваних записів. Структура даних, яка використовується в цьому, є хешуванням, популярною технікою для виконання вставки, видалення та обходу в середньому в O(1).

Якщо в одній позиції індексу присутні кілька значень, тоді значення додається до цієї позиції індексу, щоб сформувати зв’язаний список. У CPython Sets реалізовано за допомогою словника з фіктивними змінними, де ключові істоти є членами набору з більшою оптимізацією до часової складності.

Реалізація набору:

Набори з численними операціями на одній HashTable:

Приклад: Python Set Operations

# Creating a Set with # a mixed type of values # (Having numbers and strings) Set = set([1, 2, 'Geeks', 4, 'For', 6, 'Geeks']) print('
Set with the use of Mixed Values') print(Set) # Accessing element using # for loop print('
Elements of set: ') for i in Set: print(i, end =' ') print() # Checking the element # using in keyword print('Geeks' in Set) 

Set with the use of Mixed Values {1, 2, 4, 6, 'For', 'Geeks'} Elements of set: 1 2 4 6 For Geeks True 

Заморожені набори

Заморожені набори у Python — це незмінні об’єкти, які підтримують лише методи й оператори, що створюють результат, не впливаючи на заморожений набір або набори, до яких вони застосовуються. Хоча елементи набору можна змінити в будь-який час, елементи замороженого набору залишаються незмінними після створення.

Приклад: набір Python Frozen

# Same as {'a', 'b','c'} normal_set = set(['a', 'b','c']) print('Normal Set') print(normal_set) # A frozen set frozen_set = frozenset(['e', 'f', 'g']) print('
Frozen Set') print(frozen_set) # Uncommenting below line would cause error as # we are trying to add element to a frozen set # frozen_set.add('h') 

Normal Set {'a', 'b', 'c'} Frozen Set frozenset({'f', 'g', 'e'}) 

Рядок

Рядки Python це незмінний масив байтів, що представляють символи Unicode. Python не має символьного типу даних, окремий символ є просто рядком довжиною 1.

Примітка: Оскільки рядки незмінні, зміна рядка призведе до створення нової копії.

Приклад: операції над рядками Python

String = 'Welcome to GeeksForGeeks' print('Creating String: ') print(String) # Printing First character print('
First character of String is: ') print(String[0]) # Printing Last character print('
Last character of String is: ') print(String[-1]) 

Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s 

Словник

Словник Python це невпорядкована колекція даних, яка зберігає дані у форматі пари ключ:значення. Це як хеш-таблиці в будь-якій іншій мові з часовою складністю O(1). Індексування словника Python здійснюється за допомогою ключів. Це будь-який хешований тип, тобто об’єкт, який ніколи не може змінюватися, як рядки, числа, кортежі тощо. Ми можемо створити словник за допомогою фігурних дужок ({}) або розуміння словника.

Приклад: операції словника Python

# Creating a Dictionary Dict = {'Name': 'Geeks', 1: [1, 2, 3, 4]} print('Creating Dictionary: ') print(Dict) # accessing a element using key print('Accessing a element using key:') print(Dict['Name']) # accessing a element using get() # method print('Accessing a element using get:') print(Dict.get(1)) # creation using Dictionary comprehension myDict = {x: x**2 for x in [1,2,3,4,5]} print(myDict) 

Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25} 

Матриця

Матриця — це двовимірний масив, де кожен елемент має строго однаковий розмір. Для створення матриці ми будемо використовувати Пакет NumPy .

Приклад: Матричні операції Python NumPy

import numpy as np a = np.array([[1,2,3,4],[4,55,1,2], [8,3,20,19],[11,2,22,21]]) m = np.reshape(a,(4, 4)) print(m) # Accessing element print('
Accessing Elements') print(a[1]) print(a[2][0]) # Adding Element m = np.append(m,[[1, 15,13,11]],0) print('
Adding Element') print(m) # Deleting Element m = np.delete(m,[1],0) print('
Deleting Element') print(m) 

Вихід

[[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]] Accessing Elements [ 4 55 1 2] 8 Adding Element [[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] Deleting Element [[ 1 2 3 4]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] 

Масив байтів

Python Bytearray дає змінну послідовність цілих чисел у діапазоні 0 <= x < 256.

Приклад: операції Python Bytearray

# Creating bytearray a = bytearray((12, 8, 25, 2)) print('Creating Bytearray:') print(a) # accessing elements print('
Accessing Elements:', a[1]) # modifying elements a[1] = 3 print('
After Modifying:') print(a) # Appending elements a.append(30) print('
After Adding Elements:') print(a) 

Creating Bytearray: bytearray(b'x0cx08x19x02') Accessing Elements: 8 After Modifying: bytearray(b'x0cx03x19x02') After Adding Elements: bytearray(b'x0cx03x19x02x1e') 

Зв'язаний список

А зв'язаний список це лінійна структура даних, у якій елементи не зберігаються в безперервних місцях пам’яті. Елементи у зв’язаному списку зв’язуються за допомогою вказівників, як показано на зображенні нижче:

Зв’язаний список представлений вказівником на перший вузол зв’язаного списку. Перший вузол називається головкою. Якщо пов’язаний список порожній, тоді значення заголовка дорівнює NULL. Кожен вузол у списку складається щонайменше з двох частин:

• Дані
• Покажчик (або посилання) на наступний вузол

Приклад: визначення пов’язаного списку в Python

# Node class class Node: # Function to initialize the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize # next as null # Linked List class class LinkedList: # Function to initialize the Linked # List object def __init__(self): self.head = None 

Давайте створимо простий зв’язаний список із 3 вузлами.

# A simple Python program to introduce a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3)  '''  Three nodes have been created.  We have references to these three blocks as head,  second and third  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | None | | 2 | None | | 3 | None |  +----+------+ +----+------+ +----+------+  ''' llist.head.next = second; # Link first node with second  '''  Now next of first Node refers to second. So they  both are linked.  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | o-------->| 2 | нуль | | 3 | нуль |  +----+------+ +----+------+ +----+------+ ''' другий.наступний = третій ; # Пов’яжіть другий вузол із третім вузлом ''' Тепер наступний другий вузол посилається на третій. Отже, усі три вузли пов’язані.  llist.head другий третій | | |  | | |  +----+------+ +----+------+ +----+------+ | 1 | о-------->| 2 | о-------->| 3 | нуль |  +----+------+ +----+------+ +----+------+ ''' 

Обхід пов’язаного списку

У попередній програмі ми створили простий зв’язаний список із трьома вузлами. Переглянемо створений список і надрукуємо дані кожного вузла. Для обходу давайте напишемо функцію загального призначення printList(), яка друкує будь-який заданий список.

# A simple Python program for traversal of a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # This function prints contents of linked list # starting from head def printList(self): temp = self.head while (temp): print (temp.data) temp = temp.next # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) llist.head.next = second; # Link first node with second second.next = third; # Link second node with the third node llist.printList() 

1 2 3 

Більше статей у пов’язаному списку

• Вставка пов’язаного списку
• Видалення пов’язаного списку (видалення заданого ключа)
• Видалення пов’язаного списку (видалення ключа в заданій позиції)
• Знайти довжину пов’язаного списку (ітеративний і рекурсивний)
• Пошук елемента в пов’язаному списку (ітеративний і рекурсивний)
• N-й вузол з кінця пов’язаного списку
• Перевернути пов’язаний список

А стек це лінійна структура даних, яка зберігає елементи за принципом 'останній прийшов/перший вийшов' (LIFO) або 'перший прийшов/останній вийшов' (FILO). У стеку новий елемент додається на одному кінці, а елемент видаляється лише з цього кінця. Операції вставки та видалення часто називають push і pop.

stack = [] # append() function to push # element in the stack stack.append('g') stack.append('f') stack.append('g') print('Initial stack') print(stack) # pop() function to pop # element from stack in # LIFO order print('
Elements popped from stack:') print(stack.pop()) print(stack.pop()) print(stack.pop()) print('
Stack after elements are popped:') print(stack) # uncommenting print(stack.pop()) # will cause an IndexError # as the stack is now empty 

Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: [] 

Як стек, черга це лінійна структура даних, яка зберігає елементи в порядку FIFO (First In First Out). У черзі спочатку видаляється останній нещодавно доданий елемент. Хорошим прикладом черги є будь-яка черга споживачів для ресурсу, де споживач, який прийшов першим, обслуговується першим.

# Initializing a queue queue = [] # Adding elements to the queue queue.append('g') queue.append('f') queue.append('g') print('Initial queue') print(queue) # Removing elements from the queue print('
Elements dequeued from queue') print(queue.pop(0)) print(queue.pop(0)) print(queue.pop(0)) print('
Queue after removing elements') print(queue) # Uncommenting print(queue.pop(0)) # will raise and IndexError # as the queue is now empty 

Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements [] 

Пріоритетні черги це абстрактні структури даних, у яких кожне дані/значення в черзі мають певний пріоритет. Наприклад, в авіакомпаніях багаж із назвою Business або First-class прибуває раніше за інших. Пріоритетна черга — це розширення черги з такими властивостями.

• Елемент з високим пріоритетом вилучається з черги перед елементом з низьким пріоритетом.
• Якщо два елементи мають однаковий пріоритет, вони обслуговуються відповідно до свого порядку в черзі.

# A simple implementation of Priority Queue # using Queue. class PriorityQueue(object): def __init__(self): self.queue = [] def __str__(self): return ' '.join([str(i) for i in self.queue]) # for checking if the queue is empty def isEmpty(self): return len(self.queue) == 0 # for inserting an element in the queue def insert(self, data): self.queue.append(data) # for popping an element based on Priority def delete(self): try: max = 0 for i in range(len(self.queue)): if self.queue[i]>self.queue[max]: max = i item = self.queue[max] del self.queue[max] повертає елемент крім IndexError: print() exit() if __name__ == '__main__': myQueue = PriorityQueue( ) myQueue.insert(12) myQueue.insert(1) myQueue.insert(14) myQueue.insert(7) print(myQueue) без myQueue.isEmpty(): print(myQueue.delete()) 

12 1 14 7 14 12 7 1 

Купа

модуль heapq у Python забезпечує структуру даних купи, яка в основному використовується для представлення пріоритетної черги. Властивість цієї структури даних полягає в тому, що вона завжди дає найменший елемент (мінімальна купа), коли елемент витягується. Кожного разу, коли елементи штовхаються або висуваються, структура купи зберігається. Елемент heap[0] також кожного разу повертає найменший елемент. Він підтримує витяг і вставку найменшого елемента в O(log n) разів.

Загалом купи можуть бути двох типів:

• Максимальна купа: У Max-Heap ключ, присутній у кореневому вузлі, має бути найбільшим серед ключів, присутніх у всіх дочірніх вузлах. Та сама властивість має бути рекурсивно істинною для всіх піддерев у цьому бінарному дереві.
• Мінімальна купа: У Min-Heap ключ, присутній у кореневому вузлі, має бути мінімальним серед ключів, присутніх у всіх дочірніх вузлах. Та сама властивість має бути рекурсивно істинною для всіх піддерев у цьому бінарному дереві.

# importing 'heapq' to implement heap queue import heapq # initializing list li = [5, 7, 9, 1, 3] # using heapify to convert list into heap heapq.heapify(li) # printing created heap print ('The created heap is : ',end='') print (list(li)) # using heappush() to push elements into heap # pushes 4 heapq.heappush(li,4) # printing modified heap print ('The modified heap after push is : ',end='') print (list(li)) # using heappop() to pop smallest element print ('The popped and smallest element is : ',end='') print (heapq.heappop(li)) 

The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1 

Більше статей про Heap

• Бінарна купа
• K’-й найбільший елемент у масиві
• K’-й найменший/найбільший елемент у несортованому масиві
• Сортувати майже відсортований масив
• K-й найбільший суміжний підмасив
• Мінімальна сума двох чисел, утворених із цифр масиву

Дерево — це ієрархічна структура даних, яка виглядає так, як показано на малюнку нижче:

 tree  ----  j  <-- root  /   f k  /   a h z  <-- leaves 

Найвищий вузол дерева називається коренем, тоді як найнижчі вузли або вузли без дітей називаються листовими вузлами. Вузли, які знаходяться безпосередньо під вузлом, називаються його дочірніми, а вузли, які знаходяться безпосередньо над чимось, називаються його батьківськими.

А бінарне дерево це дерево, елементи якого можуть мати майже двох дітей. Оскільки кожен елемент у бінарному дереві може мати лише 2 дочірні елементи, ми зазвичай називаємо їх лівими та правими дочірніми елементами. Вузол двійкового дерева містить такі частини.

• Дані
• Покажчик на ліву дитину
• Вказівник на праву дитину

Приклад: визначення класу вузла

# A Python class that represents an individual node # in a Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key 

Тепер давайте створимо дерево з 4 вузлами на Python. Припустімо, що структура дерева виглядає так:

 tree  ----  1  <-- root  /   2 3   /  4 

Приклад: додавання даних до дерева

# Python program to introduce Binary Tree # A class that represents an individual node in a # Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key # create root root = Node(1) ''' following is the tree after above statement  1  /   None None''' root.left = Node(2); root.right = Node(3); ''' 2 and 3 become left and right children of 1  1  /   2 3  /  /  None None None None''' root.left.left = Node(4); '''4 becomes left child of 2  1  /   2 3  /  /  4 None None None /  None None''' 

Обхід дерева

Дерева можна обійти різними способами. Нижче наведені способи, які зазвичай використовуються для обходу дерев. Давайте розглянемо дерево нижче –

 tree  ----  1  <-- root  /   2 3   /  4 5 

Перші обходи глибини:

• У порядку (ліворуч, корінь, праворуч): 4 2 5 1 3
• Попереднє замовлення (Root, Left, Right): 1 2 4 5 3
• Постпорядок (ліворуч, праворуч, корінь): 4 5 2 3 1

Алгоритм у порядку (дерево)

• Перейти до лівого піддерева, тобто викликати Inorder(left-subtree)
• Відвідайте корінь.
• Перейти до правого піддерева, тобто викликати Inorder(right-subtree)

Попереднє замовлення алгоритму (дерево)

• Відвідайте корінь.
• Перейти до лівого піддерева, тобто викликати Preorder(left-subtree)
• Перейти до правого піддерева, тобто викликати Preorder(right-subtree)

Алгоритм Поштовий переказ (дерево)

• Перейти до лівого піддерева, тобто викликати Postorder(left-subtree)
• Перейти до правого піддерева, тобто викликати Postorder(right-subtree)
• Відвідайте корінь.

# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do inorder tree traversal def printInorder(root): if root: # First recur on left child printInorder(root.left) # then print the data of node print(root.val), # now recur on right child printInorder(root.right) # A function to do postorder tree traversal def printPostorder(root): if root: # First recur on left child printPostorder(root.left) # the recur on right child printPostorder(root.right) # now print the data of node print(root.val), # A function to do preorder tree traversal def printPreorder(root): if root: # First print the data of node print(root.val), # Then recur on left child printPreorder(root.left) # Finally recur on right child printPreorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Preorder traversal of binary tree is') printPreorder(root) print('
Inorder traversal of binary tree is') printInorder(root) print('
Postorder traversal of binary tree is') printPostorder(root) 

Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1 

Часова складність – O(n)

Обхід порядку в ширину або рівня

Обхід порядку рівня дерева — це обхід дерева в ширину. Порядок обходу рівня вищевказаного дерева 1 2 3 4 5.

Для кожного вузла спочатку відвідується вузол, а потім його дочірні вузли поміщаються в чергу FIFO. Нижче наведено алгоритм для того ж –

• Створіть порожню чергу q
• temp_node = root /*почати з кореня*/
• Цикл, поки temp_node не NULL
  • надрукувати temp_node->data.
  • Поставте в чергу дочірніх елементів temp_node (спочатку лівих, а потім правих) до q
  • Виключити вузол із q

# Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self ,key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Надрукувати початок черги та # видалити його з черги print (queue[0].data) node = queue.pop(0) # Поставити в чергу лівого дочірнього елемента, якщо node.left не є None: queue.append(node.left) ) # Поставити в чергу правий дочірній елемент, якщо node.right не є None: queue.append(node.right) # Програма драйвера для тестування вищевказаної функції root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print ('Обхід рівня порядку бінарного дерева є -') printLevelOrder(root) 

Level Order Traversal of binary tree is - 1 2 3 4 5 

Часова складність: O(n)

Більше статей про бінарне дерево

• Вставка в бінарне дерево
• Видалення в бінарному дереві
• Упорядкований обхід дерева без рекурсії
• Inorder Tree Traversal без рекурсії та без стека!
• Роздрукувати обхід після замовлення з заданих обходів у порядку та попереднього замовлення
• Знайти обхід після замовлення BST з обходу попереднього замовлення

Двійкове дерево пошуку це структура даних бінарного дерева на основі вузлів, яка має такі властивості:

# A utility function to search a given key in BST def search(root,key): # Base Cases: root is null or key is present at root if root is None or root.val == key: return root # Key is greater than root's key if root.val  < key: return search(root.right,key) # Key is smaller than root's key return search(root.left,key) 

# Python program to demonstrate # insert operation in binary search tree # A utility class that represents # an individual node in a BST class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A utility function to insert # a new node with the given key def insert(root, key): if root is None: return Node(key) else: if root.val == key: return root elif root.val  < key: root.right = insert(root.right, key) else: root.left = insert(root.left, key) return root # A utility function to do inorder tree traversal def inorder(root): if root: inorder(root.left) print(root.val) inorder(root.right) # Driver program to test the above functions # Let us create the following BST # 50 # /  # 30 70 # /  /  # 20 40 60 80 r = Node(50) r = insert(r, 30) r = insert(r, 20) r = insert(r, 40) r = insert(r, 70) r = insert(r, 60) r = insert(r, 80) # Print inorder traversal of the BST inorder(r) 

20 30 40 50 60 70 80 

А графік це нелінійна структура даних, що складається з вузлів і ребер. Вузли іноді також називають вершинами, а ребра — лініями або дугами, які з’єднують будь-які два вузли в графі. Більш формально граф можна визначити як граф, що складається зі скінченного набору вершин (або вузлів) і набору ребер, які з’єднують пару вузлів.

# A simple representation of graph using Adjacency Matrix class Graph: def __init__(self,numvertex): self.adjMatrix = [[-1]*numvertex for x in range(numvertex)] self.numvertex = numvertex self.vertices = {} self.verticeslist =[0]*numvertex def set_vertex(self,vtx,id): if 0 <=vtx <=self.numvertex: self.vertices[id] = vtx self.verticeslist[vtx] = id def set_edge(self,frm,to,cost=0): frm = self.vertices[frm] to = self.vertices[to] self.adjMatrix[frm][to] = cost # for directed graph do not add this self.adjMatrix[to][frm] = cost def get_vertex(self): return self.verticeslist def get_edges(self): edges=[] for i in range (self.numvertex): for j in range (self.numvertex): if (self.adjMatrix[i][j]!=-1): edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j])) return edges def get_matrix(self): return self.adjMatrix G =Graph(6) G.set_vertex(0,'a') G.set_vertex(1,'b') G.set_vertex(2,'c') G.set_vertex(3,'d') G.set_vertex(4,'e') G.set_vertex(5,'f') G.set_edge('a','e',10) G.set_edge('a','c',20) G.set_edge('c','b',30) G.set_edge('b','e',40) G.set_edge('e','d',50) G.set_edge('f','e',60) print('Vertices of Graph') print(G.get_vertex()) print('Edges of Graph') print(G.get_edges()) print('Adjacency Matrix of Graph') print(G.get_matrix()) 

# A class to represent the adjacency list of the node class AdjNode: def __init__(self, data): self.vertex = data self.next = None # A class to represent a graph. A graph # is the list of the adjacency lists. # Size of the array will be the no. of the # vertices 'V' class Graph: def __init__(self, vertices): self.V = vertices self.graph = [None] * self.V # Function to add an edge in an undirected graph def add_edge(self, src, dest): # Adding the node to the source node node = AdjNode(dest) node.next = self.graph[src] self.graph[src] = node # Adding the source node to the destination as # it is the undirected graph node = AdjNode(src) node.next = self.graph[dest] self.graph[dest] = node # Function to print the graph def print_graph(self): for i in range(self.V): print('Adjacency list of vertex {}
 head'.format(i), end='') temp = self.graph[i] while temp: print(' ->{}'.format(temp.vertex), end='') temp = temp.next print(' 
') # Програма-драйвер для вищевказаного класу графа, якщо __name__ == '__main__' : V = 5 graph = Graph(V) graph.add_edge(0, 1) graph.add_edge(0, 4) graph.add_edge(1, 2) graph.add_edge(1, 3) graph.add_edge(1, 4) graph.add_edge(2, 3) graph.add_edge(3, 4) graph.print_graph() 

Adjacency list of vertex 0 head ->4 -> 1 Список суміжності голови вершини 1 -> 4 -> 3 -> 2 -> 0 Список суміжності голови вершини 2 -> 3 -> 1 Список суміжності голови вершини 3 -> 4 -> 2 -> 1 Суміжність список головок вершини 4 -> 3 -> 1 -> 0>>   
 Обхід графа  
 
 Пошук у ширину або BFS  
  
     Обхід у ширину    для графа схоже на обхід дерева в ширину. Єдина заковика тут полягає в тому, що на відміну від дерев, графи можуть містити цикли, тож ми можемо знову прийти до того самого вузла. Щоб уникнути обробки вузла більше одного разу, ми використовуємо булевий відвіданий масив. Для простоти передбачається, що всі вершини досяжні з початкової вершини.  
  
 Наприклад, у наступному графі ми починаємо обхід з вершини 2. Коли ми приходимо до вершини 0, ми шукаємо всі суміжні з нею вершини. 2 також є суміжною вершиною 0. Якщо ми не позначаємо відвідані вершини, тоді 2 буде оброблено знову, і це стане незавершеним процесом. Обхід у ширину наступного графіка дорівнює 2, 0, 3, 1.  
  
     
Python3   
# Python3 Program to print BFS traversal # from a given source vertex. BFS(int s) # traverses vertices reachable from s. from collections import defaultdict # This class represents a directed graph # using adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self,u,v): self.graph[u].append(v) # Function to print a BFS of graph def BFS(self, s): # Mark all the vertices as not visited visited = [False] * (max(self.graph) + 1) # Create a queue for BFS queue = [] # Mark the source node as # visited and enqueue it queue.append(s) visited[s] = True while queue: # Dequeue a vertex from # queue and print it s = queue.pop(0) print (s, end = ' ') # Get all adjacent vertices of the # dequeued vertex s. If a adjacent # has not been visited, then mark it # visited and enqueue it for i in self.graph[s]: if visited[i] == False: queue.append(i) visited[i] = True # Driver code # Create a graph given in # the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print ('Following is Breadth First Traversal' ' (starting from vertex 2)') g.BFS(2) 
    
  Вихід    Часова складність: O(V+E), де V — кількість вершин у графі, а E — кількість ребер у графі.  
  
 Пошук за глибиною або DFS  
 
   Перший обхід глибини    для графіка схоже на обхід дерева за глибиною. Єдина заковика тут полягає в тому, що на відміну від дерев, графи можуть містити цикли, вузол можна відвідати двічі. Щоб уникнути обробки вузла більше одного разу, використовуйте булевий відвіданий масив.  
  
    Алгоритм:     
  
 
 Створіть рекурсивну функцію, яка приймає індекс вузла та відвіданого масиву.  
 
 Позначте поточний вузол як відвіданий і надрукуйте вузол.  
 
 Перейдіть по всіх суміжних і непозначених вузлах і викличте рекурсивну функцію з індексом сусіднього вузла.  
 
Python3   
# Python3 program to print DFS traversal # from a given graph from collections import defaultdict # This class represents a directed graph using # adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self, u, v): self.graph[u].append(v) # A function used by DFS def DFSUtil(self, v, visited): # Mark the current node as visited # and print it visited.add(v) print(v, end=' ') # Recur for all the vertices # adjacent to this vertex for neighbour in self.graph[v]: if neighbour not in visited: self.DFSUtil(neighbour, visited) # The function to do DFS traversal. It uses # recursive DFSUtil() def DFS(self, v): # Create a set to store visited vertices visited = set() # Call the recursive helper function # to print DFS traversal self.DFSUtil(v, visited) # Driver code # Create a graph given # in the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print('Following is DFS from (starting from vertex 2)') g.DFS(2) 
    
  Вихід   
Following is DFS from (starting from vertex 2) 2 0 1 3 
  
 Більше статей про граф  
 
 
  Графічне представлення за допомогою набору та хешу   
 
  Знайдіть материнську вершину на графі   
 
  Ітеративний пошук глибини   
 
  Підрахуйте кількість вузлів на заданому рівні в дереві за допомогою BFS   
 
  Порахувати всі можливі шляхи між двома вершинами   
 
 
  Процес, у якому функція викликає саму себе прямо чи опосередковано, називається рекурсією, а відповідна функція називається a    рекурсивна функція   . Використовуючи рекурсивні алгоритми, певні проблеми можна вирішити досить легко. Прикладами таких проблем є Ханойські вежі (TOH), обхід дерев у порядку/попередньому порядку/постпорядку, DFS графа тощо.   
   
 Що таке базова умова в рекурсії?  
 
 У рекурсивній програмі надається розв’язок базового випадку, а розв’язок більшої проблеми виражається через менші проблеми.  
  
def fact(n):  # base case  if (n  <= 1)   return 1  else   return n*fact(n-1) 
 
 У наведеному вище прикладі визначено базовий варіант для n  <= 1, і більше значення числа можна розв’язати шляхом перетворення на менше, доки не буде досягнуто базового випадку.  
  
 Як пам'ять розподіляється для викликів різних функцій у рекурсії?  
 
 Коли будь-яка функція викликається з main(), їй виділяється пам'ять у стеку. Рекурсивна функція викликає сама себе, пам’ять для викликаної функції виділяється поверх пам’яті, виділеної для функції, що викликає, і для кожного виклику функції створюється інша копія локальних змінних. Коли базовий варіант досягнуто, функція повертає своє значення функції, якою вона була викликана, пам’ять звільняється, і процес продовжується.  
  
 Розглянемо приклад роботи рекурсії, взявши просту функцію.  
Python3   
# A Python 3 program to # demonstrate working of # recursion def printFun(test): if (test  < 1): return else: print(test, end=' ') printFun(test-1) # statement 2 print(test, end=' ') return # Driver Code test = 3 printFun(test) 
    
  Вихід   
3 2 1 1 2 3 
  
 Стек пам'яті показано на схемі нижче.  
  
  
  
 Більше статей про рекурсію  
  
  
  Рекурсія   
  
     Рекурсія в Python    
 
  Практичні запитання для рекурсії | Набір 1   
 
  Практичні запитання для рекурсії | Набір 2   
 
  Практичні запитання для рекурсії | Набір 3   
 
  Практичні запитання для рекурсії | Набір 4   
 
  Практичні запитання для рекурсії | Набір 5   
 
  Практичні запитання для рекурсії | Набір 6   
 
  Практичні запитання для рекурсії | Набір 7   
 
 
     >>> Більше      
  
    Динамічне програмування     
 
   Динамічне програмування    це в основному оптимізація над простою рекурсією. Усюди, де ми бачимо рекурсивне рішення, яке повторює виклики для тих самих вхідних даних, ми можемо оптимізувати його за допомогою динамічного програмування. Ідея полягає в тому, щоб просто зберігати результати підпроблем, щоб нам не довелося повторно обчислювати їх, коли це буде потрібно пізніше. Ця проста оптимізація зменшує часові складності від експоненціальної до поліноміальної. Наприклад, якщо ми пишемо просте рекурсивне рішення для чисел Фібоначчі, ми отримуємо експоненціальну часову складність, і якщо ми оптимізуємо його, зберігаючи рішення підпроблем, часова складність зменшується до лінійної.  
  
  
  
 Табуляція проти мемоізації  
 
 Є два різні способи зберігання значень, щоб значення підпроблеми можна було використовувати повторно. Тут ми обговоримо два шаблони вирішення проблеми динамічного програмування (DP):  
  
 
    Таблиця:     Знизу вгору  
 
    Запам'ятовування:     З верху до низу  
 
 
 Табулювання  
 
 Як випливає з назви, починайте знизу та накопичуйте відповіді до верху. Давайте обговоримо з точки зору переходу стану.  
  
 Давайте опишемо стан нашої проблеми DP як dp[x] з dp[0] як базовим станом і dp[n] як нашим станом призначення. Отже, нам потрібно знайти значення стану призначення, тобто dp[n].  
  
 Якщо ми починаємо наш перехід із нашого базового стану, тобто dp[0], і дотримуємося зв’язку переходу стану, щоб досягти кінцевого стану dp[n], ми називаємо це підходом «знизу вгору», оскільки цілком зрозуміло, що ми почали наш перехід із нижнього базового стану та досягли найвищого бажаного стану.  
  
 Чому ми називаємо це методом таблиць?  
  
 Щоб дізнатися це, давайте спочатку напишемо код для обчислення факторіала числа за допомогою підходу «знизу вгору». Ще раз, як наша загальна процедура вирішення DP, ми спочатку визначаємо стан. У цьому випадку ми визначаємо стан як dp[x], де dp[x] потрібно знайти факторіал x.  
  
 Тепер цілком очевидно, що dp[x+1] = dp[x] * (x+1)  
  
# Tabulated version to find factorial x. dp = [0]*MAXN # base case dp[0] = 1; for i in range(n+1):  dp[i] = dp[i-1] * i 
 
 Запам'ятовування  
 
 Ще раз опишемо це в термінах переходу стану. Якщо нам потрібно знайти значення для якогось стану, скажімо dp[n], і замість того, щоб починати з базового стану, тобто dp[0], ми запитуємо нашу відповідь у станів, які можуть досягти стану призначення dp[n] після переходу стану відношення, то це мода DP зверху вниз.  
  
 Тут ми починаємо нашу подорож із самого верхнього стану призначення та обчислюємо його відповідь, беручи до уваги значення станів, які можуть досягти стану призначення, доки не досягнемо найнижчого базового стану.  
  
 Давайте ще раз напишемо код для факторіальної задачі в режимі зверху вниз  
  
# Memoized version to find factorial x. # To speed up we store the values # of calculated states # initialized to -1 dp[0]*MAXN # return fact x! def solve(x):  if (x==0)  return 1  if (dp[x]!=-1)  return dp[x]  return (dp[x] = x * solve(x-1)) 
 
  
  
 Більше статей про динамічне програмування  
 
 
  Оптимальна властивість субструктури   
 
  Властивість підпроблем, що перекриваються   
 
   Числа Фібоначчі    
 
  Підмножина із сумою, що ділиться на m   
 
  Підпослідовність із збільшенням максимальної суми   
 
  Найдовший загальний підрядок   
 
 
      >>> Більше       
  
 Алгоритми пошуку  
 
 Лінійний пошук  
 
 
 Почніть з крайнього лівого елемента arr[] і один за одним порівняйте x з кожним елементом arr[]  
 
 Якщо x збігається з елементом, поверніть індекс.  
 
 Якщо x не збігається з жодним із елементів, поверніть -1.  
 
  
     
Python3   
# Python3 code to linearly search x in arr[]. # If x is present then return its location, # otherwise return -1 def search(arr, n, x): for i in range(0, n): if (arr[i] == x): return i return -1 # Driver Code arr = [2, 3, 4, 10, 40] x = 10 n = len(arr) # Function call result = search(arr, n, x) if(result == -1): print('Element is not present in array') else: print('Element is present at index', result) 
    
  Вихід   
Element is present at index 3 
  
 Часова складність наведеного вище алгоритму становить O(n).  
  
 Для отримання додаткової інформації див   Лінійний пошук   .  
  
 Двійковий пошук  
 
 Пошук у відсортованому масиві, кілька разів поділяючи інтервал пошуку навпіл. Почніть з інтервалу, що охоплює весь масив. Якщо значення ключа пошуку менше, ніж елемент у середині інтервалу, звузіть інтервал до нижньої половини. В іншому випадку звузіть його до верхньої половини. Повторно перевіряйте, доки значення не буде знайдено або інтервал не буде порожнім.  
  
     
Python3   
# Python3 Program for recursive binary search. # Returns index of x in arr if present, else -1 def binarySearch (arr, l, r, x): # Check base case if r>= l: mid = l + (r - l) // 2 # Якщо елемент присутній у самій середині if arr[mid] == x: return mid # Якщо елемент менший за mid, то він # може бути присутнім лише у лівому підмасиві elif arr[mid]> x: повертає binarySearch(arr, l, mid-1, x) # Інакше елемент може бути присутнім лише # у правому підмасиві else: повертає binarySearch(arr, mid + 1, r, x ) else: # Елемент відсутній в масиві return -1 # Код драйвера arr = [ 2, 3, 4, 10, 40 ] x = 10 # Результат виклику функції = binarySearch(arr, 0, len(arr)-1 , x) if result != -1: print ('Елемент присутній в індексі % d' % результат) else: print ('Елемент відсутній в масиві') 
    
  Вихід   
Element is present at index 3 
  
 Часова складність наведеного вище алгоритму становить O(log(n)).  
  
 Для отримання додаткової інформації див    Двійковий пошук    .  
  
 Алгоритми сортування  
 
 Сортування вибору  
 
 The    сортування вибору    Алгоритм сортує масив, багаторазово знаходячи мінімальний елемент (з огляду на зростання) з невідсортованої частини та ставлячи його на початок. У кожній ітерації сортування вибору мінімальний елемент (у порядку зростання) з невідсортованого підмасиву вибирається та переміщується до відсортованого підмасиву.  
  
 Блок-схема сортування вибору:  
  
     
Python3   
# Python program for implementation of Selection # Sort import sys A = [64, 25, 12, 22, 11] # Traverse through all array elements for i in range(len(A)): # Find the minimum element in remaining # unsorted array min_idx = i for j in range(i+1, len(A)): if A[min_idx]>A[j]: min_idx = j # Поміняти місцями знайдений мінімальний елемент # першим елементом A[i], A[min_idx] = A[min_idx], A[i] # Код драйвера для перевірки над print ('Відсортований масив ') для i в діапазоні (len(A)): print('%d' %A[i]), 
    
  Вихід   
Sorted array 11 12 22 25 64 
  
    Часова складність:     O(n   2   ), оскільки є два вкладені цикли.  
  
    Допоміжний простір:     О(1)  
  
 Бульбашкове сортування  
 
   Бульбашкове сортування    це найпростіший алгоритм сортування, який працює шляхом повторної заміни суміжних елементів, якщо вони розташовані в неправильному порядку.  
  
    Ілюстрація:     
  
     
Python3   
# Python program for implementation of Bubble Sort def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): # Last i elements are already in place for j in range(0, n-i-1): # traverse the array from 0 to n-i-1 # Swap if the element found is greater # than the next element if arr[j]>arr[j+1] : arr[j], arr[j+1] = arr[j+1], arr[j] # Код драйвера для перевірки вище arr = [64, 34, 25, 12, 22, 11 , 90] bubbleSort(arr) print ('Відсортований масив:') для i в діапазоні(len(arr)): print ('%d' %arr[i]), 
    
  Вихід   
Sorted array is: 11 12 22 25 34 64 90 
  
    Часова складність:     O(n   2   )  
  
 Сортування вставкою  
 
 Щоб відсортувати масив розміром n у порядку зростання, використовуйте    сортування вставкою    :  
  
 
 Ітерація від arr[1] до arr[n] по масиву.  
 
 Порівняти поточний елемент (ключ) з його попередником.  
 
 Якщо ключовий елемент менший за свого попередника, порівняйте його з попередніми елементами. Перемістіть більші елементи на одну позицію вгору, щоб звільнити місце для поміняних елементів.  
 
 
    Ілюстрація:     
  
     
Python3   
# Python program for implementation of Insertion Sort # Function to do insertion sort def insertionSort(arr): # Traverse through 1 to len(arr) for i in range(1, len(arr)): key = arr[i] # Move elements of arr[0..i-1], that are # greater than key, to one position ahead # of their current position j = i-1 while j>= 0 і ключ < arr[j] : arr[j + 1] = arr[j] j -= 1 arr[j + 1] = key # Driver code to test above arr = [12, 11, 13, 5, 6] insertionSort(arr) for i in range(len(arr)): print ('% d' % arr[i]) 
    
  Вихід   
 5 6 11 12 13 
  
    Часова складність:     O(n   2   ))  
  
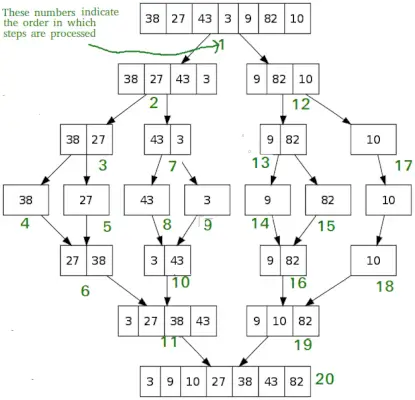
 Сортування злиттям  
 
 Як QuickSort,    Сортування злиттям    це алгоритм розділяй і володарюй. Він ділить вхідний масив на дві половини, викликає себе для двох половин, а потім об’єднує дві відсортовані половини. Функція merge() використовується для злиття двох половинок. Merge(arr, l, m, r) — це ключовий процес, який передбачає, що arr[l..m] і arr[m+1..r] відсортовано, і об’єднує два відсортовані підмасиви в один.  
  
MergeSort(arr[], l, r) If r>l 1. Знайти середню точку, щоб розділити масив на дві половини: середня m = l+ (r-l)/2 2. Викликати mergeSort для першої половини: Викликати mergeSort(arr, l, m) 3. Викликати mergeSort для другої половини: Виклик mergeSort(arr, m+1, r) 4. Об’єднайте дві половини, відсортовані на кроці 2 і 3: Викличте merge(arr, l, m, r) 
  
     
Python3   
# Python program for implementation of MergeSort def mergeSort(arr): if len(arr)>1: # Пошук середини масиву mid = len(arr)//2 # Поділ елементів масиву L = arr[:mid] # на 2 половини R = arr[mid:] # Сортування першої половини mergeSort(L) # Сортування другої половини mergeSort(R) i = j = k = 0 # Копіювання даних до тимчасових масивів L[] і R[], поки i < len(L) and j  < len(R): if L[i]  < R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 # Checking if any element was left while i  < len(L): arr[k] = L[i] i += 1 k += 1 while j  < len(R): arr[k] = R[j] j += 1 k += 1 # Code to print the list def printList(arr): for i in range(len(arr)): print(arr[i], end=' ') print() # Driver Code if __name__ == '__main__': arr = [12, 11, 13, 5, 6, 7] print('Given array is', end='
') printList(arr) mergeSort(arr) print('Sorted array is: ', end='
') printList(arr) 
    
  Вихід   
Given array is 12 11 13 5 6 7 Sorted array is: 5 6 7 11 12 13 
  
    Часова складність:     O(n(logn))  
  
 Швидке сортування  
 
 Як сортування злиттям,    Швидке сортування    це алгоритм розділяй і володарюй. Він вибирає елемент як опору та розбиває заданий масив навколо вибраної опори. Існує багато різних версій QuickSort, які вибирають зведення різними способами.  
  
 Завжди вибирайте перший елемент як опору.  
  
 
 Завжди вибирайте останній елемент як опору (реалізовано нижче)  
 
 Виберіть випадковий елемент як опору.  
 
 Виберіть медіану як опору.  
 
 
 Ключовим процесом у QuickSort є partition(). Ціль розділів полягає в тому, що, враховуючи масив і елемент x масиву як опору, розмістити x у його правильній позиції в сортованому масиві та розмістити всі менші елементи (менші за x) перед x і розмістити всі більші елементи (більші за x) після x. Все це повинно бути зроблено в лінійний час.  
  
/* low -->Початковий індекс, високий --> Кінцевий індекс */ quickSort(arr[], low, high) { if (low { /* pi — індекс поділу, arr[pi] тепер у правильному місці */ pi = partition(arr, low, high); quickSort(arr, low, pi - 1); // Перед pi quickSort(arr, pi + 1, high); // Після pi } 
 
  
  
    Алгоритм розбиття     
  
 Нижче наведено багато способів зробити розділ    псевдокод    приймає метод, наведений у книзі CLRS. Логіка проста, ми починаємо з крайнього лівого елемента і відстежуємо індекс менших (або рівних) елементів як i. Під час обходу, якщо ми знаходимо менший елемент, ми міняємо поточний елемент на arr[i]. В іншому випадку ми ігноруємо поточний елемент.  
  
/* This function takes last element as pivot, places the pivot element at its correct position in sorted array, and places all smaller (smaller than pivot) to left of pivot and all greater elements to right of pivot */ partition (arr[], low, high) {  // pivot (Element to be placed at right position)  pivot = arr[high];   i = (low – 1) // Index of smaller element and indicates the   // right position of pivot found so far  for (j = low; j  <= high- 1; j++){  // If current element is smaller than the pivot  if (arr[j]   i++; // increment index of smaller element  swap arr[i] and arr[j]  }  }  swap arr[i + 1] and arr[high])  return (i + 1) } 
Python3   
# Python3 implementation of QuickSort # This Function handles sorting part of quick sort # start and end points to first and last element of # an array respectively def partition(start, end, array): # Initializing pivot's index to start pivot_index = start pivot = array[pivot_index] # This loop runs till start pointer crosses # end pointer, and when it does we swap the # pivot with element on end pointer while start  < end: # Increment the start pointer till it finds an # element greater than pivot while start  < len(array) and array[start]  <= pivot: start += 1 # Decrement the end pointer till it finds an # element less than pivot while array[end]>pivot: end -= 1 # Якщо початок і кінець не перетинаються, # поміняйте місцями числа на початку і кінці if(start < end): array[start], array[end] = array[end], array[start] # Swap pivot element with element on end pointer. # This puts pivot on its correct sorted place. array[end], array[pivot_index] = array[pivot_index], array[end] # Returning end pointer to divide the array into 2 return end # The main function that implements QuickSort def quick_sort(start, end, array): if (start  < end): # p is partitioning index, array[p] # is at right place p = partition(start, end, array) # Sort elements before partition # and after partition quick_sort(start, p - 1, array) quick_sort(p + 1, end, array) # Driver code array = [ 10, 7, 8, 9, 1, 5 ] quick_sort(0, len(array) - 1, array) print(f'Sorted array: {array}') 
    
  Вихід   
Sorted array: [1, 5, 7, 8, 9, 10] 
  
    Часова складність:     O(n(logn))  
  
 ShellSort  
 
  ShellSort   в основному є різновидом сортування вставкою. При сортуванні вставкою ми переміщуємо елементи лише на одну позицію вперед. Коли елемент потрібно перемістити далеко вперед, потрібно багато рухів. Ідея shellSort полягає в тому, щоб дозволити обмін далекими елементами. У shellSort ми робимо масив h-сортованим за великим значенням h. Ми продовжуємо зменшувати значення h, поки воно не стане 1. Масив називається h-сортованим, якщо всі підсписки кожного h   тис   елемент відсортовано.  
Python3   
# Python3 program for implementation of Shell Sort def shellSort(arr): gap = len(arr) // 2 # initialize the gap while gap>0: i = 0 j = проміжок # перевірити масив зліва направо # до останнього можливого індексу j, поки j < len(arr): if arr[i]>arr[j]: arr[i],arr[j] = arr[j],arr[i] i += 1 j += 1 # тепер ми дивимося назад від i-го індексу ліворуч # міняємо місцями значення, які не в правильному порядку. k = i тоді як k - проміжок> -1: якщо arr[k - проміжок]> arr[k]: arr[k-проміжок],arr[k] = arr[k],arr[k-проміжок] k -= 1 пропуск //= 2 # драйвер для перевірки коду arr2 = [12, 34, 54, 2, 3] print('input array:',arr2) shellSort(arr2) print('sorted array', arr2) 
    
  Вихід   
input array: [12, 34, 54, 2, 3] sorted array [2, 3, 12, 34, 54] 
  
    Часова складність:     O(n   2   ).