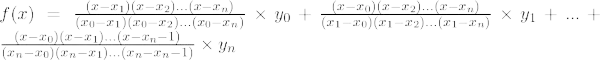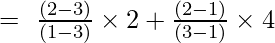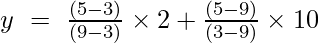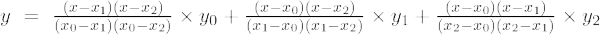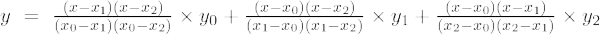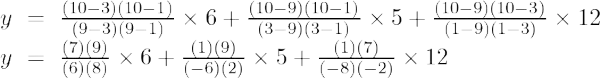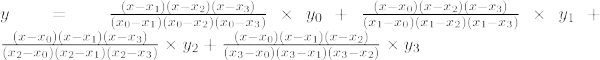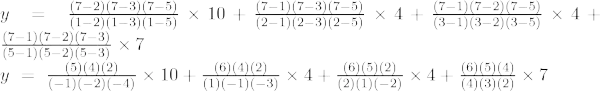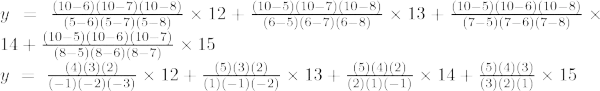ФОРМУЛА ІНТЕРПОЛЯЦІЇ ЛАГРАНЖА: ДОКАЗИ, ПРИКЛАДИ ТА ПОШИРЕНІ ЗАПИТАННЯ

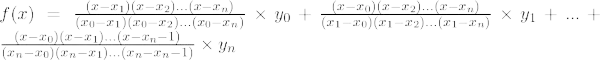
Формула інтерполяції Лагранжа знаходить поліном, званий поліномом Лагранжа, який приймає певні значення в довільній точці. Це n-й ступінь поліноміальний вираз функції f(x). Метод інтерполяції використовується для пошуку нових точок даних у діапазоні дискретного набору відомих точок даних.

У цій статті ми детально дізнаємося про інтерполяцію Лагранжа, формулу інтерполяції Лагранжа, доказ формули інтерполяції Лагранжа, приклади на основі формули інтерполяції Лагранжа та інші.

Що таке інтерполяція Лагранжа?

Інтерполяція Лагранжа — це спосіб знаходження значення будь-якої функції в будь-якій заданій точці, коли функція не задана. Ми використовуємо інші точки функції, щоб отримати значення функції в будь-якій необхідній точці.

Припустимо, що ми маємо функцію y = f(x), у якій заміна значень x дає різні значення y. І нам дають дві точки (х ₁ , і ₁ ) і (x ₂ , і ₂ ) на кривій, тоді значення y при x = a (константа) обчислюється за допомогою формули інтерполяції Лагранжа.

Формула інтерполяції Лагранжа

Дано кілька дійсних значень x ₁ , х ₂ , х ₃ , …, х _п і у ₁ , і ₂ , і ₃ , … і _п і буде поліном P з дійсними коефіцієнтами, що задовольняють умови P(x _i ) = і _i , ∀ i = {1, 2, 3, …, n} і ступінь полінома P має бути меншим за кількість дійсних значень, тобто ступінь (P)

Формула інтерполяції Лагранжа для n-го порядку

Інтерполяційна формула Лагранжа для n ^тис поліном ступеня наведено нижче:

Інтерполяційна формула Лагранжа для n ^тис порядок є,

$f(x)=frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} imes y_0+ frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+...+ frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n$

Інтерполяційна формула Лагранжа першого порядку

Якщо Степінь полінома дорівнює 1, тому його називають поліномом першого порядку. Інтерполяційна формула Лагранжа для 1 ^вул поліноми порядку є,

$f(x)~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1$

Інтерполяційна формула Лагранжа другого порядку

Якщо ступінь полінома дорівнює 2, то він називається поліномом другого порядку. Формула інтерполяції Лагранжа для поліномів 2-го порядку:

$f(x)~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)} {(x_1-x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2$

Доведення теореми Лагранжа

Розглянемо поліном n-го ступеня заданого вигляду,

f(x) = A ₀ (x – x ₁ )(x – x ₂ )(x – x ₃ )…(x – x _п ) + А ₁ (x – x ₁ )(x – x ₂ )(x – x ₃ )…(x – x _п ) + … + А _(n-1) (x – x ₁ )(x – x ₂ )(x – x ₃ )…(x – x _п )

Підставте спостереження x _i отримати А _i

Покладіть x = x ₀ тоді ми отримуємо А ₀

f(x ₀ ) = і ₀ = А ₀ (х ₀ – х ₁ )(x ₀ – х ₂ )(x ₀ – х ₃ )…(x ₀ – х _п )

А ₀ = і ₀ /(x ₀ – х ₁ )(x ₀ – х ₂ )(x ₀ – х ₃ )…(x ₀ – х _п )

Підставляючи x = x ₁ отримуємо А ₁

f(x ₁ ) = і ₁ = А ₁ (х ₁ – х ₀ )(x ₁ – х ₂ )(x ₁ – х ₃ )…(x ₁ – х _п )

А ₁ = і ₁ /(x ₁ – х ₀ )(x ₁ – х ₂ )(x ₁ – х ₃ )…(x ₁ – х _п )

Аналогічно, замінивши x = x _п отримуємо А _п

f(x _п ) = і _п = А _п (х _п – х ₀ )(x _п – х ₁ )(x _п – х ₂ )…(x _п – х _n-1 )

А _п = і _п /(x _п – х ₀ )(x _п – х ₁ )(x _п – х ₂ )…(x _п – х _n-1 )

Якщо підставити всі значення А _i у функції f(x), де i = 1, 2, 3, …n, тоді ми отримуємо формулу інтерполяції Лагранжа як,

$f(x)~=~frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} помножити на y_0+frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)}рази на y_1+... +frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n$

Властивості інтерполяційної формули Лагранжа

Різні властивості формули інтерполяції Лагранжа обговорюються нижче,

Ця формула використовується для знаходження значення функції в будь-якій точці, навіть якщо сама функція не задана.
Він використовується, навіть якщо наведені точки розташовані нерівномірно.
Він дає значення залежної змінної для будь-якої незалежної змінної, що належить до будь-якої функції, і тому використовується в числовому аналізі для знаходження значень функції тощо.

Використання формули інтерполяції Лагранжа

Різні способи використання формули інтерполяції Лагранжа обговорюються нижче,

Він використовується для знаходження значення залежної змінної для будь-якої окремої незалежної змінної, навіть якщо сама функція не задана.
Використовується для масштабування зображення.
Він використовується в моделюванні ШІ.
Використовується для навчання НЛП тощо.

Детальніше,

Формула інтерполяції

Формула лінійної інтерполяції

Приклади використання формули інтерполяції Лагранжа

Давайте розглянемо кілька прикладів запитань щодо формули інтерполяції Лагранжа.

Приклад 1: Знайдіть значення y при x = 2 для заданого набору точок (1, 2), (3, 4)

рішення:

враховуючи,

(х ₀ , і ₀ ) = (1, 2)

(х ₁ , і ₁ ) = (3, 4)

Інтерполяційна формула Лагранжа першого порядку:

$y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1$

При х = 2

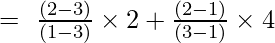
і $=~frac{(2-3)}{(1-3)}рази 2+frac{(2-1)}{(3-1)}рази 4$

y = (-2/-2) + (4/2)

y = 1 + 2 = 3

Значення y при x = 2 дорівнює 3

Приклад 2: Знайдіть значення y при x = 5 для заданого набору точок (9, 2), (3, 10)

рішення:

враховуючи,

(х ₀ , і ₀ ) = (9, 2)

(х ₁ , і ₁ ) = (3, 10)

Інтерполяційна формула Лагранжа першого порядку:

$y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1$

При х = 5

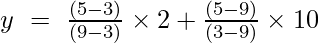
$y~=~frac{(5-3)}{(9-3)} imes 2+frac{(5-9)}{(3-9)} imes 10$

y = (4/6) + (-40/-6)

y = (2/3) + (20/3)

y = 22/3 = 7,33

Значення y при x = 5 дорівнює 7,33

Приклад 3: Знайдіть значення y при x = 1 для заданого набору точок (1, 6), (3, 4), (2, 5)

рішення:

враховуючи,

(х ₀ , і ₀ ) = (1, 6)

(х ₁ , і ₁ ) = (3, 4)

(х ₂ , і ₂ ) = (2, 5)

Формула інтерполяції Лагранжа другого порядку:

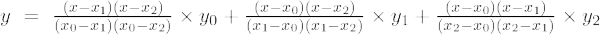
$y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2$

При x = 1

$y~=~frac{(1-3)(1-2)}{(1-3)(1-2)} imes 6+frac{(1-1)(1-2)}{( 3-1)(3-2)} imes 4+frac{(1-1)(1-3)}{(2-1)(2-3)} imes 5 y~=~ frac{(-2)(-1)}{(-2)(-1)} imes 6+frac{(0)(-1)}{(2)(1)} imes 4+frac {(0)(-2)}{(1)(-1)}рази 5$

y = (12/2) + 0 + 0

y = 6

Значення y при x = 1 дорівнює 6

Приклад 4: Знайдіть значення y при x = 10 для заданого набору точок (9, 6), (3, 5), (1, 12)

рішення:

враховуючи,

(х ₀ , і ₀ ) = (9, 6)

(х ₁ , і ₁ ) = (3, 5)

(х ₂ , і ₂ ) = (1, 12)

Формула інтерполяції Лагранжа другого порядку:

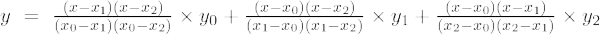
$y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2$

При х = 10

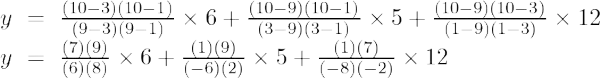
$y~=~frac{(10-3)(10-1)}{(9-3)(9-1)} imes 6+frac{(10-9)(10-1)}{( 3-9)(3-1)} imes 5+frac{(10-9)(10-3)}{(1-9)(1-3)} imes 12 y~=~ frac{(7)(9)}{(6)(8)} imes 6+frac{(1)(9)}{(-6)(2)} imes 5+frac{(1) (7)}{(-8)(-2)}рази 12$

y = (63/8) + (-15/4) + (21/4)

y = (63-30 + 42)/8

y = 75/8 = 9,375

Значення y при x = 10 дорівнює 9,375

Приклад 5: Знайдіть значення y при x = 7 для заданого набору точок (1, 10), (2, 4), (3, 4), (5, 7)

рішення:

враховуючи,

(х ₀ , і ₀ ) = (1, 10)

(х ₁ , і ₁ ) = (2, 4)

(х ₂ , і ₂ ) = (3, 4)

(х ₃ , і ₃ ) = (5, 7)

Інтерполяційна формула Лагранжа третього порядку:

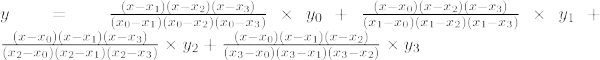
$y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0) )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1) )(x_3-x_2)}рази y_3$

При х = 7

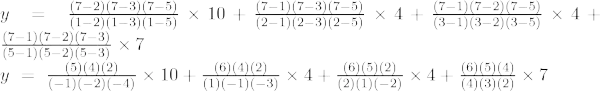
$y~=~frac{(7-2)(7-3)(7-5)}{(1-2)(1-3)(1-5)}рази 10+frac{(7- 1)(7-3)(7-5)}{(2-1)(2-3)(2-5)}рази 4+frac{(7-1)(7-2)(7- 5)}{(3-1)(3-2)(3-5)} imes 4+frac{(7-1)(7-2)(7-3)}{(5-1)( 5-2)(5-3)} imes 7 y~=~frac{(5)(4)(2)}{(-1)(-2)(-4)} imes 10+ frac{(6)(4)(2)}{(1)(-1)(-3)} imes 4+frac{(6)(5)(2)}{(2)(1) (-2)} imes 4+frac{(6)(5)(4)}{(4)(3)(2)} imes 7$

y = -50 + 64 – 60 + 35

y = 99 – 110 = -одинадцять

Значення y при x = 7 дорівнює -11

Приклад 6: Знайдіть значення y при x = 10 для заданого набору точок (5, 12), (6, 13), (7, 14), (8, 15)

рішення:

враховуючи,

(х ₀ , і ₀ ) = (5, 12)

(х ₁ , і ₁ ) = (6, 13)

(х ₂ , і ₂ ) = (7, 14)

(х ₃ , і ₃ ) = (8, 15)

Інтерполяційна формула Лагранжа третього порядку:

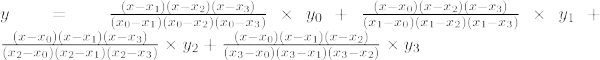
$y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0) )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1) )(x_3-x_2)}рази y_3$

При x = 10,

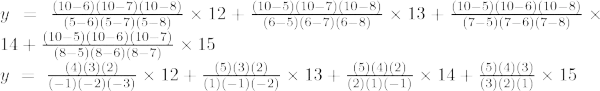
$y~=~frac{(10-6)(10-7)(10-8)}{(5-6)(5-7)(5-8)}разів 12+frac{(10- 5)(10-7)(10-8)}{(6-5)(6-7)(6-8)}разів 13+frac{(10-5)(10-6)(10- 8)}{(7-5)(7-6)(7-8)} imes 14+frac{(10-5)(10-6)(10-7)}{(8-5)( 8-6)(8-7)} imes 15 y~=~frac{(4)(3)(2)}{(-1)(-2)(-3)} imes 12+ frac{(5)(3)(2)}{(1)(-1)(-2)} imes 13+frac{(5)(4)(2)}{(2)(1) (-1)} imes 14+frac{(5)(4)(3)}{(3)(2)(1)} imes 15$

y = -48 + 195 – 280 + 150

y = 17

Значення y при x = 10 дорівнює 17

Приклад 7: Знайдіть значення y при x = 0 для заданого набору точок (-2, 5), (1, 7)

рішення:

враховуючи,

(х ₀ , і ₀ ) = (-2, 5)

(х ₁ , і ₁ ) = (1, 7)

Інтерполяційна формула Лагранжа першого порядку:

$y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1$

При x = 0,

$y~=~frac{(0-1)}{(-2-1)} imes 5+frac{(0+2)}{(1+2)} imes 7$

y = (5/3) + (14/3)

y = 19/3 = 6,33

Значення y при x = 0 дорівнює 6,33

Поширені запитання щодо формули інтерполяції Лагранжа

1. Що таке інтерполяційна формула Лагранжа?

Формула інтерполяції Лагранжа — це формула, яка використовується для знаходження значення залежної змінної функції для будь-якої незалежної змінної, навіть якщо сама функція не задана.

2. Які застосування формули інтерполяції Лагранжа?

Формула Лагранжа має різноманітне застосування в сучасній математиці та науках про дані,

Він використовується для навчання моделі AI.

Він використовується в обробці зображень.

Він використовується для побудови тривимірних та вищих кривих тощо.

3. Що таке інтерполяційна формула Лагранжа першого порядку?

Інтерполяційна формула Лагранжа першого порядку:

f(x) = (x – x ₁ )/(x ₀ – х ₁ )×f ₀ + (x – x ₀ )/(x ₁ – х ₀ )×f ₁

4. Що таке інтерполяційна формула Лагранжа другого порядку?

Інтерполяційна формула Лагранжа другого порядку:

f(x) = [(x – x ₁ )(x – x ₂ )/(x ₀ – х ₁ )(x ₀ – х ₂ )]×f ₀ + [(x – x ₀ )(x – x ₂ )/(x ₁ – х ₀ )(x ₁ – х ₂ )]×f ₁ + [(x – x ₀ )(x – x ₁ )/(x ₂ – х ₀ )(x ₂ – х ₂ )]×f ₀