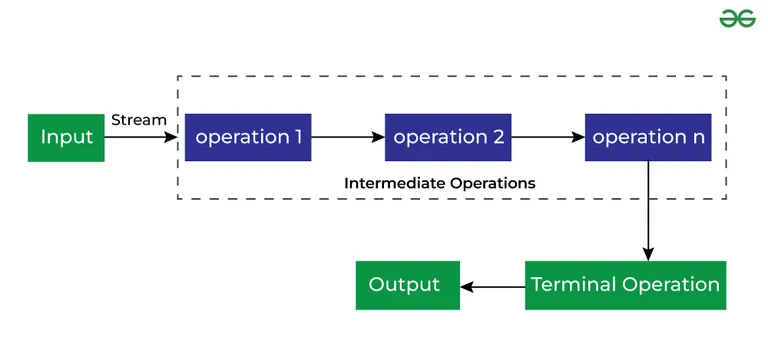
ПОРЯДКОВИЙ ОБХІД БІНАРНОГО ДЕРЕВА - TECHCODEVIEW.COM

Обхід у порядку визначається як вид техніка обходу дерева який відповідає шаблону Ліворуч-Корінь-Право, таким чином:

Першим проходить ліве піддерево

Потім здійснюється обхід кореневого вузла для цього піддерева

Нарешті, обхід правого піддерева здійснюється

Обхід у порядку

Алгоритм обходу бінарного дерева в порядку

Алгоритм обходу в порядку показано таким чином:

Inorder(корінь):

Виконуйте кроки 2-4, доки root не стане != NULL

У порядку (корінь -> ліворуч)

Записати корінь -> дані

У порядку (корінь -> праворуч)

Кінцева петля

Як працює Inorder Traversal бінарного дерева?

Розглянемо таке дерево:

Приклад бінарного дерева

Якщо ми виконуємо обхід у порядку цього бінарного дерева, то обхід буде таким:

Крок 1: Обхід відбуватиметься від 1 до лівого піддерева, тобто 2, потім від 2 до лівого кореня піддерева, тобто 4. Тепер 4 не має лівого піддерева, тому його відвідуватимуть. Він також не має правого піддерева. Отже, більше ніякого обходу з 4

Вузол 4 відвідується

Крок 2: Оскільки ліве піддерево 2 відвідується повністю, тепер він читає дані вузла 2 перед переходом до правого піддерева.

Відвідується вузол 2

крок 3: Тепер буде обхід правого піддерева 2, тобто перехід до вузла 5. Для вузла 5 немає лівого піддерева, тому його відвідують, а після цього обхід повертається, оскільки правого піддерева вузла 5 немає.

Вузол 5 відвідується

крок 4: Оскільки ліве піддерево вузла 1, буде відвідано сам корінь, тобто вузол 1.

Відвідується вузол 1

крок 5: Відвідується ліве піддерево вузла 1 і сам вузол. Отже, тепер буде проходити праве піддерево 1, тобто перейти до вузла 3. Оскільки вузол 3 не має лівого піддерева, його відвідують.

Відвідується вузол 3

Крок 6: Відвідується ліве піддерево вузла 3 і сам вузол. Отже, перейдіть до правого піддерева та відвідайте вузол 6. Тепер обхід завершується, коли пройдено всі вузли.

Проходить повне дерево

Отже, порядок обходу вузлів такий 4 -> 2 -> 5 -> 1 -> 3 -> 6 .

Програма для реалізації Inorder Traversal бінарного дерева:

Нижче наведено реалізацію коду обходу в порядку:

C++

// C++ program for inorder traversals> #include> using> namespace> std;> // Structure of a Binary Tree Node> struct> Node {> > int> data;> > struct> Node *left, *right;> > Node(> int> v)> > {> > data = v;> > left = right = NULL;> > }> };> // Function to print inorder traversal> void> printInorder(> struct> Node* node)> {> > if> (node == NULL)> > return> ;> > // First recur on left subtree> > printInorder(node->ліворуч);> > // Now deal with the node> >

cout ' ';  // Then recur on right subtree  printInorder(node->праворуч); } // Код драйвера int main() { struct Node* root = new Node(1);  root->left = новий вузол (2);  root->right = новий вузол (3);  root->left->left = новий вузол(4);  root->left->right = новий вузол(5);  root->right->right = новий вузол (6);  // Виклик функції cout < < 'Inorder traversal of binary tree is: 
';  printInorder(root);  return 0; }>

Java

// Java program for inorder traversals> import> java.util.*;> // Structure of a Binary Tree Node> class> Node {> > int> data;> > Node left, right;> > Node(> int> v)> > {> > data = v;> > left = right => null> ;> > }> }> // Main class> class> GFG {> > // Function to print inorder traversal> > public> static> void> printInorder(Node node)> > {> > if> (node ==> null> )> > return> ;> > // First recur on left subtree> > printInorder(node.left);> > // Now deal with the node> > System.out.print(node.data +> ' '> );> > // Then recur on right subtree> > printInorder(node.right);> > }> > // Driver code> > public> static> void> main(String[] args)> > {> > Node root => new> Node(> 1> );> > root.left => new> Node(> 2> );> > root.right => new> Node(> 3> );> > root.left.left => new> Node(> 4> );> > root.left.right => new> Node(> 5> );> > root.right.right => new> Node(> 6> );> > // Function call> > System.out.println(> > 'Inorder traversal of binary tree is: '> );> > printInorder(root);> > }> }> // This code is contributed by prasad264>

Python3

# Structure of a Binary Tree Node> class> Node:> > def> __init__(> self> , v):> > self> .data> => v> > self> .left> => None> > self> .right> => None> # Function to print inorder traversal> def> printInorder(node):> > if> node> is> None> :> > return> > # First recur on left subtree> > printInorder(node.left)> > # Now deal with the node> > print> (node.data, end> => ' '> )> > # Then recur on right subtree> > printInorder(node.right)> # Driver code> if> __name__> => => '__main__'> :> > root> => Node(> 1> )> > root.left> => Node(> 2> )> > root.right> => Node(> 3> )> > root.left.left> => Node(> 4> )> > root.left.right> => Node(> 5> )> > root.right.right> => Node(> 6> )> > # Function call> > print> (> 'Inorder traversal of binary tree is:'> )> > printInorder(root)>

C#

// C# program for inorder traversals> using> System;> // Structure of a Binary Tree Node> public> class> Node {> > public> int> data;> > public> Node left, right;> > public> Node(> int> v)> > {> > data = v;> > left = right => null> ;> > }> }> // Class to store and print inorder traversal> public> class> BinaryTree {> > // Function to print inorder traversal> > public> static> void> printInorder(Node node)> > {> > if> (node ==> null> )> > return> ;> > // First recur on left subtree> > printInorder(node.left);> > // Now deal with the node> > Console.Write(node.data +> ' '> );> > // Then recur on right subtree> > printInorder(node.right);> > }> > // Driver code> > public> static> void> Main()> > {> > Node root => new> Node(1);> > root.left => new> Node(2);> > root.right => new> Node(3);> > root.left.left => new> Node(4);> > root.left.right => new> Node(5);> > root.right.right => new> Node(6);> > // Function call> > Console.WriteLine(> > 'Inorder traversal of binary tree is: '> );> > printInorder(root);> > }> }>

Javascript

// JavaScript program for inorder traversals> // Structure of a Binary Tree Node> class Node {> > constructor(v) {> > this> .data = v;> > this> .left => null> ;> > this> .right => null> ;> > }> }> // Function to print inorder traversal> function> printInorder(node) {> > if> (node ===> null> ) {> > return> ;> > }> > > // First recur on left subtree> > printInorder(node.left);> > > // Now deal with the node> > console.log(node.data);> > > // Then recur on right subtree> > printInorder(node.right);> }> // Driver code> const root => new> Node(1);> root.left => new> Node(2);> root.right => new> Node(3);> root.left.left => new> Node(4);> root.left.right => new> Node(5);> root.right.right => new> Node(6);> // Function call> console.log(> 'Inorder traversal of binary tree is: '> );> printInorder(root);>

Вихід

Inorder traversal of binary tree is: 4 2 5 1 3 6

Пояснення:

Як працює обхід у порядку

Аналіз складності:

Часова складність: O(N), де N - загальна кількість вузлів. Тому що він проходить усі вузли принаймні один раз.
Допоміжний простір: O(1), якщо простір стеку рекурсії не розглядається. В іншому випадку O(h), де h — висота дерева

У гіршому випадку ч може бути таким же, як Н (коли дерево перекошене)
У кращому випадку ч може бути таким же, як спокійний (коли дерево є повним деревом)

Випадки використання Inorder Traversal:

У випадку BST (двійкового дерева пошуку), якщо будь-коли виникає потреба отримати вузли в порядку неубування, найкращим способом є реалізація обходу в порядку.

Пов'язані статті: