Вихід:
11 23 4.46 4.48 4.47
Круглі числа в Python u співати Усічення концепція
У цій функції кожна цифра після заданої позиції замінюється на 0. python truncate() функція можна використовувати як з позитивними, так і з негативними числами. Функцію скорочення можна реалізувати таким чином:
- Множення числа на 10^p (10 піднесено до p тис ступінь), щоб зсунути десяткову кому на p знаків праворуч.
- Отримання цілої частини цього нового числа за допомогою int().
- Зрушення десяткового знака p повертається вліво шляхом ділення на 10^p.
python3
# defining truncate function> # second argument defaults to 0> # so that if no argument is passed> # it returns the integer part of number> def> truncate(n, decimals> => 0> ):> > multiplier> => 10> *> *> decimals> > return> int> (n> *> multiplier)> /> multiplier> print> (truncate(> 16.5> ))> print> (truncate(> -> 3.853> ,> 1> ))> print> (truncate(> 3.815> ,> 2> ))> # we can truncate digits towards the left of the decimal point> # by passing a negative number.> print> (truncate(> 346.8> ,> -> 1> ))> print> (truncate(> -> 2947.48> ,> -> 3> ))> |
Вихід:
16.0 -3.8 3.81 340.0 -2000.0
Круглі числа в Python u співати Math.ceil() і Math.floor() функції
математика . стеля() : Ця функція повертає найближче ціле число, яке більше або дорівнює заданому числу.
Math.floor() : Ця функція повертає найближче ціле число, менше або рівне заданому числу.
приклад : У цьому прикладі код нижче використовує бібліотеку `math` для обчислення максимальних значень для додатних і від’ємних десяткових дробів за допомогою `math.ceil` і мінімальних значень за допомогою `math.floor`. Виходи 5, 0, 2 і -1 для відповідних випадків.
python3
# import math library> import> math> # ceil value for positive> # decimal number> print> (math.ceil(> 4.2> ))> # ceil value for negative> # decimal number> print> (math.ceil(> -> 0.5> ))> # floor value for decimal> # and negative number> print> (math.floor(> 2.2> ))> print> (math.floor(> -> 0.5> ))> |
Вихід:
5 0 2 -1
Круглі числа в Python u співати math.ceil
Округлення числа передбачає зсув десяткової коми праворуч, округлення в більшу сторону, а потім зміщення її назад ліворуч для точності за допомогою ` math.ceil() ` і операції множення/ділення.
приклад : У цьому прикладі код нижче визначає функцію `round_up` за допомогою бібліотеки `math`, яка округлює число до вказаного десяткового знаку. Він використовує множення, округлення за допомогою `math.ceil()` і ділення для точності. Додатні та від’ємні значення перевіряються на округлення.
python3
# import math library> import> math> # define a function for> # round_up> def> round_up(n, decimals> => 0> ):> > multiplier> => 10> *> *> decimals> > return> math.ceil(n> *> multiplier)> /> multiplier> # passing positive values> print> (round_up(> 2.1> ))> print> (round_up(> 2.23> ,> 1> ))> print> (round_up(> 2.543> ,> 2> ))> # passing negative values> print> (round_up(> 22.45> ,> -> 1> ))> print> (round_up(> 2352> ,> -> 2> ))> |
Вихід:
3.0 2.3 2.55 30.0 2400.0
Ми можемо слідувати діаграмі нижче, щоб зрозуміти округлення в більшу та меншу сторону. Заокруглення вправо і вниз вліво.
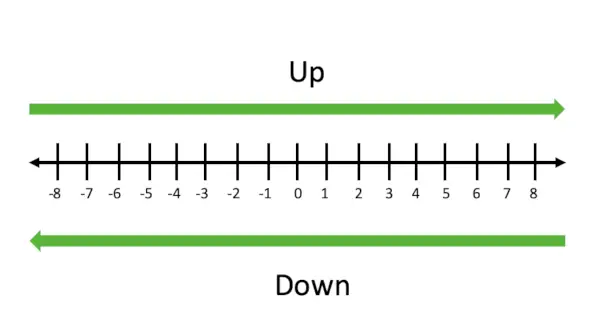
Округлення в більшу сторону завжди округлює число вправо на числовому рядку, а округлення вниз завжди округлює число вліво на числовій прямій.
Круглі числа в Python u співати мат.пов
У Rounding Down число округлюється до вказаної кількості цифр. Функцію округлення можна реалізувати таким чином:
- Спочатку кома в n зсувається на потрібну кількість знаків вправо шляхом множення n на 10 ** десяткових знаків.
- Нове значення округлюється до найближчого цілого числа за допомогою math.floor() .
- Нарешті, десяткова кома зсувається вліво шляхом ділення на 10 ** десяткових знаків.
python3
import> math> # defining a function for> # round down.> def> round_down(n, decimals> => 0> ):> > multiplier> => 10> *> *> decimals> > return> math.floor(n> *> multiplier)> /> multiplier> # passing different values to function> print> (round_down(> 2.5> ))> print> (round_down(> 2.48> ,> 1> ))> print> (round_down(> -> 0.5> ))> |
Вихід:
2.0 2.4 -1.0
Круглі числа в Python u співайте модуль Numpy
Модуль NumPy у Python забезпечує numpy.round()> функція округлити числа. Ця функція округлює кожен елемент масиву до найближчого цілого числа або до вказаної кількості десяткових знаків.
приклад: У цьому прикладі код нижче використовує модуль NumPy для створення масиву `arr` і округлює кожен елемент до найближчого цілого числа (`rounded_integers`) і до двох знаків після коми (`rounded_decimals`). Потім результати друкуються для відображення.
Python3
import> numpy as np> # Creating an array> arr> => np.array([> 1.234> ,> 2.567> ,> 3.789> ])> # Rounding each element to the nearest integer> rounded_integers> => np.> round> (arr)> # Rounding each element to two decimal places> rounded_decimals> => np.> round> (arr, decimals> => 2> )> # Displaying the results> print> (> 'Nearest integer:'> , rounded_integers)> print> (> 'Decimal places:'> , rounded_decimals)> |
Вихід:
Nearest integer: [1. 3. 4.] Decimal places: [1.23 2.57 3.79]
Круглі числа в Python u співати Ухил округлення концепція.
Концепція симетрії вводить поняття зміщення округлення, яке описує, як округлення впливає на числові дані в наборі даних.
Стратегія округлення має зміщення округлення до додатної нескінченності, оскільки значення завжди округлюється в напрямку додатної нескінченності. Подібним чином стратегія округлення має округлення до негативної нескінченності. Стратегія скорочення має зміщення до негативної нескінченності для позитивних значень і округлення до позитивної нескінченності для від’ємних значень. Кажуть, що функції округлення з такою поведінкою загалом мають округлення до нуля.
а) Округлення наполовину концепція в Python
Округлення наполовину округлює кожне число до найближчого числа із зазначеною точністю та розриває зв’язки шляхом округлення в більшу сторону.
Стратегія округлення наполовину реалізується шляхом зсуву десяткової коми вправо на потрібну кількість знаків. У цьому випадку нам доведеться визначити, чи є цифра після зміщеної коми меншою або більшою за 5.
Ми можемо додати 0,5 до значення, яке зсувається, а потім округлити його вниз за допомогою функції math.floor().
Реалізація функції round_half_up():
приклад: У цьому прикладі код нижче визначає `round_half_up`, спеціальну функцію округлення, яка використовує метод округлення наполовину вгору з `math.floor()` для точності. Демонстрації включають додатні та від’ємні числа з різними знаками після коми.
python3
import> math> # defining round_half_up> def> round_half_up(n, decimals> => 0> ):> > multiplier> => 10> *> *> decimals> > return> math.floor(n> *> multiplier> +> 0.5> )> /> multiplier> # passing different values to the function> print> (round_half_up(> 1.28> ,> 1> ))> print> (round_half_up(> -> 1.5> ))> print> (round_half_up(> -> 1.225> ,> 2> ))> |
Вихід:
1.3 -1.0 -1.23
б) Округлення наполовину вниз концепція в Python
Це округлення до найближчого числа подібно до методу округлення наполовину, відмінність полягає в тому, що він розриває зв’язки шляхом округлення до меншого з двох чисел. Стратегія округлення наполовину вниз реалізується шляхом заміни math.floor() у функції round_half_up() на math.ceil(), а потім шляхом віднімання 0,5 замість додавання.
Реалізація функції round_half_down():
У цьому прикладі наведений нижче код визначає `round_half_down` за допомогою бібліотеки `math` для досягнення поведінки округлення наполовину. Він використовує множення, віднімання та `math.ceil()` для округлення до нуля. Тестові випадки включають додатні та від’ємні десяткові дроби з округленням до одного знака після коми.
python3
# import math library> import> math> # defining a function> # for round_half_down> def> round_half_down(n, decimals> => 0> ):> > multiplier> => 10> *> *> decimals> > return> math.ceil(n> *> multiplier> -> 0.5> )> /> multiplier> # passing different values to the function> print> (round_half_down(> 2.5> ))> print> (round_half_down(> -> 2.5> ))> print> (round_half_down(> 2.25> ,> 1> ))> |
Вихід:
2.0 -3.0 2.2
Округлення половини від нуля в Python
У Округленні наполовину від нуля нам потрібно почати, як зазвичай, зі зсуву десяткової коми праворуч на певну кількість знаків, а потім помітити цифру (d) безпосередньо праворуч від десяткової коми в новому числі. Є чотири випадки для розгляду:
- Якщо n додатне і d>= 5, округліть у більшу сторону
- Якщо n додатне і d = 5, округліть униз
- Якщо n від’ємне і d>= 5, округліть униз
- Якщо n від’ємне і d <5, округліть у більшу сторону
Після округлення згідно з правилами, згаданими вище, ми можемо зсунути десятковий знак назад вліво.
- Округлення від половини до навіть: Існує спосіб пом’якшити зміщення округлення, коли ми округлюємо значення в наборі даних. Ми можемо просто округлити зв’язки до найближчого парного числа з бажаною точністю. Стратегія округлення від половини до рівного — це стратегія, яку використовує вбудований у Python round(). The десятковий клас підтримує швидку арифметику десяткових чисел з плаваючою комою з правильним округленням. Це дає кілька переваг перед типом даних float. Стандартною стратегією округлення в десятковому модулі є ROUND_HALF_EVEN.
приклад: У цьому прикладі код нижче використовує функцію `Decimal` з бібліотеки `decimal` для точного представлення десяткових чисел. Це контрастує створення об’єкта `Decimal` із рядка та безпосередньо з числа з плаваючою комою. Функція `quantize()` використовується для округлення з указаними десятковими знаками, демонструючи точність десяткової арифметики.
python3
# import Decimal function from> # decimal library> from> decimal> import> Decimal> print> (Decimal(> '0.1'> ))> print> (Decimal(> 0.1> ))> # Rounding a Decimal number is> # done with the .quantize() function> # '1.0' in .quantize() determines the> # number of decimal places to round the number> print> (Decimal(> '1.65'> ).quantize(Decimal(> '1.0'> )))> print> (Decimal(> '1.675'> ).quantize(Decimal(> '1.00'> )))> |
Вихід:
0.1 0.1000000000000000055511151231257827021181583404541015625 1.6 1.68