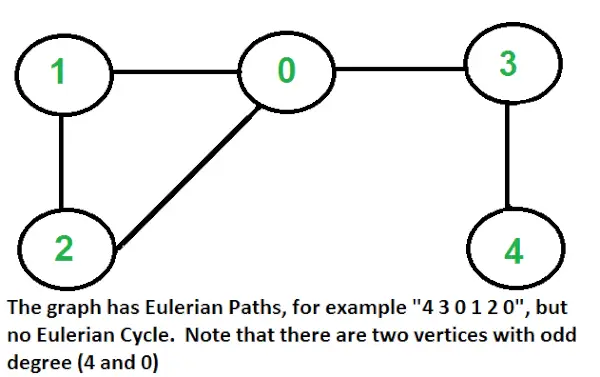
Шлях Ейлера це шлях у графі, який відвідує кожне ребро рівно один раз. Ейлерів контур — це ейлерів шлях, який починається й закінчується в одній вершині.

Як дізнатися, чи є заданий графік ейлеровим чи ні?

Проблема така ж, як і наступне запитання. Чи можна намалювати заданий графік, не відриваючи олівця від паперу та не обводячи жодного з країв більше одного разу.
Граф називається ейлеровим, якщо він має ейлерів цикл, і напівейлеровим, якщо він має ейлерів шлях. Проблема виглядає схожою на гамільтонів шлях, який є NP повною проблемою для загального графа. На щастя, ми можемо визначити, чи має даний графік ейлерів шлях чи ні, за поліноміальний час. Фактично, ми можемо знайти його за час O(V+E).
Нижче наведено деякі цікаві властивості неорієнтованих графів із ейлеровим шляхом і циклом. Ми можемо використовувати ці властивості, щоб визначити, чи є графік ейлеровим чи ні.

Цикл Ейлера: Неорієнтований граф має ейлерів цикл, якщо виконуються наступні дві умови.

1. Усі вершини з ненульовим степенем зв’язані. Нас не цікавлять вершини з нульовим ступенем, оскільки вони не належать до ейлерового циклу чи шляху (ми розглядаємо лише всі ребра).
2. Усі вершини мають парний ступінь.

Ейлерів шлях: Неорієнтований граф має ейлерів шлях, якщо виконуються наступні дві умови.

1. Те саме, що умова (а) для циклу Ейлера.
2. Якщо нуль або дві вершини мають непарний ступінь, а всі інші вершини мають парний ступінь. Зверніть увагу, що в неорієнтованому графі неможлива лише одна вершина з непарним ступенем (у неорієнтованому графі сума всіх ступенів завжди парна)

Зауважте, що граф без ребер вважається ейлеровим, оскільки немає ребер, які потрібно пройти.

Як це працює?
У ейлеровому шляху кожного разу, коли ми відвідуємо вершину v, ми проходимо через два невідвідані ребра з однією кінцевою точкою як v. Тому всі середні вершини в ейлеровому шляху повинні мати парний ступінь. Для циклу Ейлера будь-яка вершина може бути середньою вершиною, тому всі вершини повинні мати парний ступінь.

Рекомендована практика Схема Ейлера та шлях Спробуйте!

Реалізація:

C++

// A C++ program to check if a given graph is Eulerian or not> #include> #include> using> namespace> std;> // A class that represents an undirected graph> class> Graph> {> > int> V;> // No. of vertices> > list <> int> >*присл.;> // A dynamic array of adjacency lists> public> :> > // Constructor and destructor> > Graph(> int> V) {> this> ->V = V; adj => new> list <> int> >[IN]; }> > ~Graph() {> delete> [] adj; }> // To avoid memory leak> > // function to add an edge to graph> > void> addEdge(> int> v,> int> w);> > // Method to check if this graph is Eulerian or not> > int> isEulerian();> > // Method to check if all non-zero degree vertices are connected> > bool> isConnected();> > // Function to do DFS starting from v. Used in isConnected();> > void> DFSUtil(> int> v,> bool> visited[]);> };> void> Graph::addEdge(> int> v,> int> w)> {> > adj[v].push_back(w);> > adj[w].push_back(v);> // Note: the graph is undirected> }> void> Graph::DFSUtil(> int> v,> bool> visited[])> {> > // Mark the current node as visited and print it> > visited[v] => true> ;> > // Recur for all the vertices adjacent to this vertex> > list <> int> >::ітератор i;> > for> (i = adj[v].begin(); i != adj[v].end(); ++i)> > if> (!visited[*i])> > DFSUtil(*i, visited);> }> // Method to check if all non-zero degree vertices are connected.> // It mainly does DFS traversal starting from> bool> Graph::isConnected()> {> > // Mark all the vertices as not visited> > bool> visited[V];> > int> i;> > for> (i = 0; i visited[i] = false; // Find a vertex with non-zero degree for (i = 0; i if (adj[i].size() != 0) break; // If there are no edges in the graph, return true if (i == V) return true; // Start DFS traversal from a vertex with non-zero degree DFSUtil(i, visited); // Check if all non-zero degree vertices are visited for (i = 0; i if (visited[i] == false && adj[i].size()>0) повернути false; повернути істину; } /* Функція повертає одне з таких значень: 0 --> якщо графік не є ейлеровим 1 --> якщо графік має шлях Ейлера (напівейлерів) 2 --> якщо графік має контур Ейлера (ейлерів) */ int Graph::isEulerian() { // Перевірити, чи всі вершини ненульового ступеня з’єднані if (isConnected() == false) return 0; // Підрахувати вершини з непарним ступенем int odd = 0; for (int i = 0; i if (adj[i].size() & 1) odd++; // Якщо лічильник більше 2, то графік не є ейлеровим, якщо (odd> 2) повертає 0; // Якщо непарний // Якщо непарне число дорівнює 0, то ейлерове число ніколи не може бути 1 для неорієнтованого повернення графа 1 : 2; // Функція для виконання тестових випадків test(Graph &g) { int res = g.isEulerian(); if (res == 0) cout < < 'graph is not Eulerian '; else if (res == 1) cout < < 'graph has a Euler path '; else cout < < 'graph has a Euler cycle '; } // Driver program to test above function int main() { // Let us create and test graphs shown in above figures Graph g1(5); g1.addEdge(1, 0); g1.addEdge(0, 2); g1.addEdge(2, 1); g1.addEdge(0, 3); g1.addEdge(3, 4); test(g1); Graph g2(5); g2.addEdge(1, 0); g2.addEdge(0, 2); g2.addEdge(2, 1); g2.addEdge(0, 3); g2.addEdge(3, 4); g2.addEdge(4, 0); test(g2); Graph g3(5); g3.addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); test(g3); // Let us create a graph with 3 vertices // connected in the form of cycle Graph g4(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); test(g4); // Let us create a graph with all vertices // with zero degree Graph g5(3); test(g5); return 0; }>

Java

// A Java program to check if a given graph is Eulerian or not> import> java.io.*;> import> java.util.*;> import> java.util.LinkedList;> // This class represents an undirected graph using adjacency list> // representation> class> Graph> {> > private> int> V;> // No. of vertices> > // Array of lists for Adjacency List Representation> > private> LinkedList adj[];> > // Constructor> > Graph(> int> v)> > {> > V = v;> > adj => new> LinkedList[v];> > for> (> int> i=> 0> ; i adj[i] = new LinkedList(); } //Function to add an edge into the graph void addEdge(int v, int w) { adj[v].add(w);// Add w to v's list. adj[w].add(v); //The graph is undirected } // A function used by DFS void DFSUtil(int v,boolean visited[]) { // Mark the current node as visited visited[v] = true; // Recur for all the vertices adjacent to this vertex Iterator i = adj[v].listIterator(); while (i.hasNext()) { int n = i.next(); if (!visited[n]) DFSUtil(n, visited); } } // Method to check if all non-zero degree vertices are // connected. It mainly does DFS traversal starting from boolean isConnected() { // Mark all the vertices as not visited boolean visited[] = new boolean[V]; int i; for (i = 0; i visited[i] = false; // Find a vertex with non-zero degree for (i = 0; i if (adj[i].size() != 0) break; // If there are no edges in the graph, return true if (i == V) return true; // Start DFS traversal from a vertex with non-zero degree DFSUtil(i, visited); // Check if all non-zero degree vertices are visited for (i = 0; i if (visited[i] == false && adj[i].size()>0) повернути false; повернути істину; } /* Функція повертає одне з таких значень: 0 --> якщо графік не є ейлеровим 1 --> якщо графік має шлях Ейлера (напівейлерів) 2 --> якщо графік має контур Ейлера (ейлерів) */ int isEulerian() { // Перевірити, чи всі вершини ненульового ступеня з’єднані if (isConnected() == false) return 0; // Підрахувати вершини з непарним ступенем int odd = 0; for (int i = 0; i if (adj[i].size()%2!=0) odd++; // Якщо лічильник більше 2, то графік не є ейлеровим, якщо (odd> 2) повертає 0; / / Якщо непарне число дорівнює 2, то непарне число дорівнює 0, // Зверніть увагу, що непарне число ніколи не може бути 1 для неорієнтованого графіка (непарне==2) Функція для виконання тестів void test() { int res = isEulerian(); if (res == 0) System.out.println('graph is not Eulerian'); else if (res == 1) System. out.println('graph has a Euler path'); else System.out.println('graph has a Euler cycle' } // Метод драйвера public static void main(String args[]) { / / Давайте створимо та перевіримо графіки, показані на малюнках вище: g1.addEdge(1, 0); (0, 3); g1.addEdge (0, 2); g2.addEdge (0, 2); addEdge(2, 1); g2.addEdge(3, 4); g2.test(5); .addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); g3.test(); // Створимо граф із 3 вершинами // з’єднаними у вигляді циклу Graph g4 = new Graph(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); g4.test(); // Створимо граф з усіма вершинами // з нульовим ступенем Graph g5 = new Graph(3); g5.test(); } } // Цей код створено Aakash Hasija>

Python3

# Python program to check if a given graph is Eulerian or not> #Complexity : O(V+E)> from> collections> import> defaultdict> # This class represents a undirected graph using adjacency list representation> class> Graph:> > def> __init__(> self> , vertices):> > self> .V> => vertices> # No. of vertices> > self> .graph> => defaultdict(> list> )> # default dictionary to store graph> > # function to add an edge to graph> > def> addEdge(> self> , u, v):> > self> .graph[u].append(v)> > self> .graph[v].append(u)> > # A function used by isConnected> > def> DFSUtil(> self> , v, visited):> > # Mark the current node as visited> > visited[v]> => True> > # Recur for all the vertices adjacent to this vertex> > for> i> in> self> .graph[v]:> > if> visited[i]> => => False> :> > self> .DFSUtil(i, visited)> > '''Method to check if all non-zero degree vertices are> > connected. It mainly does DFS traversal starting from> > node with non-zero degree'''> > def> isConnected(> self> ):> > # Mark all the vertices as not visited> > visited> => [> False> ]> *> (> self> .V)> > # Find a vertex with non-zero degree> > for> i> in> range> (> self> .V):> > if> len> (> self> .graph[i]) !> => 0> :> > break> > # If there are no edges in the graph, return true> > if> i> => => self> .V> -> 1> :> > return> True> > # Start DFS traversal from a vertex with non-zero degree> > self> .DFSUtil(i, visited)> > # Check if all non-zero degree vertices are visited> > for> i> in> range> (> self> .V):> > if> visited[i]> => => False> and> len> (> self> .graph[i])>> 0> :> > return> False> > return> True> > '''The function returns one of the following values> > 0 -->Якщо графік не є ейлеровим> > 1 -->Якщо графік має шлях Ейлера (напівейлерів)> > 2 -->Якщо граф має контур Ейлера (ейлерів) '''> > def> isEulerian(> self> ):> > # Check if all non-zero degree vertices are connected> > if> self> .isConnected()> => => False> :> > return> 0> > else> :> > # Count vertices with odd degree> > odd> => 0> > for> i> in> range> (> self> .V):> > if> len> (> self> .graph[i])> %> 2> !> => 0> :> > odd> +> => 1> > '''If odd count is 2, then semi-eulerian.> > If odd count is 0, then eulerian> > If count is more than 2, then graph is not Eulerian> > Note that odd count can never be 1 for undirected graph'''> > if> odd> => => 0> :> > return> 2> > elif> odd> => => 2> :> > return> 1> > elif> odd>> 2> :> > return> 0> > # Function to run test cases> > def> test(> self> ):> > res> => self> .isEulerian()> > if> res> => => 0> :> > print> (> 'graph is not Eulerian'> )> > elif> res> => => 1> :> > print> (> 'graph has a Euler path'> )> > else> :> > print> (> 'graph has a Euler cycle'> )> # Let us create and test graphs shown in above figures> g1> => Graph(> 5> )> g1.addEdge(> 1> ,> 0> )> g1.addEdge(> 0> ,> 2> )> g1.addEdge(> 2> ,> 1> )> g1.addEdge(> 0> ,> 3> )> g1.addEdge(> 3> ,> 4> )> g1.test()> g2> => Graph(> 5> )> g2.addEdge(> 1> ,> 0> )> g2.addEdge(> 0> ,> 2> )> g2.addEdge(> 2> ,> 1> )> g2.addEdge(> 0> ,> 3> )> g2.addEdge(> 3> ,> 4> )> g2.addEdge(> 4> ,> 0> )> g2.test()> g3> => Graph(> 5> )> g3.addEdge(> 1> ,> 0> )> g3.addEdge(> 0> ,> 2> )> g3.addEdge(> 2> ,> 1> )> g3.addEdge(> 0> ,> 3> )> g3.addEdge(> 3> ,> 4> )> g3.addEdge(> 1> ,> 3> )> g3.test()> # Let us create a graph with 3 vertices> # connected in the form of cycle> g4> => Graph(> 3> )> g4.addEdge(> 0> ,> 1> )> g4.addEdge(> 1> ,> 2> )> g4.addEdge(> 2> ,> 0> )> g4.test()> # Let us create a graph with all vertices> # with zero degree> g5> => Graph(> 3> )> g5.test()> # This code is contributed by Neelam Yadav>

C#

// A C# program to check if a given graph is Eulerian or not> using> System;> using> System.Collections.Generic;> > // This class represents an undirected graph using adjacency list> // representation> public> class> Graph> {> > private> int> V;> // No. of vertices> > > // Array of lists for Adjacency List Representation> > private> List <> int> >[]присл.;> > > // Constructor> > Graph(> int> v)> > {> > V = v;> > adj => new> List <> int> >[в];> > for> (> int> i=0; i adj[i] = new List (); } //Функція для додавання ребра в граф void addEdge(int v, int w) { adj[v].Add(w);// Додати w до списку v. adj[w].Add(v); //Графік не орієнтований } // Функція, яку використовує DFS void DFSUtil(int v,bool []visited) { // Позначити поточний вузол як відвіданий visited[v] = true; // Повторюється для всіх вершин, суміжних із цією вершиною foreach(int i in adj[v]){ int n = i; if (!visited[n]) DFSUtil(n, visited); } } // Метод перевірки, чи всі вершини ненульового ступеня // з'єднані. Здебільшого виконує обхід DFS, починаючи з bool isConnected() { // Позначити всі вершини як невідвідані bool []visited = new bool[V]; int i; for (i = 0; i visited[i] = false; // Знайти вершину з ненульовим ступенем for (i = 0; i if (adj[i].Count != 0) break; // Якщо є немає ребер у графі, повертає істину, якщо (i == V) повертає істину; // Почати обхід DFS з вершини з ненульовим ступенем DFSUtil(i, visited); // Перевірити, чи відвідано всі ненульові вершини for (i = 0; i if (visited[i] == false && adj[i].Count> 0) return false; return true; } /* Функція повертає одне з таких значень 0 --> Якщо графік є не ейлерів 1 --> якщо граф має ейлерів шлях (напівейлерів) 2 --> якщо граф має ейлерів контур (ейлерів) */ int isEulerian() { // перевірити, чи всі вершини ненульового ступеня з’єднані, якщо (isConnected() == false) return 0; // Підрахувати вершини з непарним ступенем int odd = 0; for (int i = 0; i if (adj[i].Count%2!=0) odd++; // If число більше 2, тоді графік не є ейлеровим, якщо (непарне> 2) повертає 0; // Якщо непарне число дорівнює 2, то // якщо непарне число дорівнює 0, // Зауважте, що непарне число може ніколи не буде 1 для неорієнтованого повернення графа (непарний==2)? 1 : 2; } // Функція для запуску тестів void test() { int res = isEulerian(); if (res == 0) Console.WriteLine('графік не є ейлеровим'); else if (res == 1) Console.WriteLine('графік має шлях Ейлера'); else Console.WriteLine('граф має цикл Ейлера'); } // Метод драйвера public static void Main(String []args) { // Давайте створимо та протестуємо графіки, показані на малюнках вище Graph g1 = new Graph(5); g1.addEdge(1, 0); g1.addEdge(0, 2); g1.addEdge(2, 1); g1.addEdge(0, 3); g1.addEdge(3, 4); g1.test(); Графік g2 = новий графік (5); g2.addEdge(1, 0); g2.addEdge(0, 2); g2.addEdge(2, 1); g2.addEdge(0, 3); g2.addEdge(3, 4); g2.addEdge(4, 0); g2.test(); Графік g3 = новий графік (5); g3.addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); g3.test(); // Створимо граф із 3 вершинами // з’єднаними у вигляді циклу Graph g4 = new Graph(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); g4.test(); // Створимо граф з усіма вершинами // з нульовим ступенем Graph g5 = new Graph(3); g5.test(); } } // Цей код надав PrinciRaj1992>

Javascript

> // A Javascript program to check if a given graph is Eulerian or not> // This class represents an undirected graph using adjacency list> // representation> class Graph> {> > // Constructor> > constructor(v)> > {> > this> .V = v;> > this> .adj => new> Array(v);> > for> (let i = 0; i this.adj[i] = []; } // Function to add an edge into the graph addEdge(v,w) { this.adj[v].push(w);// Add w to v's list. this.adj[w].push(v); //The graph is undirected } // A function used by DFS DFSUtil(v,visited) { // Mark the current node as visited visited[v] = true; // Recur for all the vertices adjacent to this vertex for(let i of this.adj[v]) { let n = i; if (!visited[n]) this.DFSUtil(n, visited); } } // Method to check if all non-zero degree vertices are // connected. It mainly does DFS traversal starting from isConnected() { // Mark all the vertices as not visited let visited = new Array(this.V); let i; for (i = 0; i 0) повернути false; повернути істину; } /* Функція повертає одне з таких значень: 0 --> якщо графік не є ейлеровим 1 --> якщо графік має шлях Ейлера (напівейлерів) 2 --> якщо графік має схему Ейлера (ейлерів) */ isEulerian() { // Перевірити, чи всі вершини ненульового ступеня з’єднані if (this.isConnected() == false) return 0; // Підрахувати вершини з непарним ступенем let odd = 0; для (нехай i = 0; i 2) повернути 0; // Якщо непарна кількість дорівнює 2, то напівейлер. // Якщо непарна кількість дорівнює 0, тоді ейлерів // Зауважте, що непарна кількість ніколи не може бути 1 для неорієнтованого повернення графа (непарний==2)? 1 : 2; } // Функція для запуску тестових випадків test() { let res = this.isEulerian(); if (res == 0) document.write('графік не є ейлеровим '); else if (res == 1) document.write('граф має шлях Ейлера '); else document.write('граф має цикл Ейлера'); } } // Метод драйвера // Давайте створимо та перевіримо графіки, показані на малюнках вище let g1 = new Graph(5); g1.addEdge(1, 0); g1.addEdge(0, 2); g1.addEdge(2, 1); g1.addEdge(0, 3); g1.addEdge(3, 4); g1.test(); нехай g2 = новий графік (5); g2.addEdge(1, 0); g2.addEdge(0, 2); g2.addEdge(2, 1); g2.addEdge(0, 3); g2.addEdge(3, 4); g2.addEdge(4, 0); g2.test(); нехай g3 = новий графік (5); g3.addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); g3.test(); // Створимо граф із 3 вершинами // з’єднаними у вигляді циклу let g4 = new Graph(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); g4.test(); // Створимо граф з усіма вершинами // з нульовим ступенем let g5 = new Graph(3); g5.test(); // Цей код створено avanitrachhadiya2155>

Вихід

graph has a Euler path graph has a Euler cycle graph is not Eulerian graph has a Euler cycle graph has a Euler cycle 

Часова складність: O(V+E)

Просторова складність: O(V+E)

Наступні статті:
Ейлерів шлях і схема для орієнтованих графів.
Алгоритм Флері для друку ейлерового шляху або схеми?