АЛГОРИТМИ ЕВКЛІДА (БАЗОВІ ТА РОЗШИРЕНІ) - TECHCODEVIEW.COM

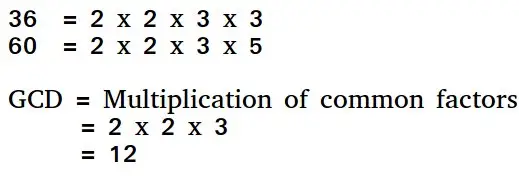
Алгоритм Евкліда — це спосіб знайти найбільший спільний дільник двох натуральних чисел. НОД двох чисел — це найбільше число, яке ділить їх обидва. Простий спосіб знайти НОД — розкласти обидва числа на множники та помножити загальні прості множники.

НОД

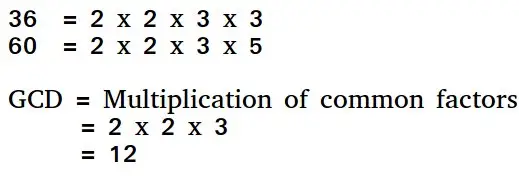
Базовий алгоритм Евкліда для НОД:

Алгоритм базується на наведених нижче фактах.

Якщо ми віднімаємо менше число від більшого (зменшуємо більше число), НОД не змінюється. Отже, якщо ми будемо постійно віднімати більше з двох, ми отримаємо НОД.
Тепер замість віднімання, якщо ми ділимо менше число, алгоритм зупиняється, коли ми знаходимо залишок 0.

Нижче наведено рекурсивну функцію для оцінки gcd за допомогою алгоритму Евкліда:

C

// C program to demonstrate Basic Euclidean Algorithm> #include> // Function to return gcd of a and b> int> gcd(> int> a,> int> b)> {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> }> // Driver code> int> main()> {> > int> a = 10, b = 15;> > > // Function call> > printf> (>

'GCD(%d, %d) = %d
'>

, a, b, gcd(a, b));> > a = 35, b = 10;> > printf> (>

'GCD(%d, %d) = %d
'>

, a, b, gcd(a, b));> > a = 31, b = 2;> > printf> (>

'GCD(%d, %d) = %d
'>

, a, b, gcd(a, b));> > return> 0;> }>

CPP

// C++ program to demonstrate> // Basic Euclidean Algorithm> #include> using> namespace> std;> // Function to return> // gcd of a and b> int> gcd(> int> a,> int> b)> {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> }> // Driver Code> int> main()> {> > int> a = 10, b = 15;> > > // Function call> > cout < <> 'GCD('> < < a < <> ', '> < < b < <> ') = '> < < gcd(a, b)> > < < endl;> > a = 35, b = 10;> > cout < <> 'GCD('> < < a < <> ', '> < < b < <> ') = '> < < gcd(a, b)> > < < endl;> > a = 31, b = 2;> > cout < <> 'GCD('> < < a < <> ', '> < < b < <> ') = '> < < gcd(a, b)> > < < endl;> > return> 0;> }>

Java

// Java program to demonstrate Basic Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> > // extended Euclidean Algorithm> > public> static> int> gcd(> int> a,> int> b)> > {> > if> (a ==> 0> )> > return> b;> > return> gcd(b % a, a);> > }> > // Driver code> > public> static> void> main(String[] args)> > {> > int> a => 10> , b => 15> , g;> > > // Function call> > g = gcd(a, b);> > System.out.println(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a => 35> ;> > b => 10> ;> > g = gcd(a, b);> > System.out.println(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a => 31> ;> > b => 2> ;> > g = gcd(a, b);> > System.out.println(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > }> }> // Code Contributed by Mohit Gupta_OMG>

Python3

# Python3 program to demonstrate Basic Euclidean Algorithm> # Function to return gcd of a and b> def> gcd(a, b):> > if> a> => => 0> :> > return> b> > return> gcd(b> %> a, a)> # Driver code> if> __name__> => => '__main__'> :> > a> => 10> > b> => 15> > print> (> 'gcd('> , a,> ','> , b,> ') = '> , gcd(a, b))> > a> => 35> > b> => 10> > print> (> 'gcd('> , a,> ','> , b,> ') = '> , gcd(a, b))> > a> => 31> > b> => 2> > print> (> 'gcd('> , a,> ','> , b,> ') = '> , gcd(a, b))> # Code Contributed By Mohit Gupta_OMG>

C#

// C# program to demonstrate Basic Euclidean Algorithm> using> System;> class> GFG {> > public> static> int> gcd(> int> a,> int> b)> > {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> > }> > // Driver Code> > static> public> void> Main()> > {> > int> a = 10, b = 15, g;> > g = gcd(a, b);> > Console.WriteLine(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a = 35;> > b = 10;> > g = gcd(a, b);> > Console.WriteLine(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a = 31;> > b = 2;> > g = gcd(a, b);> > Console.WriteLine(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > }> }> // This code is contributed by ajit>

PHP

// php program to demonstrate Basic Euclidean Algorithm>

 // PHP program to demonstrate // Basic Euclidean Algorithm // Function to return // gcd of a and b function gcd($a, $b) {  if ($a == 0)  return $b;  return gcd($b % $a, $a); } // Driver Code $a = 10; $b = 15; // Function call echo 'GCD(',$a,',' , $b,') = ',   gcd($a, $b); echo '
'; $a = 35; $b = 10; echo 'GCD(',$a ,',',$b,') = ',   gcd($a, $b); echo '
'; $a = 31; $b = 2; echo 'GCD(',$a ,',', $b,') = ',   gcd($a, $b); // This code is contributed by m_kit ?>>

Javascript

// JavaScript program to demonstrate> // Basic Euclidean Algorithm> // Function to return> // gcd of a and b> function> gcd( a, b)> {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> }> // Driver Code> > let a = 10, b = 15;> > document.write(> 'GCD('> + a +> ', '> > + b +> ') = '> + gcd(a, b) +> ' '> );> > > a = 35, b = 10;> > document.write(> 'GCD('> + a +> ', '> > + b +> ') = '> + gcd(a, b) +> ' '> );> > > a = 31, b = 2;> > document.write(> 'GCD('> + a +> ', '> > + b +> ') = '> + gcd(a, b) +> ' '> );> // This code contributed by aashish1995>

Вихід

GCD(10, 15) = 5 GCD(35, 10) = 5 GCD(31, 2) = 1

Часова складність: O(Log min(a, b))
Допоміжний простір: O(Log (min(a,b))

Розширений алгоритм Евкліда:

Розширений алгоритм Евкліда також знаходить цілі коефіцієнти x і y такі, що: ax + by = gcd(a, b)

приклади:

введення: a = 30, b = 20
Вихід: gcd = 10, x = 1, y = -1
(Зверніть увагу, що 30*1 + 20*(-1) = 10)

введення: a = 35, b = 15
Вихід: gcd = 5, x = 1, y = -2
(Зверніть увагу, що 35*1 + 15*(-2) = 5)

Розширений алгоритм Евкліда оновлює результати gcd(a, b), використовуючи результати, обчислені за допомогою рекурсивного виклику gcd(b%a, a). Нехай значення x і y, обчислені за допомогою рекурсивного виклику, дорівнюють x ₁і у ₁. x і y оновлюються за допомогою наведених нижче виразів.

ax + by = gcd(a, b)
gcd(a, b) = gcd(b%a, a)
gcd(b%a, a) = (b%a)x ₁+ є ₁
ax + by = (b%a)x ₁+ є ₁
ax + by = (b – [b/a] * a)x ₁+ є ₁
ax + by = a(y ₁– [б/а] * х ₁) + bx ₁

Порівнюючи LHS і RHS,
х = у ₁– ?b/a? * x ₁
y = x ₁

Рекомендована практика Розширений алгоритм Евкліда Спробуйте!

Нижче наведено реалізацію вищезазначеного підходу:

C++

// C++ program to demonstrate working of> // extended Euclidean Algorithm> #include> using> namespace> std;> // Function for extended Euclidean Algorithm> int> gcdExtended(> int> a,> int> b,> int> *x,> int> *y)> {> > // Base Case> > if> (a == 0)> > {> > *x = 0;> > *y = 1;> > return> b;> > }> > int> x1, y1;> // To store results of recursive call> > int> gcd = gcdExtended(b%a, a, &x1, &y1);> > // Update x and y using results of> > // recursive call> > *x = y1 - (b/a) * x1;> > *y = x1;> > return> gcd;> }> // Driver Code> int> main()> {> > int> x, y, a = 35, b = 15;> > int> g = gcdExtended(a, b, &x, &y);> > cout < <> 'GCD('> < < a < <> ', '> < < b> > < <> ') = '> < < g < < endl;> > return> 0;> }>

C

// C program to demonstrate working of extended> // Euclidean Algorithm> #include> // C function for extended Euclidean Algorithm> int> gcdExtended(> int> a,> int> b,> int> *x,> int> *y)> {> > // Base Case> > if> (a == 0)> > {> > *x = 0;> > *y = 1;> > return> b;> > }> > int> x1, y1;> // To store results of recursive call> > int> gcd = gcdExtended(b%a, a, &x1, &y1);> > // Update x and y using results of recursive> > // call> > *x = y1 - (b/a) * x1;> > *y = x1;> > return> gcd;> }> // Driver Program> int> main()> {> > int> x, y;> > int> a = 35, b = 15;> > int> g = gcdExtended(a, b, &x, &y);> > printf> (> 'gcd(%d, %d) = %d'> , a, b, g);> > return> 0;> }>

Java

// Java program to demonstrate working of extended> // Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> > // extended Euclidean Algorithm> > public> static> int> gcdExtended(> int> a,> int> b,> int> x,> > int> y)> > {> > // Base Case> > if> (a ==> 0> ) {> > x => 0> ;> > y => 1> ;> > return> b;> > }> > int> x1 => 1> ,> > y1 => 1> ;> // To store results of recursive call> > int> gcd = gcdExtended(b % a, a, x1, y1);> > // Update x and y using results of recursive> > // call> > x = y1 - (b / a) * x1;> > y = x1;> > return> gcd;> > }> > // Driver Program> > public> static> void> main(String[] args)> > {> > int> x => 1> , y => 1> ;> > int> a => 35> , b => 15> ;> > int> g = gcdExtended(a, b, x, y);> > System.out.print(> 'gcd('> + a +> ' , '> + b> > +> ') = '> + g);> > }> }>

Python3

# Python program to demonstrate working of extended> # Euclidean Algorithm> # function for extended Euclidean Algorithm> def> gcdExtended(a, b):> > # Base Case> > if> a> => => 0> :> > return> b,> 0> ,> 1> > gcd, x1, y1> => gcdExtended(b> %> a, a)> > # Update x and y using results of recursive> > # call> > x> => y1> -> (b> /> /> a)> *> x1> > y> => x1> > return> gcd, x, y> # Driver code> a, b> => 35> ,> 15> g, x, y> => gcdExtended(a, b)> print> (> 'gcd('> , a,> ','> , b,> ') = '> , g)>

C#

// C# program to demonstrate working> // of extended Euclidean Algorithm> using> System;> class> GFG> {> > > // extended Euclidean Algorithm> > public> static> int> gcdExtended(> int> a,> int> b,> > int> x,> int> y)> > {> > // Base Case> > if> (a == 0)> > {> > x = 0;> > y = 1;> > return> b;> > }> > // To store results of> > // recursive call> > int> x1 = 1, y1 = 1;> > int> gcd = gcdExtended(b % a, a, x1, y1);> > // Update x and y using> > // results of recursive call> > x = y1 - (b / a) * x1;> > y = x1;> > return> gcd;> > }> > > // Driver Code> > static> public> void> Main ()> > {> > int> x = 1, y = 1;> > int> a = 35, b = 15;> > int> g = gcdExtended(a, b, x, y);> > Console.WriteLine(> 'gcd('> + a +> ' , '> +> > b +> ') = '> + g);> > }> }>

PHP

 // PHP program to demonstrate  // working of extended  // Euclidean Algorithm // PHP function for  // extended Euclidean  // Algorithm function gcdExtended($a, $b,   $x, $y) {  // Base Case  if ($a == 0)  {  $x = 0;  $y = 1;  return $b;  }  // To store results   // of recursive call  $gcd = gcdExtended($b % $a,   $a, $x, $y);  // Update x and y using  // results of recursive  // call  $x = $y - floor($b / $a) * $x;  $y = $x;  return $gcd; } // Driver Code $x = 0; $y = 0; $a = 35; $b = 15; $g = gcdExtended($a, $b, $x, $y); echo 'gcd(',$a; echo ', ' , $b, ')'; echo ' = ' , $g; ?>>

Javascript

> // Javascript program to demonstrate> // working of extended> // Euclidean Algorithm> // Javascript function for> // extended Euclidean> // Algorithm> function> gcdExtended(a, b,> > x, y)> {> > // Base Case> > if> (a == 0)> > {> > x = 0;> > y = 1;> > return> b;> > }> > // To store results> > // of recursive call> > let gcd = gcdExtended(b % a,> > a, x, y);> > // Update x and y using> > // results of recursive> > // call> > x = y - (b / a) * x;> > y = x;> > return> gcd;> }> // Driver Code> let x = 0;> let y = 0;> let a = 35;> let b = 15;> let g = gcdExtended(a, b, x, y);> document.write(> 'gcd('> + a);> document.write(> ', '> + b +> ')'> );> document.write(> ' = '> + g);> >

Вихід:

gcd(35, 15) = 5

Часова складність: O(log N)
Допоміжний простір: O(log N)

Як працює розширений алгоритм?

Як видно вище, x і y є результатами для входів a і b,

a.x + b.y = gcd —-(1)

І х ₁і у ₁є результатами для входів b%a і a

(b%a).x ₁+ а.у ₁= gcd

Коли ми поставимо b%a = (b – (?b/a?).a) вище,
ми отримуємо слідування. Зауважте, що ?b/a? поверх (б/п)

(b – (?b/a?).a).x ₁+ а.у ₁= gcd

Наведене вище рівняння також можна записати, як показано нижче

б.х ₁+ а.(і ₁– (?b/a?).x ₁) = gcd —(2)

Після порівняння коефіцієнтів «a» і «b» в (1) і
(2) отримуємо наступне
х = у ₁– ?b/a? * x ₁
y = x ₁

Чим корисний розширений алгоритм?

Розширений алгоритм Евкліда особливо корисний, коли a і b є взаємно простими (або gcd дорівнює 1). Оскільки x є модульним мультиплікативним оберненим до a за модулем b, а y є модульним мультиплікативним оберненим до b по модулю a. Зокрема, обчислення модульного мультиплікативного зворотного є важливим кроком у методі шифрування з відкритим ключем RSA.