Перетворення двійкового коду в код Грея

Перетворювач двійкового коду в код Грея – це логічна схема, яка використовується для перетворення двійкового коду в його еквівалентний код Грея. Розмістивши MSB 1 нижче осі та MSB 1 над віссю та відображаючи (n-1) бітовий код щодо осі після 2 n-1 рядків, ми можемо отримати n-розрядний код Грея.
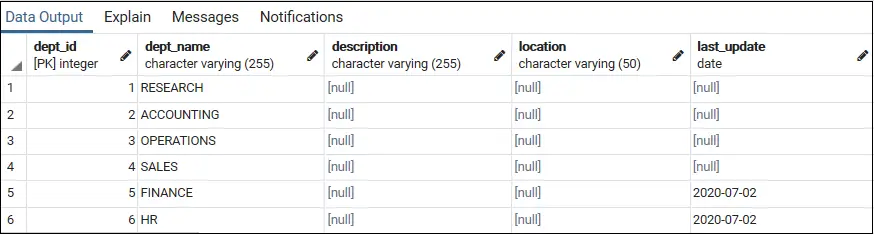
Таблиця перетворення 4-розрядного двійкового коду в код Грея виглядає наступним чином:
| Десяткове число | 4-розрядний двійковий код | 4-бітний код Грея |
|---|---|---|
| А Б В Г | Г 1 Г 2 Г 3 Г 4 | |
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| одинадцять | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| п'ятнадцять | 1111 | 1000 |
У 4-бітовому коді сірого 3-бітний код відображається на осі, проведеній після 2 4-1 -1 тис =8 тис рядок.

Як перетворити двійковий код на код Грея
- У коді Грея MSB завжди буде таким самим, як і 1-й біт даного двійкового числа.
- Щоб виконати 2 nd біт коду Грея, ми виконуємо виключаюче або (XOR) 1-го та 2-го nd біт двійкового числа. Це означає, що якщо обидва біти різні, результат буде один, інший результат буде 0.
- Щоб отримати 3 rd біт коду Грея, нам потрібно виконати виключаюче або (XOR) 2 nd і 3 rd біт двійкового числа. Процес залишається тим самим для 4 тис біт коду Грея. Розглянемо приклад, щоб зрозуміти ці кроки.
приклад
Припустимо, у нас є двійкове число 01101, яке ми хочемо перетворити на код Грея. Щоб виконати це перетворення, потрібно виконати наступні дії:
- Як ми знаємо, що 1 вул біт коду Грея такий самий, як MSB двійкового числа. У нашому прикладі MSB дорівнює 0, тому MSB або 1 вул біт коду сірого дорівнює 0.
- Далі ми виконуємо операцію XOR 1-го та другого двійкового числа. 1 вул біт дорівнює 0, а 2 nd біт дорівнює 1. Обидва біти різні, тому 2 nd біт коду Грея дорівнює 1.
- Тепер ми виконуємо XOR 2 nd біт і 3 rd біт двійкового числа. 2 nd біт дорівнює 1, а 3 rd біт також дорівнює 1. Ці біти однакові, тому 3 rd біт коду Грея дорівнює 0.
- Знову виконайте операцію XOR 3 rd і 4 тис біт двійкового числа. 3 rd біт дорівнює 1, а 4 тис біт дорівнює 0. Оскільки вони різні, 4 тис біт коду Грея дорівнює 1.
- Нарешті, виконайте XOR з 4 тис біт і 5 тис біт двійкового числа. 4 тис біт дорівнює 0, а 5 тис біт дорівнює 1. Обидва біти різні, тому 5 тис біт коду Грея дорівнює 1.
- Сірим кодом двійкового числа 01101 є 01011.

Перетворення Грея в двійковий код
Перетворювач коду Грея в двійковий — це логічна схема, яка використовується для перетворення коду Грея в еквівалентний двійковий код. Для перетворення коду Грея в двійкове число використовується наступна схема.

Так само, як перетворення двійкового коду в код Грея; це також дуже простий процес. Для перетворення коду Грея в двійковий код використовуються такі кроки.
- Так само, як від двійкового до сірого, від сірого до двійкового, 1 вул біт двійкового числа подібний до MSB коду Грея.
- 2 nd біт двійкового числа збігається з 1 вул біт двійкового числа, коли 2 nd біт коду Грея дорівнює 0; інакше 2 nd біт змінено біт 1 вул біт двійкового числа. Це означає, що 1 вул біт двійкового коду дорівнює 1, потім 2 nd біт дорівнює 0, а якщо він дорівнює 0, то 2 nd трохи бути 1.
- 2 nd крок продовжується для всіх бітів двійкового числа.

Приклад перетворення коду Грея в двійковий
Припустимо, у нас є код Грея 01011, який ми хочемо перетворити на двійкове число. Для перетворення нам потрібно виконати наступні кроки:
- Перший біт двійкового числа такий самий, як MSB коду Грея. MSB коду Грея дорівнює 0, тому MSB двійкового числа дорівнює 0.
- Тепер для 2 nd біт, ми перевіряємо 2 nd біт коду Грея. 2 nd біт коду Грея дорівнює 1, тому 2 nd біт двійкового числа - це змінене число 1 вул
- Наступний біт коду Грея дорівнює 0; 3 rd біт такий самий, як 2 nd біт коду Грея, тобто 1.
- 4 тис біт коду Грея дорівнює 1; 4 тис бітом двійкового числа є 0, що є зміненим числом 3 rd
- 5 тис біт коду Грея дорівнює 1; 5 тис розрядність двійкового числа дорівнює 1; це змінене число 4 тис біт двійкового числа.
- Отже, двійкове число коду Грея 01011 дорівнює 01101.
Біти 4-бітного коду Грея розглядаються як G 4 Г 3 Г 2 Г 1 . Тепер із таблиці перетворення,

The Карти Карно (K-карти) для G 4 , Г 3 , Г 2, і Г 1 такі: