Arbre indexé binaire bidimensionnel ou arbre Fenwick
Prérequis - Arbre Fenwick
Nous savons que pour répondre efficacement aux requêtes de somme de plage sur un tableau 1D, l'arbre à index binaire (ou arbre de Fenwick) est le meilleur choix (encore meilleur que l'arbre à segments en raison de moins de besoins en mémoire et un peu plus rapide que l'arbre à segments).
Pouvons-nous répondre efficacement aux requêtes de somme de sous-matrice en utilisant l'arbre indexé binaire ?
La réponse est Oui . Ceci est possible en utilisant un BITS 2D qui n'est rien d'autre qu'un tableau de BIT 1D.
Algorithme:
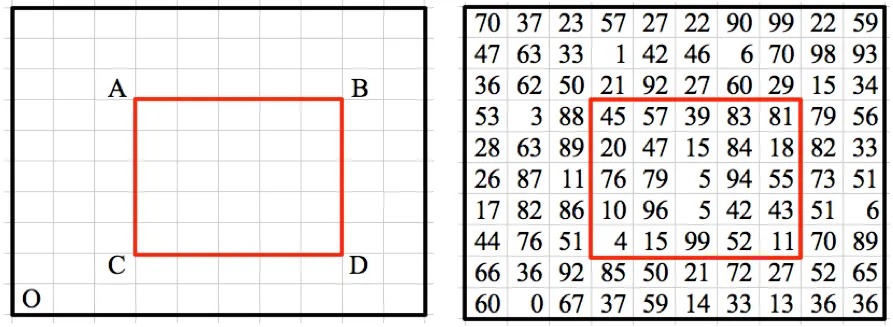
Nous considérons l'exemple ci-dessous. Supposons que nous devions trouver la somme de tous les nombres à l’intérieur de la zone en surbrillance :

Nous supposons l'origine de la matrice en bas - O. Ensuite, un BIT 2D exploite le fait que -
Sum under the marked area = Sum(OB) - Sum(OD) - Sum(OA) + Sum(OC)
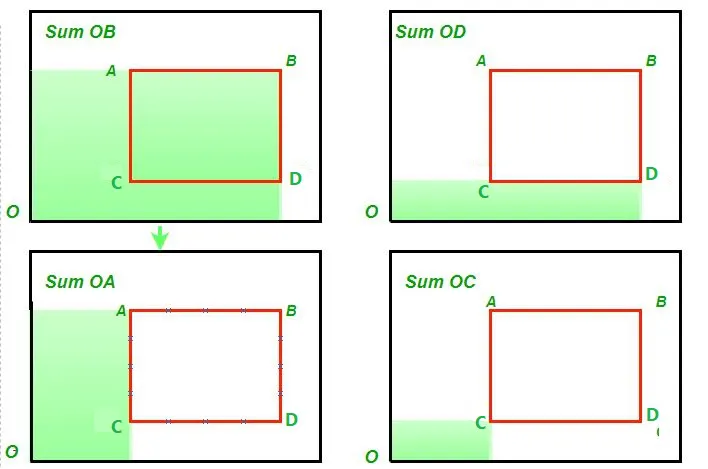
Dans notre programme, nous utilisons la fonction getSum(x y) qui trouve la somme de la matrice de (0 0) à (x y).
D'où la formule ci-dessous :Sum under the marked area = Sum(OB) - Sum(OD) - Sum(OA) + Sum(OC) The above formula gets reduced to Query(x1y1x2y2) = getSum(x2 y2) - getSum(x2 y1-1) - getSum(x1-1 y2) + getSum(x1-1 y1-1)où
x1 y1 = coordonnées x et y de C
x2 y2 = coordonnées x et y de B
La fonction updateBIT(x y val) met à jour tous les éléments de la région – (x y) vers (N M) où
N = coordonnée X maximale de toute la matrice.
M = coordonnée Y maximale de toute la matrice.
La procédure de repos est assez similaire à celle de l'arbre indexé binaire 1D.Vous trouverez ci-dessous l'implémentation C++ de l'arbre indexé 2D
C++Java/* C++ program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1 <=x2 and y1 <=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. */ #includeusing namespace std ; #define N 4 // N-->max_x and max_y // A structure to hold the queries struct Query { int x1 y1 ; // x and y co-ordinates of bottom left int x2 y2 ; // x and y co-ordinates of top right }; // A function to update the 2D BIT void updateBIT ( int BIT [][ N + 1 ] int x int y int val ) { for (; x <= N ; x += ( x & - x )) { // This loop update all the 1D BIT inside the // array of 1D BIT = BIT[x] for ( int yy = y ; yy <= N ; yy += ( yy & - yy )) BIT [ x ][ yy ] += val ; } return ; } // A function to get sum from (0 0) to (x y) int getSum ( int BIT [][ N + 1 ] int x int y ) { int sum = 0 ; for (; x > 0 ; x -= x &- x ) { // This loop sum through all the 1D BIT // inside the array of 1D BIT = BIT[x] for ( int yy = y ; yy > 0 ; yy -= yy &- yy ) { sum += BIT [ x ][ yy ]; } } return sum ; } // A function to create an auxiliary matrix // from the given input matrix void constructAux ( int mat [][ N ] int aux [][ N + 1 ]) { // Initialise Auxiliary array to 0 for ( int i = 0 ; i <= N ; i ++ ) for ( int j = 0 ; j <= N ; j ++ ) aux [ i ][ j ] = 0 ; // Construct the Auxiliary Matrix for ( int j = 1 ; j <= N ; j ++ ) for ( int i = 1 ; i <= N ; i ++ ) aux [ i ][ j ] = mat [ N - j ][ i -1 ]; return ; } // A function to construct a 2D BIT void construct2DBIT ( int mat [][ N ] int BIT [][ N + 1 ]) { // Create an auxiliary matrix int aux [ N + 1 ][ N + 1 ]; constructAux ( mat aux ); // Initialise the BIT to 0 for ( int i = 1 ; i <= N ; i ++ ) for ( int j = 1 ; j <= N ; j ++ ) BIT [ i ][ j ] = 0 ; for ( int j = 1 ; j <= N ; j ++ ) { for ( int i = 1 ; i <= N ; i ++ ) { // Creating a 2D-BIT using update function // everytime we/ encounter a value in the // input 2D-array int v1 = getSum ( BIT i j ); int v2 = getSum ( BIT i j -1 ); int v3 = getSum ( BIT i -1 j -1 ); int v4 = getSum ( BIT i -1 j ); // Assigning a value to a particular element // of 2D BIT updateBIT ( BIT i j aux [ i ][ j ] - ( v1 - v2 - v4 + v3 )); } } return ; } // A function to answer the queries void answerQueries ( Query q [] int m int BIT [][ N + 1 ]) { for ( int i = 0 ; i < m ; i ++ ) { int x1 = q [ i ]. x1 + 1 ; int y1 = q [ i ]. y1 + 1 ; int x2 = q [ i ]. x2 + 1 ; int y2 = q [ i ]. y2 + 1 ; int ans = getSum ( BIT x2 y2 ) - getSum ( BIT x2 y1 -1 ) - getSum ( BIT x1 -1 y2 ) + getSum ( BIT x1 -1 y1 -1 ); printf ( 'Query(%d %d %d %d) = %d n ' q [ i ]. x1 q [ i ]. y1 q [ i ]. x2 q [ i ]. y2 ans ); } return ; } // Driver program int main () { int mat [ N ][ N ] = {{ 1 2 3 4 } { 5 3 8 1 } { 4 6 7 5 } { 2 4 8 9 }}; // Create a 2D Binary Indexed Tree int BIT [ N + 1 ][ N + 1 ]; construct2DBIT ( mat BIT ); /* Queries of the form - x1 y1 x2 y2 For example the query- {1 1 3 2} means the sub-matrix- y / 3 | 1 2 3 4 Sub-matrix 2 | 5 3 8 1 {1132} ---> 3 8 1 1 | 4 6 7 5 6 7 5 0 | 2 4 8 9 | --|------ 0 1 2 3 ----> x | Hence sum of the sub-matrix = 3+8+1+6+7+5 = 30 */ Query q [] = {{ 1 1 3 2 } { 2 3 3 3 } { 1 1 1 1 }}; int m = sizeof ( q ) / sizeof ( q [ 0 ]); answerQueries ( q m BIT ); return ( 0 ); } Python3/* Java program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1 <=x2 and y1 <=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. */ class GFG { static final int N = 4 ; // N-.max_x and max_y // A structure to hold the queries static class Query { int x1 y1 ; // x and y co-ordinates of bottom left int x2 y2 ; // x and y co-ordinates of top right public Query ( int x1 int y1 int x2 int y2 ) { this . x1 = x1 ; this . y1 = y1 ; this . x2 = x2 ; this . y2 = y2 ; } }; // A function to update the 2D BIT static void updateBIT ( int BIT [][] int x int y int val ) { for (; x <= N ; x += ( x & - x )) { // This loop update all the 1D BIT inside the // array of 1D BIT = BIT[x] for (; y <= N ; y += ( y & - y )) BIT [ x ][ y ] += val ; } return ; } // A function to get sum from (0 0) to (x y) static int getSum ( int BIT [][] int x int y ) { int sum = 0 ; for (; x > 0 ; x -= x &- x ) { // This loop sum through all the 1D BIT // inside the array of 1D BIT = BIT[x] for (; y > 0 ; y -= y &- y ) { sum += BIT [ x ][ y ] ; } } return sum ; } // A function to create an auxiliary matrix // from the given input matrix static void constructAux ( int mat [][] int aux [][] ) { // Initialise Auxiliary array to 0 for ( int i = 0 ; i <= N ; i ++ ) for ( int j = 0 ; j <= N ; j ++ ) aux [ i ][ j ] = 0 ; // Construct the Auxiliary Matrix for ( int j = 1 ; j <= N ; j ++ ) for ( int i = 1 ; i <= N ; i ++ ) aux [ i ][ j ] = mat [ N - j ][ i - 1 ] ; return ; } // A function to construct a 2D BIT static void construct2DBIT ( int mat [][] int BIT [][] ) { // Create an auxiliary matrix int [][] aux = new int [ N + 1 ][ N + 1 ] ; constructAux ( mat aux ); // Initialise the BIT to 0 for ( int i = 1 ; i <= N ; i ++ ) for ( int j = 1 ; j <= N ; j ++ ) BIT [ i ][ j ] = 0 ; for ( int j = 1 ; j <= N ; j ++ ) { for ( int i = 1 ; i <= N ; i ++ ) { // Creating a 2D-BIT using update function // everytime we/ encounter a value in the // input 2D-array int v1 = getSum ( BIT i j ); int v2 = getSum ( BIT i j - 1 ); int v3 = getSum ( BIT i - 1 j - 1 ); int v4 = getSum ( BIT i - 1 j ); // Assigning a value to a particular element // of 2D BIT updateBIT ( BIT i j aux [ i ][ j ] - ( v1 - v2 - v4 + v3 )); } } return ; } // A function to answer the queries static void answerQueries ( Query q [] int m int BIT [][] ) { for ( int i = 0 ; i < m ; i ++ ) { int x1 = q [ i ] . x1 + 1 ; int y1 = q [ i ] . y1 + 1 ; int x2 = q [ i ] . x2 + 1 ; int y2 = q [ i ] . y2 + 1 ; int ans = getSum ( BIT x2 y2 ) - getSum ( BIT x2 y1 - 1 ) - getSum ( BIT x1 - 1 y2 ) + getSum ( BIT x1 - 1 y1 - 1 ); System . out . printf ( 'Query(%d %d %d %d) = %dn' q [ i ] . x1 q [ i ] . y1 q [ i ] . x2 q [ i ] . y2 ans ); } return ; } // Driver Code public static void main ( String [] args ) { int mat [][] = { { 1 2 3 4 } { 5 3 8 1 } { 4 6 7 5 } { 2 4 8 9 } }; // Create a 2D Binary Indexed Tree int [][] BIT = new int [ N + 1 ][ N + 1 ] ; construct2DBIT ( mat BIT ); /* Queries of the form - x1 y1 x2 y2 For example the query- {1 1 3 2} means the sub-matrix- y / 3 | 1 2 3 4 Sub-matrix 2 | 5 3 8 1 {1132} --. 3 8 1 1 | 4 6 7 5 6 7 5 0 | 2 4 8 9 | --|------ 0 1 2 3 ---. x | Hence sum of the sub-matrix = 3+8+1+6+7+5 = 30 */ Query q [] = { new Query ( 1 1 3 2 ) new Query ( 2 3 3 3 ) new Query ( 1 1 1 1 )}; int m = q . length ; answerQueries ( q m BIT ); } } // This code is contributed by 29AjayKumarC#'''Python3 program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1 <=x2 and y1 <=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. ''' N = 4 # N-.max_x and max_y # A structure to hold the queries class Query : def __init__ ( self x1 y1 x2 y2 ): self . x1 = x1 ; self . y1 = y1 ; self . x2 = x2 ; self . y2 = y2 ; # A function to update the 2D BIT def updateBIT ( BIT x y val ): while x <= N : # This loop update all the 1D BIT inside the # array of 1D BIT = BIT[x] while y <= N : BIT [ x ][ y ] += val ; y += ( y & - y ) x += ( x & - x ) return ; # A function to get sum from (0 0) to (x y) def getSum ( BIT x y ): sum = 0 ; while x > 0 : # This loop sum through all the 1D BIT # inside the array of 1D BIT = BIT[x] while y > 0 : sum += BIT [ x ][ y ]; y -= y &- y x -= x &- x return sum ; # A function to create an auxiliary matrix # from the given input matrix def constructAux ( mat aux ): # Initialise Auxiliary array to 0 for i in range ( N + 1 ): for j in range ( N + 1 ): aux [ i ][ j ] = 0 # Construct the Auxiliary Matrix for j in range ( 1 N + 1 ): for i in range ( 1 N + 1 ): aux [ i ][ j ] = mat [ N - j ][ i - 1 ]; return # A function to construct a 2D BIT def construct2DBIT ( mat BIT ): # Create an auxiliary matrix aux = [ None for i in range ( N + 1 )] for i in range ( N + 1 ) : aux [ i ] = [ None for i in range ( N + 1 )] constructAux ( mat aux ) # Initialise the BIT to 0 for i in range ( 1 N + 1 ): for j in range ( 1 N + 1 ): BIT [ i ][ j ] = 0 ; for j in range ( 1 N + 1 ): for i in range ( 1 N + 1 ): # Creating a 2D-BIT using update function # everytime we/ encounter a value in the # input 2D-array v1 = getSum ( BIT i j ); v2 = getSum ( BIT i j - 1 ); v3 = getSum ( BIT i - 1 j - 1 ); v4 = getSum ( BIT i - 1 j ); # Assigning a value to a particular element # of 2D BIT updateBIT ( BIT i j aux [ i ][ j ] - ( v1 - v2 - v4 + v3 )); return ; # A function to answer the queries def answerQueries ( q m BIT ): for i in range ( m ): x1 = q [ i ] . x1 + 1 ; y1 = q [ i ] . y1 + 1 ; x2 = q [ i ] . x2 + 1 ; y2 = q [ i ] . y2 + 1 ; ans = getSum ( BIT x2 y2 ) - getSum ( BIT x2 y1 - 1 ) - getSum ( BIT x1 - 1 y2 ) + getSum ( BIT x1 - 1 y1 - 1 ); print ( 'Query (' q [ i ] . x1 ' ' q [ i ] . y1 ' ' q [ i ] . x2 ' ' q [ i ] . y2 ') = ' ans sep = '' ) return ; # Driver Code mat = [[ 1 2 3 4 ] [ 5 3 8 1 ] [ 4 6 7 5 ] [ 2 4 8 9 ]]; # Create a 2D Binary Indexed Tree BIT = [ None for i in range ( N + 1 )] for i in range ( N + 1 ): BIT [ i ] = [ None for i in range ( N + 1 )] for j in range ( N + 1 ): BIT [ i ][ j ] = 0 construct2DBIT ( mat BIT ); ''' Queries of the form - x1 y1 x2 y2 For example the query- {1 1 3 2} means the sub-matrix- y / 3 | 1 2 3 4 Sub-matrix 2 | 5 3 8 1 {1132} --. 3 8 1 1 | 4 6 7 5 6 7 5 0 | 2 4 8 9 | --|------ 0 1 2 3 ---. x | Hence sum of the sub-matrix = 3+8+1+6+7+5 = 30 ''' q = [ Query ( 1 1 3 2 ) Query ( 2 3 3 3 ) Query ( 1 1 1 1 )]; m = len ( q ) answerQueries ( q m BIT ); # This code is contributed by phasing17JavaScript/* C# program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by.Adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and.Adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1 <=x2 and y1 <=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. */ using System ; class GFG { static readonly int N = 4 ; // N-.max_x and max_y // A structure to hold the queries public class Query { public int x1 y1 ; // x and y co-ordinates of bottom left public int x2 y2 ; // x and y co-ordinates of top right public Query ( int x1 int y1 int x2 int y2 ) { this . x1 = x1 ; this . y1 = y1 ; this . x2 = x2 ; this . y2 = y2 ; } }; // A function to update the 2D BIT static void updateBIT ( int [] BIT int x int y int val ) { for (; x <= N ; x += ( x & - x )) { // This loop update all the 1D BIT inside the // array of 1D BIT = BIT[x] for (; y <= N ; y += ( y & - y )) BIT [ x y ] += val ; } return ; } // A function to get sum from (0 0) to (x y) static int getSum ( int [] BIT int x int y ) { int sum = 0 ; for (; x > 0 ; x -= x &- x ) { // This loop sum through all the 1D BIT // inside the array of 1D BIT = BIT[x] for (; y > 0 ; y -= y &- y ) { sum += BIT [ x y ]; } } return sum ; } // A function to create an auxiliary matrix // from the given input matrix static void constructAux ( int [] mat int [] aux ) { // Initialise Auxiliary array to 0 for ( int i = 0 ; i <= N ; i ++ ) for ( int j = 0 ; j <= N ; j ++ ) aux [ i j ] = 0 ; // Construct the Auxiliary Matrix for ( int j = 1 ; j <= N ; j ++ ) for ( int i = 1 ; i <= N ; i ++ ) aux [ i j ] = mat [ N - j i - 1 ]; return ; } // A function to construct a 2D BIT static void construct2DBIT ( int [] mat int [] BIT ) { // Create an auxiliary matrix int [] aux = new int [ N + 1 N + 1 ]; constructAux ( mat aux ); // Initialise the BIT to 0 for ( int i = 1 ; i <= N ; i ++ ) for ( int j = 1 ; j <= N ; j ++ ) BIT [ i j ] = 0 ; for ( int j = 1 ; j <= N ; j ++ ) { for ( int i = 1 ; i <= N ; i ++ ) { // Creating a 2D-BIT using update function // everytime we/ encounter a value in the // input 2D-array int v1 = getSum ( BIT i j ); int v2 = getSum ( BIT i j - 1 ); int v3 = getSum ( BIT i - 1 j - 1 ); int v4 = getSum ( BIT i - 1 j ); // Assigning a value to a particular element // of 2D BIT updateBIT ( BIT i j aux [ i j ] - ( v1 - v2 - v4 + v3 )); } } return ; } // A function to answer the queries static void answerQueries ( Query [] q int m int [] BIT ) { for ( int i = 0 ; i < m ; i ++ ) { int x1 = q [ i ]. x1 + 1 ; int y1 = q [ i ]. y1 + 1 ; int x2 = q [ i ]. x2 + 1 ; int y2 = q [ i ]. y2 + 1 ; int ans = getSum ( BIT x2 y2 ) - getSum ( BIT x2 y1 - 1 ) - getSum ( BIT x1 - 1 y2 ) + getSum ( BIT x1 - 1 y1 - 1 ); Console . Write ( 'Query({0} {1} {2} {3}) = {4}n' q [ i ]. x1 q [ i ]. y1 q [ i ]. x2 q [ i ]. y2 ans ); } return ; } // Driver Code public static void Main ( String [] args ) { int [] mat = { { 1 2 3 4 } { 5 3 8 1 } { 4 6 7 5 } { 2 4 8 9 } }; // Create a 2D Binary Indexed Tree int [] BIT = new int [ N + 1 N + 1 ]; construct2DBIT ( mat BIT ); /* Queries of the form - x1 y1 x2 y2 For example the query- {1 1 3 2} means the sub-matrix- y / 3 | 1 2 3 4 Sub-matrix 2 | 5 3 8 1 {1132} --. 3 8 1 1 | 4 6 7 5 6 7 5 0 | 2 4 8 9 | --|------ 0 1 2 3 ---. x | Hence sum of the sub-matrix = 3+8+1+6+7+5 = 30 */ Query [] q = { new Query ( 1 1 3 2 ) new Query ( 2 3 3 3 ) new Query ( 1 1 1 1 )}; int m = q . Length ; answerQueries ( q m BIT ); } } // This code is contributed by Rajput-Ji
' ); } return ; } // Driver Code let mat = [[ 1 2 3 4 ] [ 5 3 8 1 ] [ 4 6 7 5 ] [ 2 4 8 9 ]]; // Create a 2D Binary Indexed Tree let BIT = new Array ( N + 1 ); for ( let i = 0 ; i < ( N + 1 ); i ++ ) { BIT [ i ] = new Array ( N + 1 ); for ( let j = 0 ; j < ( N + 1 ); j ++ ) { BIT [ i ][ j ] = 0 ; } } construct2DBIT ( mat BIT ); /* Queries of the form - x1 y1 x2 y2 For example the query- {1 1 3 2} means the sub-matrix- y / 3 | 1 2 3 4 Sub-matrix 2 | 5 3 8 1 {1132} --. 3 8 1 1 | 4 6 7 5 6 7 5 0 | 2 4 8 9 | --|------ 0 1 2 3 ---. x | Hence sum of the sub-matrix = 3+8+1+6+7+5 = 30 */ let q = [ new Query ( 1 1 3 2 ) new Query ( 2 3 3 3 ) new Query ( 1 1 1 1 )]; let m = q . length ; answerQueries ( q m BIT ); // This code is contributed by rag2127 < /script>
SortirQuery(1 1 3 2) = 30 Query(2 3 3 3) = 7 Query(1 1 1 1) = 6Complexité temporelle :
- La fonction updateBIT(x y val) et la fonction getSum(x y) prennent du temps O(log(N)*log(M)).
- Construire le BIT 2D prend O(NM log(N)*log(M)).
- Puisque dans chacune des requêtes nous appelons la fonction getSum(x y), il faut donc répondre à toutes les requêtes Q O(Q*log(N)*log(M)) temps.
- Par conséquent, la complexité temporelle globale du programme est O((NM+Q)*log(N)*log(M)) où
N = coordonnée X maximale de toute la matrice.
M = coordonnée Y maximale de toute la matrice.
Q = Nombre de requêtes.
Espace auxiliaire : O(NM) pour stocker le BIT et le tableau auxiliaire