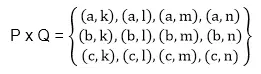Kara mayınlarının olduğu bir yolda en kısa güvenli rotayı bulun
Dikdörtgensel bir matris verildiğinde mat[][] Bazı hücrelerin mayın içerdiği (0 ile gösterilir) ve geri kalanların güvenli olduğu (1 ile gösterilir) durumda, ilk sütundaki herhangi bir hücreden son sütundaki herhangi bir hücreye giden en kısa güvenli rotanın uzunluğunu bulun.
- Kara mayınları güvensizdir ve bitişik dört hücresi (yukarı, sol, sağ) da güvensizdir.
- Bitişik güvenli hücrelere yalnızca yatay ve dikey hareketlere izin verilir.
- Son sütuna güvenli bir şekilde ulaşmak mümkün değilse -1 değerini döndürün.
Örnekler:
Giriş:
ile[][] = [ [1 0 1 1 1]
[1 1 1 1 1]
[1 1 1 1 1]
[1 1 1 0 1]
[1 1 1 1 0] ]
Çıkış: 6
Açıklama: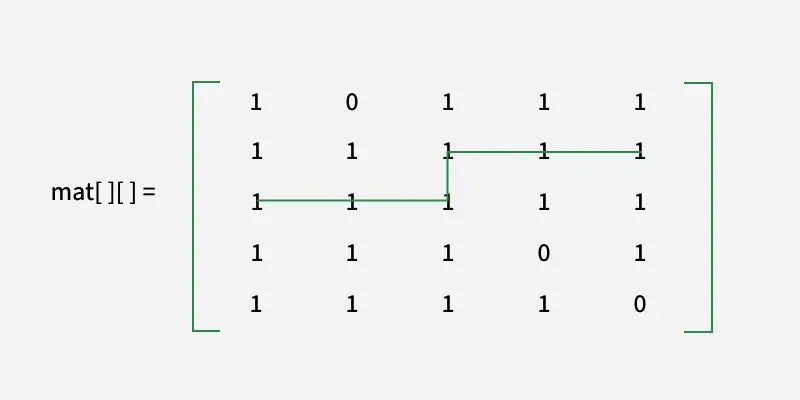
En kısa uzunluğu görebiliriz
Güvenli yol 6'dır.
Giriş:
ile[][] = [ [1 1 1 1 1]
[1 1 0 1 1]
[1 1 1 1 1] ]
Çıkış: -1
Açıklama: Buradan olası bir yol yok
ilk sütundan son sütuna.
İçerik Tablosu
[Yaklaşım] Geri İzlemeyi Kullanma
C++Fikir kullanmaktır Geri izleme . Öncelikle kara mayınlarının tüm bitişik hücrelerini güvensiz olarak işaretliyoruz. Daha sonra matrisin ilk sütunundaki her güvenli hücre için izin verilen tüm yönlerde ilerliyoruz ve yinelemeli olarak bunların hedefe ulaşıp ulaşmadığını kontrol ediyoruz. Hedef bulunursa en kısa yolun değerini güncelleriz, aksi takdirde yukarıdaki çözümlerin hiçbiri işe yaramazsa işlevimizden false değerini döndürürüz.
#include #include #include #include using namespace std ; // Function to mark unsafe cells (landmines and their adjacent cells) void markUnsafeCells ( vector < vector < int >> & mat ) { int r = mat . size (); int c = mat [ 0 ]. size (); // Directions for adjacent cells: up down left right int row [] = { -1 1 0 0 }; int col [] = { 0 0 -1 1 }; vector < vector < int >> temp = mat ; // Mark adjacent cells of landmines (0) as unsafe (0) for ( int i = 0 ; i < r ; i ++ ) { for ( int j = 0 ; j < c ; j ++ ) { if ( temp [ i ][ j ] == 0 ) { for ( int k = 0 ; k < 4 ; k ++ ) { int ni = i + row [ k ]; int nj = j + col [ k ]; if ( ni >= 0 && ni < r && nj >= 0 && nj < c ) { mat [ ni ][ nj ] = 0 ; } } } } } } // DFS to find shortest path from (i j) to any cell in last column int dfs ( vector < vector < int >> & mat vector < vector < bool >> & visited int i int j int c ) { int r = mat . size (); if ( i < 0 || i >= r || j < 0 || j >= c || mat [ i ][ j ] == 0 || visited [ i ][ j ]) { return INT_MAX ; } if ( j == c - 1 ) { return 1 ; } visited [ i ][ j ] = true ; // Four possible moves: up down left right int row [] = { -1 1 0 0 }; int col [] = { 0 0 -1 1 }; int minPath = INT_MAX ; // Try all four directions for ( int k = 0 ; k < 4 ; k ++ ) { int ni = i + row [ k ]; int nj = j + col [ k ]; int pathLength = dfs ( mat visited ni nj c ); if ( pathLength != INT_MAX ) { minPath = min ( minPath 1 + pathLength ); } } // Backtrack - unmark current cell visited [ i ][ j ] = false ; return minPath ; } int findShortestPath ( vector < vector < int >> & mat ) { int r = mat . size (); int c = mat [ 0 ]. size (); // Mark all adjacent cells of landmines as unsafe markUnsafeCells ( mat ); // Initialize visited array vector < vector < bool >> visited ( r vector < bool > ( c false )); int minPath = INT_MAX ; // Try starting from each safe cell in the first column for ( int i = 0 ; i < r ; i ++ ) { if ( mat [ i ][ 0 ] == 1 ) { int pathLength = dfs ( mat visited i 0 c ); if ( pathLength != INT_MAX ) { minPath = min ( minPath pathLength ); } } } return minPath == INT_MAX ? -1 : minPath ; } int main () { vector < vector < int >> mat = { { 1 0 1 1 1 } { 1 1 1 1 1 } { 1 1 1 1 1 } { 1 1 1 0 1 } { 1 1 1 1 0 } }; int result = findShortestPath ( mat ); cout < < result < < endl ; return 0 ; }
Java import java.util.Arrays ; class Solution { // Function to mark unsafe cells (landmines and their adjacent cells) private void markUnsafeCells ( int [][] mat ) { int r = mat . length ; int c = mat [ 0 ] . length ; int [] row = { - 1 1 0 0 }; int [] col = { 0 0 - 1 1 }; // Create a copy to avoid modifying original safe cells prematurely int [][] temp = new int [ r ][ c ] ; for ( int i = 0 ; i < r ; i ++ ) { for ( int j = 0 ; j < c ; j ++ ) { temp [ i ][ j ] = mat [ i ][ j ] ; } } // Mark adjacent cells of landmines (0) as unsafe (0) for ( int i = 0 ; i < r ; i ++ ) { for ( int j = 0 ; j < c ; j ++ ) { if ( temp [ i ][ j ] == 0 ) { for ( int k = 0 ; k < 4 ; k ++ ) { int ni = i + row [ k ] ; int nj = j + col [ k ] ; if ( ni >= 0 && ni < r && nj >= 0 && nj < c ) { mat [ ni ][ nj ] = 0 ; } } } } } } // DFS to find shortest path from (i j) to any cell in last column private int dfs ( int [][] mat boolean [][] visited int i int j int c ) { int r = mat . length ; // If out of bounds blocked or visited if ( i < 0 || i >= r || j < 0 || j >= c || mat [ i ][ j ] == 0 || visited [ i ][ j ] ) { return Integer . MAX_VALUE ; } if ( j == c - 1 ) { return 1 ; } visited [ i ][ j ] = true ; int [] row = { - 1 1 0 0 }; int [] col = { 0 0 - 1 1 }; int minPath = Integer . MAX_VALUE ; // Try all four directions for ( int k = 0 ; k < 4 ; k ++ ) { int ni = i + row [ k ] ; int nj = j + col [ k ] ; int pathLength = dfs ( mat visited ni nj c ); if ( pathLength != Integer . MAX_VALUE ) { minPath = Math . min ( minPath 1 + pathLength ); } } // Backtrack - unmark current cell visited [ i ][ j ] = false ; return minPath ; } public int findShortestPath ( int [][] mat ) { int r = mat . length ; int c = mat [ 0 ] . length ; // Mark all adjacent cells of landmines as unsafe markUnsafeCells ( mat ); boolean [][] visited = new boolean [ r ][ c ] ; int minPath = Integer . MAX_VALUE ; // Try starting from each safe cell in the first column for ( int i = 0 ; i < r ; i ++ ) { if ( mat [ i ][ 0 ] == 1 ) { int pathLength = dfs ( mat visited i 0 c ); if ( pathLength != Integer . MAX_VALUE ) { minPath = Math . min ( minPath pathLength ); } } } return minPath == Integer . MAX_VALUE ? - 1 : minPath ; } public static void main ( String [] args ) { int [][] mat = { { 1 0 1 1 1 } { 1 1 1 1 1 } { 1 1 1 1 1 } { 1 1 1 0 1 } { 1 1 1 1 0 } }; Solution solution = new Solution (); int result = solution . findShortestPath ( mat ); System . out . println ( result ); } }
Python # Function to mark unsafe cells (landmines and their adjacent cells) def mark_unsafe_cells ( mat ): r = len ( mat ) c = len ( mat [ 0 ]) # Directions for adjacent cells: up down left right row = [ - 1 1 0 0 ] col = [ 0 0 - 1 1 ] # Create a copy to avoid modifying original safe cells prematurely temp = [ row [:] for row in mat ] # Mark adjacent cells of landmines (0) as unsafe (0) for i in range ( r ): for j in range ( c ): if temp [ i ][ j ] == 0 : for k in range ( 4 ): ni = i + row [ k ] nj = j + col [ k ] if 0 <= ni < r and 0 <= nj < c : mat [ ni ][ nj ] = 0 # DFS to find shortest path from (i j) to any cell in last column def dfs ( mat visited i j c ): r = len ( mat ) # If out of bounds blocked or visited if i < 0 or i >= r or j < 0 or j >= c or mat [ i ][ j ] == 0 or visited [ i ][ j ]: return float ( 'inf' ) if j == c - 1 : return 1 visited [ i ][ j ] = True # Four possible moves: up down left right row = [ - 1 1 0 0 ] col = [ 0 0 - 1 1 ] min_path = float ( 'inf' ) # Try all four directions for k in range ( 4 ): ni = i + row [ k ] nj = j + col [ k ] path_length = dfs ( mat visited ni nj c ) if path_length != float ( 'inf' ): min_path = min ( min_path 1 + path_length ) # Backtrack - unmark current cell visited [ i ][ j ] = False return min_path def findShortestPath ( mat ): r = len ( mat ) c = len ( mat [ 0 ]) # Mark all adjacent cells of landmines as unsafe mark_unsafe_cells ( mat ) visited = [[ False ] * c for _ in range ( r )] min_path = float ( 'inf' ) # Try starting from each safe cell in the first column for i in range ( r ): if mat [ i ][ 0 ] == 1 : path_length = dfs ( mat visited i 0 c ) if path_length != float ( 'inf' ): min_path = min ( min_path path_length ) return - 1 if min_path == float ( 'inf' ) else min_path def main (): mat = [ [ 1 0 1 1 1 ] [ 1 1 1 1 1 ] [ 1 1 1 1 1 ] [ 1 1 1 0 1 ] [ 1 1 1 1 0 ] ] result = findShortestPath ( mat ) print ( result ) if __name__ == '__main__' : main ()
C# using System ; class GFG { // Function to mark unsafe cells (landmines and their adjacent cells) private void MarkUnsafeCells ( int [][] mat ) { int r = mat . Length ; int c = mat [ 0 ]. Length ; // Directions for adjacent cells: up down left right int [] row = { - 1 1 0 0 }; int [] col = { 0 0 - 1 1 }; // Create a copy to avoid modifying original safe cells prematurely int [][] temp = new int [ r ][]; for ( int i = 0 ; i < r ; i ++ ) { temp [ i ] = new int [ c ]; Array . Copy ( mat [ i ] temp [ i ] c ); } // Mark adjacent cells of landmines (0) as unsafe (0) for ( int i = 0 ; i < r ; i ++ ) { for ( int j = 0 ; j < c ; j ++ ) { if ( temp [ i ][ j ] == 0 ) { for ( int k = 0 ; k < 4 ; k ++ ) { int ni = i + row [ k ]; int nj = j + col [ k ]; if ( ni >= 0 && ni < r && nj >= 0 && nj < c ) { mat [ ni ][ nj ] = 0 ; } } } } } } // DFS to find shortest path from (i j) to any cell in last column private int Dfs ( int [][] mat bool [][] visited int i int j int c ) { int r = mat . Length ; // If out of bounds blocked or visited if ( i < 0 || i >= r || j < 0 || j >= c || mat [ i ][ j ] == 0 || visited [ i ][ j ]) { return int . MaxValue ; } if ( j == c - 1 ) { return 1 ; } visited [ i ][ j ] = true ; int [] row = { - 1 1 0 0 }; int [] col = { 0 0 - 1 1 }; int minPath = int . MaxValue ; // Try all four directions for ( int k = 0 ; k < 4 ; k ++ ) { int ni = i + row [ k ]; int nj = j + col [ k ]; int pathLength = Dfs ( mat visited ni nj c ); if ( pathLength != int . MaxValue ) { minPath = Math . Min ( minPath 1 + pathLength ); } } // Backtrack - unmark current cell visited [ i ][ j ] = false ; return minPath ; } public int FindShortestPath ( int [][] mat ) { int r = mat . Length ; int c = mat [ 0 ]. Length ; // Mark all adjacent cells of landmines as unsafe MarkUnsafeCells ( mat ); bool [][] visited = new bool [ r ][]; for ( int i = 0 ; i < r ; i ++ ) { visited [ i ] = new bool [ c ]; } int minPath = int . MaxValue ; // Try starting from each safe cell in the first column for ( int i = 0 ; i < r ; i ++ ) { if ( mat [ i ][ 0 ] == 1 ) { int pathLength = Dfs ( mat visited i 0 c ); if ( pathLength != int . MaxValue ) { minPath = Math . Min ( minPath pathLength ); } } } return minPath == int . MaxValue ? - 1 : minPath ; } static void Main ( string [] args ) { int [][] mat = new int [][] { new int [] { 1 0 1 1 1 } new int [] { 1 1 1 1 1 } new int [] { 1 1 1 1 1 } new int [] { 1 1 1 0 1 } new int [] { 1 1 1 1 0 } }; GFG solution = new GFG (); int result = solution . FindShortestPath ( mat ); Console . WriteLine ( result ); } }
JavaScript function markUnsafeCells ( mat ) { const r = mat . length ; const c = mat [ 0 ]. length ; // Directions for adjacent cells: up down left right const row = [ - 1 1 0 0 ]; const col = [ 0 0 - 1 1 ]; // Create a copy to avoid modifying original safe cells prematurely const temp = mat . map ( row => [... row ]); // Mark adjacent cells of landmines (0) as unsafe (0) for ( let i = 0 ; i < r ; i ++ ) { for ( let j = 0 ; j < c ; j ++ ) { if ( temp [ i ][ j ] === 0 ) { for ( let k = 0 ; k < 4 ; k ++ ) { const ni = i + row [ k ]; const nj = j + col [ k ]; if ( ni >= 0 && ni < r && nj >= 0 && nj < c ) { mat [ ni ][ nj ] = 0 ; } } } } } } function dfs ( mat visited i j c ) { const r = mat . length ; // If out of bounds blocked or visited if ( i < 0 || i >= r || j < 0 || j >= c || mat [ i ][ j ] === 0 || visited [ i ][ j ]) { return Infinity ; } // If reached the last column if ( j === c - 1 ) { return 1 ; } visited [ i ][ j ] = true ; const row = [ - 1 1 0 0 ]; const col = [ 0 0 - 1 1 ]; let minPath = Infinity ; // Try all four directions for ( let k = 0 ; k < 4 ; k ++ ) { const ni = i + row [ k ]; const nj = j + col [ k ]; const pathLength = dfs ( mat visited ni nj c ); if ( pathLength !== Infinity ) { minPath = Math . min ( minPath 1 + pathLength ); } } // Backtrack - unmark current cell visited [ i ][ j ] = false ; return minPath ; } function findShortestPath ( mat ) { const r = mat . length ; const c = mat [ 0 ]. length ; // Mark all adjacent cells of landmines as unsafe markUnsafeCells ( mat ); const visited = Array ( r ). fill (). map (() => Array ( c ). fill ( false )); let minPath = Infinity ; // Try starting from each safe cell in the first column for ( let i = 0 ; i < r ; i ++ ) { if ( mat [ i ][ 0 ] === 1 ) { const pathLength = dfs ( mat visited i 0 c ); if ( pathLength !== Infinity ) { minPath = Math . min ( minPath pathLength ); } } } return minPath === Infinity ? - 1 : minPath ; } const mat = [ [ 1 0 1 1 1 ] [ 1 1 1 1 1 ] [ 1 1 1 1 1 ] [ 1 1 1 0 1 ] [ 1 1 1 1 0 ] ]; const result = findShortestPath ( mat ); console . log ( result );
Çıkış
6
Zaman Karmaşıklığı: O(4^(r * c)) burada r, verilen matristeki satır sayısı ve c, sütun sayısıdır.
Yardımcı Alan: O(r * c) visted[r][c] gibi ekstra alan kullandığımız için.
[Optimize Yaklaşım] Genişlik Öncelikli Aramayı Kullanma
C++Genişlik-Önce Arama kullanılarak polinom zamanda çözülebilir. Son sütundaki tüm güvenli hücreleri mesafe = 1 olacak şekilde kuyruğa alın. BFS ilerledikçe son sütundan her hücreye giden en kısa yol hesaplanır. Son olarak, ilk sütundaki ulaşılabilir tüm hücreler arasında minimum mesafe çıktısı alınır.
#include #include #include #include #include #include using namespace std ; int rowNum [ 4 ] = { -1 0 0 1 }; int colNum [ 4 ] = { 0 -1 1 0 }; int findShortestPath ( vector < vector < int >> & mat ) { int n = mat . size (); int m = mat [ 0 ]. size (); queue < array < int 3 >> q ; // Queue to perform BFS int d [ n ][ m ]; for ( int i = 0 ; i < n ; i ++ ) for ( int j = 0 ; j < m ; j ++ ) d [ i ][ j ] = 1e9 ; // Lambda function to check if cell is valid auto isValid = [ & ]( int i int j ) { if ( i < 0 || i >= n || j < 0 || j >= m ) return false ; return true ; }; // Lambda function to check if cell and its adjacent cells are safe auto check = [ & ]( int i int j ) { if ( ! isValid ( i j )) return false ; for ( int k = 0 ; k < 4 ; k ++ ) { if ( isValid ( i + rowNum [ k ] j + colNum [ k ]) && ! mat [ i + rowNum [ k ]][ j + colNum [ k ]]) return false ; } return true ; }; // Pushing cells from the rightmost column into the queue for ( int i = 0 ; i < n ; i ++ ) { if ( check ( i m - 1 )) { q . push ({ i m - 1 1 }); } } // BFS traversal while ( ! q . empty ()) { auto z = q . front (); int x = z [ 0 ] y = z [ 1 ] dis = z [ 2 ]; q . pop (); if ( d [ x ][ y ] > dis ) { d [ x ][ y ] = dis ; for ( int k = 0 ; k < 4 ; k ++ ) { if ( check ( x + rowNum [ k ] y + colNum [ k ])) { q . push ({ x + rowNum [ k ] y + colNum [ k ] dis + 1 }); } } } } // Finding the minimum distance in the first column int ans = 1e9 ; for ( int i = 0 ; i < n ; i ++ ) ans = min ( ans d [ i ][ 0 ]); // If no safe path found return -1 if ( ans >= 1e9 ) ans = -1 ; return ans ; } int main () { vector < vector < int >> mat = { { 1 0 1 1 1 } { 1 1 1 1 1 } { 1 1 1 1 1 } { 1 1 1 0 1 } { 1 1 1 1 0 } }; int result = findShortestPath ( mat ); cout < < result < < endl ; return 0 ; }
Java import java.util.* ; public class Solution { static int [] rowNum = { - 1 0 0 1 }; static int [] colNum = { 0 - 1 1 0 }; public static int findShortestPath ( int [][] mat ) { int n = mat . length ; int m = mat [ 0 ] . length ; Queue < int []> q = new LinkedList <> (); int [][] d = new int [ n ][ m ] ; // Initializing distance array with large values for ( int i = 0 ; i < n ; i ++ ) { Arrays . fill ( d [ i ] ( int ) 1e9 ); } // Lambda-like helper function: check if cell is valid java . util . function . BiFunction < Integer Integer Boolean > isValid = ( i j ) -> { return ! ( i < 0 || i >= n || j < 0 || j >= m ); }; // Helper function: check if cell and adjacent cells are safe java . util . function . BiFunction < Integer Integer Boolean > check = ( i j ) -> { if ( ! isValid . apply ( i j )) return false ; for ( int k = 0 ; k < 4 ; k ++ ) { int ni = i + rowNum [ k ] ; int nj = j + colNum [ k ] ; if ( isValid . apply ( ni nj ) && mat [ ni ][ nj ] == 0 ) return false ; } return true ; }; // Pushing cells from the rightmost column into the queue for ( int i = 0 ; i < n ; i ++ ) { if ( check . apply ( i m - 1 )) { q . add ( new int [] { i m - 1 1 }); } } // BFS traversal while ( ! q . isEmpty ()) { int [] z = q . poll (); int x = z [ 0 ] y = z [ 1 ] dis = z [ 2 ] ; if ( d [ x ][ y ] > dis ) { d [ x ][ y ] = dis ; for ( int k = 0 ; k < 4 ; k ++ ) { int ni = x + rowNum [ k ] ; int nj = y + colNum [ k ] ; if ( check . apply ( ni nj )) { q . add ( new int [] { ni nj dis + 1 }); } } } } // Finding the minimum distance in the first column int ans = ( int ) 1e9 ; for ( int i = 0 ; i < n ; i ++ ) { ans = Math . min ( ans d [ i ][ 0 ] ); } // If no safe path found return -1 if ( ans >= 1e9 ) ans = - 1 ; return ans ; } public static void main ( String [] args ) { int [][] mat = { { 1 0 1 1 1 } { 1 1 1 1 1 } { 1 1 1 1 1 } { 1 1 1 0 1 } { 1 1 1 1 0 } }; int result = findShortestPath ( mat ); System . out . println ( result ); } }
Python from collections import deque rowNum = [ - 1 0 0 1 ] colNum = [ 0 - 1 1 0 ] def findShortestPath ( mat ): n = len ( mat ) m = len ( mat [ 0 ]) q = deque () d = [[ 10 ** 9 for _ in range ( m )] for _ in range ( n )] # Check if cell is valid def isValid ( i j ): return not ( i < 0 or i >= n or j < 0 or j >= m ) # Check if cell and its adjacent cells are safe def check ( i j ): if not isValid ( i j ): return False for k in range ( 4 ): ni nj = i + rowNum [ k ] j + colNum [ k ] if isValid ( ni nj ) and mat [ ni ][ nj ] == 0 : return False return True # Pushing cells from the rightmost column into the queue for i in range ( n ): if check ( i m - 1 ): q . append (( i m - 1 1 )) # BFS traversal while q : x y dis = q . popleft () if d [ x ][ y ] > dis : d [ x ][ y ] = dis for k in range ( 4 ): ni nj = x + rowNum [ k ] y + colNum [ k ] if check ( ni nj ): q . append (( ni nj dis + 1 )) # Finding the minimum distance in the first column ans = min ( d [ i ][ 0 ] for i in range ( n )) # If no safe path found return -1 if ans >= 10 ** 9 : ans = - 1 return ans if __name__ == '__main__' : mat = [ [ 1 0 1 1 1 ] [ 1 1 1 1 1 ] [ 1 1 1 1 1 ] [ 1 1 1 0 1 ] [ 1 1 1 1 0 ] ] result = findShortestPath ( mat ) print ( result )
C# using System ; using System.Collections.Generic ; class Solution { static int [] rowNum = { - 1 0 0 1 }; static int [] colNum = { 0 - 1 1 0 }; // Check if cell is valid static bool IsValid ( int i int j int n int m ) { return ! ( i < 0 || i >= n || j < 0 || j >= m ); } // Check if cell and its adjacent cells are safe static bool Check ( int i int j int [][] mat int n int m ) { if ( ! IsValid ( i j n m )) return false ; for ( int k = 0 ; k < 4 ; k ++ ) { int ni = i + rowNum [ k ]; int nj = j + colNum [ k ]; if ( IsValid ( ni nj n m ) && mat [ ni ][ nj ] == 0 ) return false ; } return true ; } public static int FindShortestPath ( int [][] mat ) { int n = mat . Length ; int m = mat [ 0 ]. Length ; Queue < ( int int int ) > q = new Queue < ( int int int ) > (); int [] d = new int [ n m ]; // Initialize distance array with large value for ( int i = 0 ; i < n ; i ++ ) for ( int j = 0 ; j < m ; j ++ ) d [ i j ] = int . MaxValue / 2 ; // Push safe cells from rightmost column for ( int i = 0 ; i < n ; i ++ ) { if ( Check ( i m - 1 mat n m )) { q . Enqueue (( i m - 1 1 )); } } // BFS traversal while ( q . Count > 0 ) { var ( x y dis ) = q . Dequeue (); if ( d [ x y ] > dis ) { d [ x y ] = dis ; for ( int k = 0 ; k < 4 ; k ++ ) { int ni = x + rowNum [ k ]; int nj = y + colNum [ k ]; if ( Check ( ni nj mat n m )) { q . Enqueue (( ni nj dis + 1 )); } } } } // Find minimum distance in the first column int ans = int . MaxValue / 2 ; for ( int i = 0 ; i < n ; i ++ ) ans = Math . Min ( ans d [ i 0 ]); return ans >= int . MaxValue / 2 ? - 1 : ans ; } static void Main () { int [][] mat = new int [][] { new int [] { 1 0 1 1 1 } new int [] { 1 1 1 1 1 } new int [] { 1 1 1 1 1 } new int [] { 1 1 1 0 1 } new int [] { 1 1 1 1 0 } }; int result = FindShortestPath ( mat ); Console . WriteLine ( result ); } }
JavaScript function findShortestPath ( mat ) { const n = mat . length ; const m = mat [ 0 ]. length ; const rowNum = [ - 1 0 0 1 ]; const colNum = [ 0 - 1 1 0 ]; // Distance matrix initialized to large value const d = Array . from ({ length : n } () => Array ( m ). fill ( Number . MAX_SAFE_INTEGER )); // Check if cell is valid function isValid ( i j ) { return ! ( i < 0 || i >= n || j < 0 || j >= m ); } // Check if cell and its adjacent cells are safe function check ( i j ) { if ( ! isValid ( i j )) return false ; for ( let k = 0 ; k < 4 ; k ++ ) { let ni = i + rowNum [ k ]; let nj = j + colNum [ k ]; if ( isValid ( ni nj ) && mat [ ni ][ nj ] === 0 ) return false ; } return true ; } // Queue for BFS let q = []; // Push safe cells from rightmost column for ( let i = 0 ; i < n ; i ++ ) { if ( check ( i m - 1 )) { q . push ([ i m - 1 1 ]); } } // BFS traversal while ( q . length > 0 ) { let [ x y dis ] = q . shift (); if ( d [ x ][ y ] > dis ) { d [ x ][ y ] = dis ; for ( let k = 0 ; k < 4 ; k ++ ) { let ni = x + rowNum [ k ]; let nj = y + colNum [ k ]; if ( check ( ni nj )) { q . push ([ ni nj dis + 1 ]); } } } } // Find minimum distance in first column let ans = Number . MAX_SAFE_INTEGER ; for ( let i = 0 ; i < n ; i ++ ) { ans = Math . min ( ans d [ i ][ 0 ]); } return ans >= Number . MAX_SAFE_INTEGER ? - 1 : ans ; } const mat = [ [ 1 0 1 1 1 ] [ 1 1 1 1 1 ] [ 1 1 1 1 1 ] [ 1 1 1 0 1 ] [ 1 1 1 1 0 ] ]; const result = findShortestPath ( mat ); console . log ( result );
Çıkış
6
Zaman Karmaşıklığı: O(r * c) burada r ve c, sırasıyla verilen matristeki satır ve sütun sayısıdır.
Yardımcı Alan: O(r * c)