Söka i binärt sökträd (BST)

Givet a BST , uppgiften är att söka efter en nod i denna BST .
För att söka efter ett värde i BST, betrakta det som en sorterad array. Nu kan vi enkelt utföra sökoperation i BST med hjälp av Binär sökalgoritm .
Algoritm för att söka efter en nyckel i ett givet binärt sökträd:
Låt oss säga att vi vill söka efter numret X, Vi börjar vid roten. Sedan:
- Vi jämför värdet som ska sökas med värdet på roten.
- Om det är lika är vi klara med sökningen om den är mindre, vi vet att vi måste gå till det vänstra underträdet eftersom i ett binärt sökträd är alla element i det vänstra underträdet mindre och alla element i det högra underträdet är större.
- Upprepa steget ovan tills ingen mer korsning är möjlig
- Om nyckel hittas vid någon iteration, returnera True. Annars Falskt.
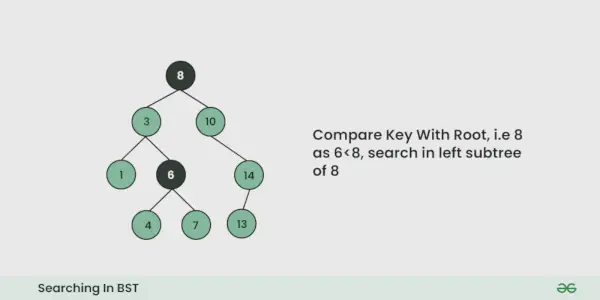
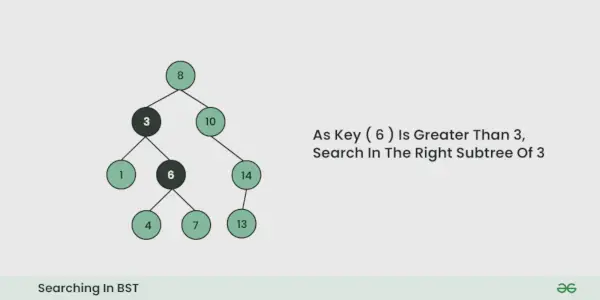
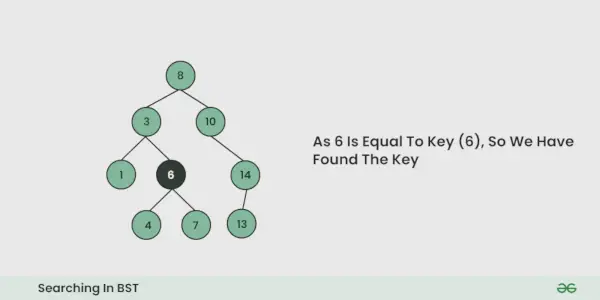
Illustration av sökning i en BST:
Se illustrationen nedan för en bättre förståelse:
Rekommenderad praxisSök en nod i BSTTTry It!

Program för att implementera sökning i BST:
C++
// C++ function to search a given key in a given BST> #include> using> namespace> std;> struct> node {> > int> key;> > struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(> int> item)> {> > struct> node* temp> > => new> struct> node;> > temp->nyckel = objekt;> > temp->vänster = temp->höger = NULL;> > return> temp;> }> // A utility function to insert> // a new node with given key in BST> struct> node* insert(> struct> node* node,> int> key)> {> > // If the tree is empty, return a new node> > if> (node == NULL)> > return> newNode(key);> > // Otherwise, recur down the tree> > if> (key key)> > node->vänster = infoga(nod->vänster, nyckel);> > else> if> (key>nod->nyckel)> > node->höger = infoga(nod->höger, nyckel);> > // Return the (unchanged) node pointer> > return> node;> }> // Utility function to search a key in a BST> struct> node* search(> struct> node* root,> int> key)> > > // Base Cases: root is null or key is present at root> > if> (root == NULL> // Driver Code> int> main()> {> > struct> node* root = NULL;> > root = insert(root, 50);> > insert(root, 30);> > insert(root, 20);> > insert(root, 40);> > insert(root, 70);> > insert(root, 60);> > insert(root, 80);> > // Key to be found> > int> key = 6;> > // Searching in a BST> > if> (search(root, key) == NULL)> > cout < < key < <> ' not found'> < < endl;> > else> > cout < < key < <> ' found'> < < endl;> > key = 60;> > // Searching in a BST> > if> (search(root, key) == NULL)> > cout < < key < <> ' not found'> < < endl;> > else> > cout < < key < <> ' found'> < < endl;> > return> 0;> }> |
C
// C function to search a given key in a given BST> #include> #include> struct> node {> > int> key;> > struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(> int> item)> {> > struct> node* temp> > = (> struct> node*)> malloc> (> sizeof> (> struct> node));> > temp->nyckel = objekt;> > temp->vänster = temp->höger = NULL;> > return> temp;> }> // A utility function to insert> // a new node with given key in BST> struct> node* insert(> struct> node* node,> int> key)> {> > // If the tree is empty, return a new node> > if> (node == NULL)> > return> newNode(key);> > // Otherwise, recur down the tree> > if> (key key)> > node->vänster = infoga(nod->vänster, nyckel);> > else> if> (key>nod->nyckel)> > node->höger = infoga(nod->höger, nyckel);> > // Return the (unchanged) node pointer> > return> node;> }> // Utility function to search a key in a BST> struct> node* search(> struct> node* root,> int> key)> > // Driver Code> int> main()> {> > struct> node* root = NULL;> > root = insert(root, 50);> > insert(root, 30);> > insert(root, 20);> > insert(root, 40);> > insert(root, 70);> > insert(root, 60);> > insert(root, 80);> > // Key to be found> > int> key = 6;> > // Searching in a BST> > if> (search(root, key) == NULL)> > printf> (> '%d not found
'> , key);> > else> > printf> (> '%d found
'> , key);> > key = 60;> > // Searching in a BST> > if> (search(root, key) == NULL)> > printf> (> '%d not found
'> , key);> > else> > printf> (> '%d found
'> , key);> > return> 0;> }> |
Java
// Java program to search a given key in a given BST> class> Node {> > int> key;> > Node left, right;> > public> Node(> int> item) {> > key = item;> > left = right => null> ;> > }> }> class> BinarySearchTree {> > Node root;> > // Constructor> > BinarySearchTree() {> > root => null> ;> > }> > // A utility function to insert> > // a new node with given key in BST> > Node insert(Node node,> int> key) {> > // If the tree is empty, return a new node> > if> (node ==> null> ) {> > node => new> Node(key);> > return> node;> > }> > // Otherwise, recur down the tree> > if> (key node.left = insert(node.left, key); else if (key>node.key) node.right = infoga(nod.höger, nyckel); // Returnera (oförändrad) nodpekarens returnod; } // Verktygsfunktion för att söka efter en nyckel i en BST-nodsökning(Nodrot, int-nyckel) // Driver Code public static void main(String[] args) { BinarySearchTree tree = new BinarySearchTree(); // Infoga noder tree.root = tree.insert(tree.root, 50); tree.insert(tree.root, 30); tree.insert(tree.root, 20); tree.insert(tree.root, 40); tree.insert(tree.root, 70); tree.insert(tree.root, 60); tree.insert(tree.root, 80); // Nyckel som ska hittas int nyckel = 6; // Söker i en BST if (tree.search(tree.root, key) == null) System.out.println(key + ' inte hittat'); else System.out.println(nyckel + ' hittades'); nyckel = 60; // Söker i en BST if (tree.search(tree.root, key) == null) System.out.println(key + ' inte hittat'); else System.out.println(nyckel + ' hittades'); } }> |
Python3
# Python3 function to search a given key in a given BST> class> Node:> > # Constructor to create a new node> > def> __init__(> self> , key):> > self> .key> => key> > self> .left> => None> > self> .right> => None> # A utility function to insert> # a new node with the given key in BST> def> insert(node, key):> > # If the tree is empty, return a new node> > if> node> is> None> :> > return> Node(key)> > # Otherwise, recur down the tree> > if> key node.left = insert(node.left, key) elif key>node.key: node.right = infoga(nod.höger, nyckel) # Returnera (oförändrad) nodpekarens returnod # Verktygsfunktion för att söka efter en nyckel i en BST def-sökning(root, nyckel): # Basfall: roten är null eller nyckel finns vid root om root är None eller root.key == nyckel: returnera root # Key är större än roots nyckel om root.key return search(root.right, key) # Key är mindre än root 's key return search(root.left, key) # Driver Code if __name__ == '__main__': root = Ingen rot = insert(root, 50) insert(root, 30) insert(root, 20) insert (root, 40) insert(root, 70) insert(root, 60) insert(root, 80) # Key to be found key = 6 # Söker i en BST om sök(root, nyckel) är Ingen: print(key, 'not found') else: print(key, 'found') key = 60 # Söker i en BST om sökning (root, key) är Ingen: print(key, 'not found') else: print(nyckel, 'hittad')> |
C#
// C# function to search a given key in a given BST> using> System;> public> class> Node {> > public> int> key;> > public> Node left, right;> }> public> class> BinaryTree {> > // A utility function to create a new BST node> > public> Node NewNode(> int> item)> > {> > Node temp => new> Node();> > temp.key = item;> > temp.left = temp.right => null> ;> > return> temp;> > }> > // A utility function to insert> > // a new node with given key in BST> > public> Node Insert(Node node,> int> key)> > {> > // If the tree is empty, return a new node> > if> (node ==> null> )> > return> NewNode(key);> > // Otherwise, recur down the tree> > if> (key node.left = Insert(node.left, key); else if (key>node.key) node.right = Infoga(nod.höger, nyckel); // Returnera (oförändrad) nodpekarens returnod; } // Verktygsfunktion för att söka efter en nyckel i en BST-publik nodsökning(Nodrot, int-nyckel) // Basfall: root är null eller nyckel finns vid root om (root == null // Driver Code public static void Main () { Node root = null BinaryTree bt = new BinaryTree(); , 40); bt.Insert(root, 70).Insert(root, 80); bt.Search(root, key) == null) Console.WriteLine(nyckel + ' inte hittat'); if (bt.Search(root, key) == null) Console.WriteLine(nyckel + ' inte hittat'); |
>
// Javascript function to search a given key in a given BST>class Node {>>constructor(key) {>>this>.key = key;>>this>.left =>null>;>>this>.right =>null>;>>}>}>// A utility function to insert>// a new node with given key in BST>function>insert(node, key) {>>// If the tree is empty, return a new node>>if>(node ===>null>) {>>return>new>Node(key);>>}>>// Otherwise, recur down the tree>>if>(key node.left = insert(node.left, key); } else if (key>node.key) { node.right = infoga(nod.höger, nyckel); } // Returnera den (oförändrade) nodpekarens returnod; } // Verktygsfunktion för att söka efter en nyckel i en BST-funktionssökning(root, nyckel) { // Basfall: root är null eller nyckel finns vid root om (root === null || root.key === nyckel ) { returnera rot; } // Nyckeln är större än rotens nyckel if (root.key return search(root.right, key); } // Key är mindre än roots nyckel return search(root.left, key); } // Driver Code låt root = insert(root, 30 insert(root, 70); 60); insert(root, 80); // Key to be found let key = 6; // Söker i en BST if (search(root, key) === null) found'); } else { console.log(key + ' found' } key = 60; Söker i en BST if (search(root, key) key + ' inte hittat'); } else { console.log(nyckel + ' found' }>
Produktion
6 not found 60 foundTidskomplexitet: O(h), där h är höjden på BST.
Hjälputrymme: O(h), där h är höjden på BST. Detta beror på att den maximala mängden utrymme som behövs för att lagra rekursionsstacken skulle vara h .Relaterade länkar:
- Binary Search Tree Insert Operation
- Ta bort operation för binärt sökträd