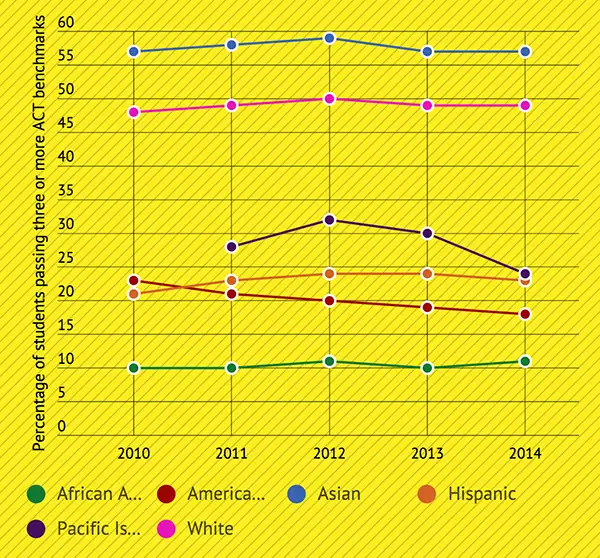
Planar graf:

En graf sägs vara plan om den kan ritas i ett plan så att ingen kant korsar.
Exempel: Grafen som visas i fig är en plan graf.


Region av en graf: Betrakta en plan graf G=(V,E). Ett område definieras som ett område av planet som begränsas av kanter och inte kan delas upp ytterligare. En plan graf delar upp planerna i en eller flera regioner. En av dessa regioner kommer att vara oändlig.
Finita region: Om området i området är ändligt, kallas det området för en ändlig region.
Oändlig region: Om området i området är oändligt kallas det området för ett oändligt område. En plan graf har bara en oändlig region.
Exempel: Betrakta grafen som visas i Fig. Bestäm antalet regioner, ändliga regioner och en oändlig region.

Lösning: Det finns fem regioner i diagrammet ovan, dvs 1 ,r 2 ,r 3 ,r 4 ,r 5 .
Det finns fyra ändliga områden i grafen, dvs r 2 ,r 3 ,r 4 ,r 5 .
Det finns bara en ändlig region, dvs r 1
Egenskaper för plana grafer:
- Om en sammankopplad plan graf G har e kanter och r områden, då r ≦
 Det är.
Det är. - Om en sammankopplad plan graf G har e kanter, v hörn och r områden, då är v-e+r=2.
- Om en ansluten plan graf G har e kanter och v hörn, då 3v-e≧6.
- En komplett graf K n är en plan om och endast om n <5. < li>
- En komplett tvådelad graf K mn är plan om och endast om m3.
Exempel: Bevisa att komplett graf K 4 är plan.
Lösning: Den fullständiga grafen K 4 innehåller 4 hörn och 6 kanter.
Vi vet att för en sammankopplad plan graf 3v-e≧6.Därav för K 4 , vi har 3x4-6=6 som uppfyller fastigheten (3).
Alltså K 4 är en plan graf. Därav bevisat.
Icke-planär graf:
En graf sägs vara icke plan om den inte kan ritas i ett plan så att ingen kant korsar.
Exempel: Graferna som visas i fig är icke plana grafer.

Dessa grafer kan inte ritas i ett plan så att inga kanter korsar, därför är de icke-plana grafer.
Egenskaper för icke-planära grafer:
En graf är icke-plan om och endast om den innehåller en subgraf som är homeomorf till K 5 eller K 3.3
Exempel 1: Visa att K 5 är icke-planär.
Lösning: Den fullständiga grafen K 5 innehåller 5 hörn och 10 kanter.
Nu, för en ansluten plan graf 3v-e≧6.
Därför, för K 5 , vi har 3 x 5-10=5 (vilket inte uppfyller egenskap 3 eftersom det måste vara större än eller lika med 6).
Alltså K 5 är en icke-planär graf.
Exempel 2: Visa att graferna som visas i fig är icke-plana genom att hitta en subgraf som är homeomorf till K 5 eller K 3.3 .


Lösning: Om vi tar bort kanterna (V 1 ,I 4 ),(I 3 ,I 4 ) och (V 5 ,I 4 ) grafen G 1 , blir homeomorf till K 5 .Därför är den icke-plan.
Om vi tar bort kanten V 2,V 7) grafen G 2 blir homeomorf till K 3.3 .Därför är det en icke-planär.
Graffärgning:
Antag att G= (V,E) är en graf utan flera kanter. En vertexfärgning av G är en tilldelning av färger till topparna av G så att intilliggande hörn har olika färger. En graf G är M-färgbar om det finns en färgning av G som använder M-färger.
Rätt färg: En färgning är korrekt om två angränsande hörn u och v har olika färger, annars kallas det felaktig färgning.
Exempel: Tänk på följande graf och färg C={r, w, b, y}. Färglägg grafen ordentligt med alla färger eller färre färger.

Grafen som visas i fig är minst 3-färgbar, därför x(G)=3
Lösning: Fig. visar grafen korrekt färgad med alla fyra färgerna.

Fig. visar grafen korrekt färgad med tre färger.

Kromatiskt antal G: Det minsta antalet färger som behövs för att producera en korrekt färgning av en graf G kallas det kromatiska antalet G och betecknas med x(G).
Exempel: Det kromatiska numret av K n är n.
Lösning: En färgning av K n kan konstrueras med n färger genom att tilldela olika färger till varje vertex. Inga två hörn kan tilldelas samma färger, eftersom varannan hörn i denna graf ligger intill varandra. Därav det kromatiska antalet K n =n.
Tillämpningar av graffärgning
Några tillämpningar av graffärgning inkluderar:
- Registerfördelning
- Karta färgläggning
- Tvådelad grafkontroll
- Mobilradiofrekvenstilldelning
- Att göra en tidtabell osv.
Ange och bevisa Handskakningssats.
Handskakningssats: Summan av grader av alla hörn i en graf G är lika med två gånger antalet kanter i grafen.
Matematiskt kan det sägas som:
∑ v∈V deg(v)=2e
Bevis: Låt G = (V, E) vara en graf där V = {v 1 ,i 2 , . . . . . . . . . .} vara uppsättningen av hörn och E = {e 1 ,Det är 2 . . . . . . . . . .} vara uppsättningen av kanter. Vi vet att varje kant ligger mellan två hörn så det ger grad ett till varje hörn. Därför bidrar varje kant med grad två för grafen. Så summan av grader av alla hörn är lika med två gånger antalet kanter i G.
Därför ∑ v∈V deg(v)=2e